|
|
|
|
|
|
|
  |
 Apr 27 2008, 01:04 AM Apr 27 2008, 01:04 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.880 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |

-------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 May 3 2008, 12:13 AM May 3 2008, 12:13 AM
Publicado:
#2
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Dejaré solamente la demostración de la convergencia, dado que el cálculo de la integral ya ha sido posteada en el foro.
Esperamos el cálculo del valor de aquella integral. |
|
|
|
 May 17 2008, 02:51 PM May 17 2008, 02:51 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.880 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
de hecho, no esperaba el calculo de la integral, si no del valor de ella
esperamos el resultado entoces pa que nos dejis postear mas ejercicios de integraleeeeeees!!!!!! jajaa saludos -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 May 19 2008, 01:52 PM May 19 2008, 01:52 PM
Publicado:
#4
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 72 Registrado: 28-April 07 Miembro Nº: 5.504 Nacionalidad:  Universidad:  Sexo:  |
de hecho esa función no tiene primitiva conocida (al menos una primitiva "normal").
Por lo tanto creo que mis conocimientos son insuficientes para calcular la integral |
|
|
|
 May 19 2008, 01:54 PM May 19 2008, 01:54 PM
Publicado:
#5
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
de hecho esa función no tiene primitiva conocida (al menos una primitiva "normal"). Así es. Hay muuuchas integrales que no poseen primitiva, pero dado que son definidas (exceptuando casos de integrales definidas que aún así no poseen valor) existen variadas técnicas para hallar su valor, y ésta, es una de ellas. Saludos y aún se espera solución para enviar este problemita a resueltos. |
|
|
|
 May 19 2008, 04:49 PM May 19 2008, 04:49 PM
Publicado:
#6
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 156 Registrado: 11-June 07 Miembro Nº: 6.615 Nacionalidad:  Sexo:  |
![TEX: $$\begin{gathered}<br /> I = \int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( x \right)} \right]dx} = \int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {2\sin \left( {\tfrac{x}<br />{2}} \right)\cos \left( {\tfrac{x}<br />{2}} \right)} \right]dx} \hfill \\<br /> I = \tfrac{\pi }<br />{2} \cdot \ln \left( 2 \right) + \int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( {\tfrac{x}<br />{2}} \right)} \right]dx} + \int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\cos \left( {\tfrac{x}<br />{2}} \right)} \right]dx} \hfill \\<br /> I\underbrace = _{u = \tfrac{x}<br />{2}}\tfrac{\pi }<br />{2} \cdot \ln \left( 2 \right) + 2 \cdot \left( {\int_0^{\tfrac{\pi }<br />{4}} {\ln \left[ {\sin \left( x \right)} \right]dx} + \int_0^{\tfrac{\pi }<br />{4}} {\ln \left[ {\cos \left( x \right)} \right]dx} } \right) \hfill \\ <br />\end{gathered} <br />$$](./tex/ba4fca7e168aab11ef9a97c09b3839d1.png) ![TEX: $$<br />{\text{Ahora notemos que:}}\int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( x \right)} \right]dx} = \int_0^{\tfrac{\pi }<br />{4}} {\ln \left[ {\sin \left( x \right)} \right]dx} + \int_0^{\tfrac{\pi }<br />{4}} {\ln \left[ {\cos \left( x \right)} \right]dx} <br />$$](./tex/e339963e70b9d7e3b2be01c785902db7.png) Luego: ![TEX: $$<br />\int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( x \right)} \right]dx} = - \tfrac{\pi }<br />{2} \cdot \ln \left( 2 \right)<br />$$](./tex/cec84821eb11b43c4e4e5704f684f6c8.png) Saludos -------------------- ![TEX: $\sqrt[3]{\displaystyle\sum_{i=1}^n{i^{3\cdot{\sqrt[]{3}}-1}}}\approx{\displaystyle\sum_{i=1}^n{i^{\sqrt[]{3}-1}}}$](./tex/1187710902.gif) |
|
|
|
 May 30 2008, 03:21 PM May 30 2008, 03:21 PM
Publicado:
#7
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 156 Registrado: 11-June 07 Miembro Nº: 6.615 Nacionalidad:  Sexo:  |
Otra prueba
![TEX: $$<br />\begin{gathered}<br /> {\text{Consideremos la identidad:}} \hfill \\<br /> - \ln \left[ {2 \cdot \sin \left( {\tfrac{x}<br />{2}} \right)} \right] = \sum\limits_{k = 1}^{ + \infty } {\tfrac{{\cos \left( {k \cdot x} \right)}}<br />{k}} {\text{ v\'a lida cuando }}0 < x < \pi \hfill \\<br /> {\text{Integrando tenemos:}} \hfill \\<br /> - \ln \left( 2 \right) \cdot \pi - \int_0^\pi {\ln \left[ {\sin \left( {\tfrac{x}<br />{2}} \right)} \right]dx} = \sum\limits_{k = 1}^{ + \infty } {\tfrac{1}<br />{k} \cdot \int_0^\pi {\cos \left( {k \cdot x} \right)dx} } = \sum\limits_{k = 1}^{ + \infty } {\tfrac{{\sin \left( {k \cdot \pi } \right)}}<br />{{k^2 }} = 0} \hfill \\<br /> {\text{Luego:}} \hfill \\<br /> \int_0^\pi {\ln \left[ {\sin \left( {\tfrac{x}<br />{2}} \right)} \right]dx} = - \ln \left( 2 \right) \cdot \pi \underbrace \Rightarrow _{u = \tfrac{x}<br />{2}}\int_0^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( u \right)} \right]du} = - \tfrac{\pi }<br />{2} \cdot \ln \left( 2 \right) \hfill \\ <br />\end{gathered} <br />$$](./tex/3fd7fc18c3a0036401cae6ad4a0297e2.png) Saludos -------------------- ![TEX: $\sqrt[3]{\displaystyle\sum_{i=1}^n{i^{3\cdot{\sqrt[]{3}}-1}}}\approx{\displaystyle\sum_{i=1}^n{i^{\sqrt[]{3}-1}}}$](./tex/1187710902.gif) |
|
|
|
 Oct 9 2008, 05:08 PM Oct 9 2008, 05:08 PM
Publicado:
#8
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 156 Registrado: 11-June 07 Miembro Nº: 6.615 Nacionalidad:  Sexo:  |
![TEX: $$<br />\begin{gathered}<br /> {\text{Dado }}x \in \left( {0,\tfrac{\pi }<br />{2}} \right){\text{ tenemos:}} \hfill \\<br /> \log \left[ {\sin \left( x \right)} \right] = \tfrac{1}<br />{2} \cdot \log \left[ {1 - \cos ^2 \left( x \right)} \right] = - \tfrac{1}<br />{2} \cdot \left( {\sum\limits_{k = 1}^\infty {\tfrac{{\cos ^{2k} \left( x \right)}}<br />{k}} } \right) \hfill \\<br /> \int_0^{\tfrac{\pi }<br />{2}} {\log \left[ {\sin \left( x \right)} \right]dx} = - \tfrac{1}<br />{2} \cdot \int_0^{\tfrac{\pi }<br />{2}} {\left( {\sum\limits_{k = 1}^\infty {\tfrac{{\cos ^{2k} \left( x \right)}}<br />{k}} } \right)dx} = - \tfrac{1}<br />{2} \cdot \sum\limits_{k = 1}^\infty {\left( {\tfrac{1}<br />{k} \cdot \int_0^{\tfrac{\pi }<br />{2}} {\cos ^{2k} \left( x \right)dx} } \right)} \hfill \\<br /> {\text{Recordemos que:}}{\text{ }}\int_0^{\tfrac{\pi }<br />{2}} {\cos ^{2k} \left( x \right)dx} = \binom{2k}{k} \cdot \tfrac{\pi }<br />{{2^{2k + 1} }} \hfill \\<br /> {\text{Luego}}:\int_0^{\tfrac{\pi }<br />{2}} {\log \left[ {\sin \left( x \right)} \right]dx} = - \tfrac{\pi }<br />{4} \cdot \sum\limits_{k = 1}^\infty {\binom{2k}{k} \cdot \tfrac{1}<br />{{4^k \cdot k}}} \hfill \\<br /> {\text{Ahora:}}{\text{ }}\sum\limits_{k = 0}^\infty {\binom{2k}{k} \cdot z^k } = \tfrac{1}<br />{{\sqrt {1 - 4z} }} \Rightarrow \sum\limits_{k = 1}^\infty {\binom{2k}{k} \cdot \tfrac{1}<br />{{4^k \cdot k}}} = \int_0^1 {\left( {\tfrac{1}<br />{{\sqrt {1 - z} }} - 1} \right) \cdot \tfrac{1}<br />{z}dz} \hfill \\<br /> \int_0^1 {\left( {\tfrac{1}<br />{{\sqrt {1 - z} }} - 1} \right) \cdot \tfrac{1}<br />{z}dz} = \int_0^1 {\tfrac{{1 - \sqrt {1 - z} }}<br />{{z \cdot \sqrt {1 - z} }}dz} = \int_0^1 {\tfrac{{dz}}<br />{{\left( {1 + \sqrt {1 - z} } \right) \cdot \sqrt {1 - z} }}} \underbrace = _{u = 1 + \sqrt {1 - z} }2 \cdot \int_1^2 {\tfrac{{du}}<br />{u}} = 2 \cdot \log \left( 2 \right) \hfill \\<br /> \therefore \int_0^{\tfrac{\pi }<br />{2}} {\log \left[ {\sin \left( x \right)} \right]dx} = - \tfrac{\pi }<br />{2} \cdot \log \left( 2 \right) \hfill \\ <br />\end{gathered} <br />$$](./tex/30d755492b3138ed5f11d923be542280.png) Saludos -------------------- ![TEX: $\sqrt[3]{\displaystyle\sum_{i=1}^n{i^{3\cdot{\sqrt[]{3}}-1}}}\approx{\displaystyle\sum_{i=1}^n{i^{\sqrt[]{3}-1}}}$](./tex/1187710902.gif) |
|
|
|
 Sep 17 2021, 11:14 PM Sep 17 2021, 11:14 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.880 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Mi primer propuesto... que nostalgia....
Para el calculo de la integral, vamos a notar lo siguiente: 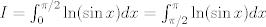 , por lo tanto , por lo tanto 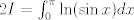 Como el seno es positivo en dicho intervalo, utilizaremos esta reversión de la clásica identidad: 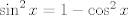 como como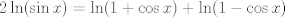 valido si valido si ![TEX: $x \in ]0,\pi[$](/tex-image/b1307d689cfb6790d6d243c4088dc973.png) Por otro lado notaremos que $-\ln(1-re^{i\theta})=\sum_{n=1}^{\infty}\frac{r^ne^{in \theta}}{n}$ (ojo, es la ramificación principal del logaritmo) Por lo que usando que 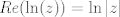 y que y que 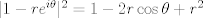 al tomar parte real: al tomar parte real: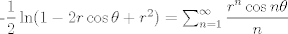 Es facil ver que el limite cuando 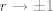 las series siguen siendo convergente (por eso se excluyen los puntos en que es 0 y las series siguen siendo convergente (por eso se excluyen los puntos en que es 0 y  y tenemos que 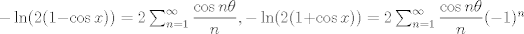 Lo que significa que sumando: 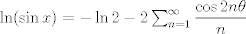 (ver segunda prueba de PaulRS) (ver segunda prueba de PaulRS)Ahora, esta es una serie de fourier con 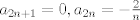 y y 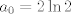 . Por lo tanto notemos que: . Por lo tanto notemos que: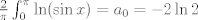 y por lo tanto y por lo tanto 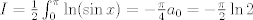 Saludos Claudio. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th October 2025 - 04:46 PM |





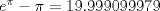
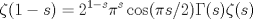






![TEX: \textsf{Lema. $\displaystyle\int_0^a\ln x\,dx$ converge $\forall\,a\in\mathbb R^+.$\\\\\underline{Demostración}. Después de definir $x\to\dfrac xa$ tenemos:$$\int_{0}^{a}{\ln x\,dx}=a\left\{ \int_{0}^{1}{\ln x\,dx}+\ln a \right\}=a(\ln a-1).\quad\blacksquare$$\indent Por otra parte, tenemos que $\dfrac{2x}{\pi }\le \operatorname{sen}x\le x$ para $0\le x\le\dfrac\pi2.$ Finalmente$$\int_{0}^{\pi /2}{\ln \left( \frac{2x}{\pi } \right)\,dx}\le \int_{0}^{\pi /2}{\ln (\operatorname{sen}x)\,dx}\le \int_{0}^{\pi /2}{\ln x\,dx},$$\noindent y dada la monotonía de $\ln (\operatorname{sen}x)$ en $\bigg[ 0,\dfrac{\pi }{2} \bigg]$ establecemos la convergencia de la integral dada.$\quad\blacksquare$}](./tex/c9ed3fabc6f37101b89a39667f4166c3.png)

![TEX: $$<br />{\text{Basta hacer: }}u = \tfrac{\pi }<br />{2} - x \Rightarrow \int_0^{\tfrac{\pi }<br />{4}} {\ln \left[ {\cos \left( x \right)} \right]dx = } \int_{\tfrac{\pi }<br />{4}}^{\tfrac{\pi }<br />{2}} {\ln \left[ {\sin \left( x \right)} \right]dx} <br />$$](./tex/c46a7d04f22e4bd82d01d10b21f67539.png)