C2 Geometría - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

C2 Geometría, MAT1102 1S 2008

Opciones

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 25 2008, 08:37 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{center}<br />MAT1102 - Geometría\\<br />Control 2 - Martes 22 de Abril de 2008 - Fila A\end{center}<br />\begin{enumerate}<br />\item Demuestre sin calculadora que \[\arcsin\left(\dfrac{3}{5}\right) + \arcsin\left(\dfrac{8}{17}\right)+\arcsin\left(\dfrac{36}{85}\right)=\dfrac{\pi}{2}\]<br />\item Resuelva la ecuación:<br />\[\arcsin{x}-\arccos{x}=\arcsin{(3x-2)}\]<br />\item Resuelva la ecuación:<br />\[\cos{(3\theta)}=\cos{(5\theta)}+\sqrt{3}\sin{(4\theta)}\]<br />\end{enumerate}<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2008, 01:02 PM Publicado: #2
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	veamos como me va, hace tiempo que no resuelvo una ecuacion trigonometrica: $TEX: \[<br />\begin{gathered}<br /> \cos 3\theta = \cos 5\theta + \sqrt 3 \sin 4\theta \hfill \\<br /> \cos 5\theta - \cos 3\theta + \sqrt 3 \sin 4\theta = 0 \hfill \\<br /> \hfill \\<br /> {\text{conociendo la identidad: }}\cos x - \cos y = - 2\sin \left( {\frac{{x + y}}<br />{2}} \right)\sin \left( {\frac{{x - y}}<br />{2}} \right) \hfill \\<br /> \hfill \\<br /> - 2\sin \left( {\frac{{5\theta + 3\theta }}<br />{2}} \right)\sin \left( {\frac{{5\theta - 3\theta }}<br />{2}} \right) + 2 \cdot \frac{{\sqrt 3 }}<br />{2}\sin 4\theta = 0 \hfill \\<br /> \hfill \\<br /> - 2\sin 4\theta \cdot \sin \theta + 2\sin \left( {\frac{\pi }<br />{3}} \right)\sin 4\theta = 0 \hfill \\<br /> \sin 4\theta \cdot \sin \theta - \sin \left( {\frac{\pi }<br />{3}} \right)\sin 4\theta = 0 \hfill \\<br /> \sin 4\theta \left( {\sin \theta - \sin \left( {\frac{\pi }<br />{3}} \right)} \right) = 0 \hfill \\<br /> \hfill \\<br /> {\text{Primer caso:}} \hfill \\<br /> \sin 4\theta = 0/\arcsin () \hfill \\<br /> 4\theta = 0 \Leftrightarrow \theta = 0 \hfill \\<br /> {\text{pero en general seria: }}\theta = k\pi ;\forall k \in \mathbb{Z} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> {\text{Segundo caso:}} \hfill \\<br /> \sin \theta = \sin \left( {\frac{\pi }<br />{3}} \right)/\arcsin () \hfill \\<br /> \theta = \frac{\pi }<br />{3} \hfill \\<br /> {\text{pero en general seria: }}\theta = \frac{\pi }<br />{3} + 2k\pi ;\forall k \in \mathbb{Z} \hfill \\<br /> \hfill \\<br /> {\text{Ahora yo veo un tercer caso}}{\text{, ya que }}\sin \left( {\frac{\pi }<br />{3}} \right) = \sin \left( {\frac{{2\pi }}<br />{3}} \right),{\text{ entonces:}} \hfill \\<br /> {\text{Tercer caso:}} \hfill \\<br /> \theta = \frac{{2\pi }}<br />{3} \hfill \\<br /> {\text{en general seria: }}\theta = \frac{{2\pi }}<br />{3} + 2k\pi ;\forall k \in \mathbb{Z} \hfill \\<br /> \hfill \\<br /> \therefore {\text{Las soluciones serian:}}\left( {\forall k \in \mathbb{Z}} \right) \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\boxed{\theta = k\pi \wedge \theta = \frac{\pi }<br />{3} + 2k\pi \wedge \theta = \frac{{2\pi }}<br />{3} + 2k\pi }<br />\]<br />$ saludos -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 5 2008, 10:22 PM Publicado: #3
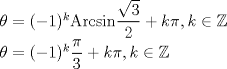
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Sólo agregar que para resolver senos, sería más cómodo utilizar: $TEX: $\\<br />\theta = (-1)^k \text{Arcsin}\dfrac{\sqrt{3}}{2}+k\pi, k\in\mathbb{Z}\\<br />\theta = (-1)^k\dfrac{\pi}{3} +k\pi, k\in\mathbb{Z}$$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

« Posterior · Geometría · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 10th April 2025 - 11:52 AM