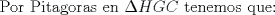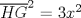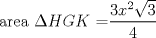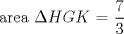|
|
|
|
|
|
|
  |
 Apr 23 2008, 08:27 PM Apr 23 2008, 08:27 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Para que completemos esta sección les pido que posteen los problemas que faltan ya que no pude cosegirlos. Tampoco se cual número corresponde a cual. Bueno este es el problema que me tocó a mi:
  ( El enunciado no es exactamente el mismo pero el problema en sí si lo es )  ![TEX: <br />Calcular el valor exacto de:\[<br />\frac{{1 \times 4}}<br />{{2 \times 3}} + \frac{{2 \times 5}}<br />{{3 \times 4}} + \frac{{3 \times 6}}<br />{{4 \times 5}} + ... + \frac{{100 \times 103}}<br />{{101 \times 102}}<br />\]<br />](./tex/6ad46f668399128094a8a192cb38f9f3.png) 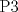 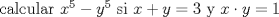 con x > y 
Mensaje modificado por Nilrem el Apr 25 2008, 10:00 PM
Archivo(s) Adjunto(s)
|
|
|
|
 Apr 23 2008, 08:38 PM Apr 23 2008, 08:38 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
este problema estaba en tu prueba?
esq io la tendi en la IX region es la misma? esq si es por eso recuerdo un par de problemas de la prueba jejeje -------------------- |
|
|
|
 Apr 23 2008, 08:53 PM Apr 23 2008, 08:53 PM
Publicado:
#3
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Si ese si estaba , audame con los otros problemas noma
|
|
|
|
 Apr 23 2008, 09:08 PM Apr 23 2008, 09:08 PM
Publicado:
#4
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
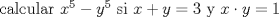 con x>y Mensaje modificado por Versuchung el Apr 23 2008, 11:09 PM -------------------- |
|
|
|
 Apr 23 2008, 09:18 PM Apr 23 2008, 09:18 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- asdf
|
|
|
|
 Apr 23 2008, 09:25 PM Apr 23 2008, 09:25 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 399 Registrado: 14-August 07 Desde: Temuco Miembro Nº: 8.739 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
ouch no recuerdo en este momento...
:S -------------------- |
|
|
|
 Apr 23 2008, 10:22 PM Apr 23 2008, 10:22 PM
Publicado:
#7
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 329 Registrado: 24-August 06 Desde: Concepción Miembro Nº: 2.038 Nacionalidad:  Colegio/Liceo:  Sexo:  |
 PD: era x>y en el que puso versuchung. Mensaje modificado por Manuel71 el Apr 23 2008, 10:25 PM |
|
|
|
 Apr 23 2008, 10:26 PM Apr 23 2008, 10:26 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 122 Registrado: 6-October 06 Desde: VIII Región Miembro Nº: 2.438 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
|
|
|
|
 Apr 23 2008, 10:33 PM Apr 23 2008, 10:33 PM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Un detalle... debiste decir que los triangulos son congruentes Saludos |
|
|
|
 Apr 23 2008, 11:12 PM Apr 23 2008, 11:12 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
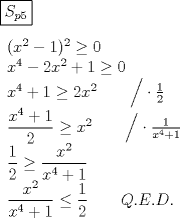 No hay problema en multiplicar la desigualdad por 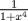 ya que este número siempre es positivo, por lo que la desigualdad no cambia de sentido ya que este número siempre es positivo, por lo que la desigualdad no cambia de sentido---------------------------------------------------------------------------------------------------------------------------------- El problema de las potencias quintas creo que debería ser 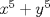 para hacerlo de la forma "elegante". Pero como era así el problema saqué el valor de "x" y de "y", los elevé a la quinta y los resté xD y me dio para hacerlo de la forma "elegante". Pero como era así el problema saqué el valor de "x" y de "y", los elevé a la quinta y los resté xD y me dio 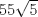 Y el problema de trigonometria no supe demostrarlo, sólo pusimos que la suma era máxima cuando el seno y el coseno eran iguales y que esto se producía cuando 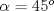 y la suma daba y la suma daba 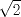 Salu2 --------------------     |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:14 PM |


















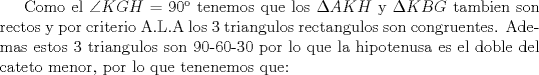
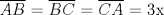
![TEX: \[7 = \frac{{(3x)^2 \sqrt 3 }}{4}\]](./tex/64496fceeaf3f0965232b1ebd3c1f7f8.png)
![TEX: \[x^2 = \frac{{28}}{{9\sqrt 3 }}\]](./tex/7fa25f281ebea964f795a44a037680ec.png)