Relaciones entre áreas y bases - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Geometría > Teoremas y Formulas

2 Páginas:

< 1 2

Reply to this topic

Start new topic

Relaciones entre áreas y bases, a pedido de Kenshin

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 14 2006, 03:02 PM Publicado: #11
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Kenshin @ Jul 14 2006, 01:17 AM) 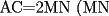$TEX: AC=2MN (MN$ es mediana) ¿Y la demostracion de esta afirmacion (o sea porque el ser la union de los puntos medios implica esa relacion)? PD: Es solo para que la demostracion quede completa Me gustaría dar una explicación alternativa a la de Krizalid, para decir realmente que esa aseveración es cierta. 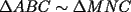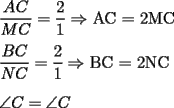screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img157.imageshack.us/img157/6397/mnmediana5fg.th.png');}" /> $TEX: $\Delta ABC\sim\Delta MNC$$ , pues $TEX: $\dfrac{AC}{MC}=\dfrac{2}{1}\Rightarrow$ AC = 2MC \\ <br /><br />$\dfrac{{BC}}{{NC}}=\dfrac{2}{1}\Rightarrow$ BC = 2NC \\ <br /><br />$\angle C = \angle C$$ (ángulo común) Entonces, tenemos que: 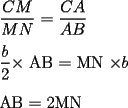$TEX: $\dfrac{CM}{MN}$ = $\dfrac{CA}{AB}$ \\ <br /><br />$\dfrac{b}{2} \times$ AB = MN $\times b$ \\ <br /><br />AB = 2MN$ ------- Edited, me había olvidado de poner la imagen --------------------

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2007, 02:29 PM Publicado: #12
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	CITA(Killua @ Feb 21 2006, 04:02 PM) Teorema de Van Obel* screen.width0.6) {this.resized=true; this.width=screen.width0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaÃ±o original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img467.imageshack.us/img467/6554/tabel9rv.png');}" /> No tengo ánimos para dibujar así que tomaré prestada esta imagen 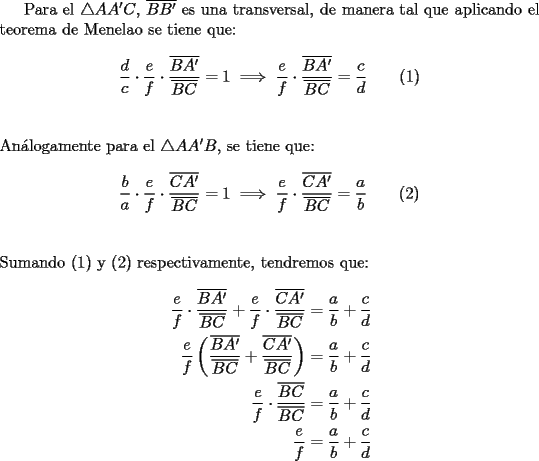$TEX: Para el $\triangle AA'C$, $\overline {BB'}$ es una transversal, de manera tal que aplicando el teorema de Menelao se tiene que:<br /><br />$$\dfrac{d}<br />{c} \cdot \dfrac{e}<br />{f} \cdot \dfrac{{\overline {BA'} }}<br />{{\overline {BC} }} = 1 \implies \dfrac{e}<br />{f} \cdot \dfrac{{\overline {BA'} }}<br />{{\overline {BC} }} = \dfrac{c}<br />{d}\qquad (1)$$\\<br /><br />\noindent An\'alogamente para el $\triangle AA'B$, se tiene que:<br /><br />$$\dfrac{b}<br />{a} \cdot \dfrac{e}<br />{f} \cdot \dfrac{{\overline {CA'} }}<br />{{\overline {BC} }} = 1 \implies \dfrac{e}<br />{f} \cdot \dfrac{{\overline {CA'} }}<br />{{\overline {BC} }} = \dfrac{a}<br />{b}\qquad (2)$$\\<br /><br />\noindent Sumando (1) y (2) respectivamente, tendremos que:<br /><br />\begin{equation}<br />\begin{aligned}<br /> \frac{e}<br />{f} \cdot \frac{{\overline {BA'} }}<br />{{\overline {BC} }} + \frac{e}<br />{f} \cdot \frac{{\overline {CA'} }}<br />{{\overline {BC} }} &= \frac{a}<br />{b} + \frac{c}<br />{d} \hfill \\<br /> \frac{e}<br />{f}\left( {\frac{{\overline {BA'} }}<br />{{\overline {BC} }} + \frac{{\overline {CA'} }}<br />{{\overline {BC} }}} \right) &= \frac{a}<br />{b} + \frac{c}<br />{d} \hfill \\<br /> \frac{e}<br />{f} \cdot \frac{{\overline {BC} }}<br />{{\overline {BC} }} &= \frac{a}<br />{b} + \frac{c}<br />{d} \hfill \\<br /> \frac{e}<br />{f} &= \frac{a}<br />{b} + \frac{c}<br />{d} \hfill \\ <br />\end{aligned}<br />\end{equation}$ P.D.: yo conocía este teorema con el nombre de Van Obel , me es ignota la información del nombre por ahora

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 4 2007, 01:18 AM Publicado: #13
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Krizalid @ Jan 8 2007, 04:29 PM) P.D.: yo conocía este teorema con el nombre de Van Obel , me es ignota la información del nombre por ahora Ciertamente, en el Verano Matemático de la UdeC lo pasaron como teorema de Van Aubel Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

Killua Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 4 2007, 01:28 AM Publicado: #14
Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Bueeeeeno, no importa como se llame, dejémoslo como teorema -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy) "A mathematician is a device for turning coffee into theorems" (Paul Erdös)

el_andreslda Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 8 2013, 10:46 PM Publicado: #15
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 11-September 11 Desde: Rancagua Miembro Nº: 94.201 Nacionalidad: Universidad: Sexo:	Revivo este tema porque debo demostrar lo de las transversales de gravedad que estan en razon 2:1, quería saber como era, pero varias imagenes no estan porfa si alguien puede ayudarme o darme un empujoncito --------------------

pablo gauss Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 9 2013, 04:00 PM Publicado: #16
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.374 Registrado: 3-January 13 Desde: Santiago Miembro Nº: 114.680 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(el_andreslda @ Oct 8 2013, 11:46 PM) Revivo este tema porque debo demostrar lo de las transversales de gravedad que estan en razon 2:1, quería saber como era, pero varias imagenes no estan porfa si alguien puede ayudarme o darme un empujoncito mira ese triangulo cualquiera ABC , trazamos las medianas CD y AE ,el punto de intersección de ambas rectas necesariamente es el baricentro,luego trazamos la recta EH paralela a CD, CE y EB están en la razón 1:1,por thales DH Y HB estan en la misma razón..,ahora finaliza aplicando el mismo razonamiento con los triangulos ADB Y AHE ,con B ., como baricentro. Mensaje modificado por pablo gauss el Oct 9 2013, 04:07 PM Archivo(s) Adjunto(s) TRIA.PNG ( 9.39k ) Número de descargas: 3 -------------------- Mi nombre es Juan Pablo ஸ்ரீனிவாஸ ஐயங்கார் ராமானுஜன் "Parece bastante enfermo, pero sobre todo se aprecia el genio que era" $TEX: \[<br />\pi = \left( {\frac{{\sqrt 8 }}<br />{{9801}}\sum\limits_{n = 0}^\infty {\frac{{\left( {4n} \right)!(1103 + 26390n)}}<br />{{(n!)^4 396^{4n} }}} } \right)^{ - 1} <br />\]<br />$ “Yo soy un trabajador de la música, no soy un artista. El pueblo y el tiempo dirán si yo soy artista. Yo, en este momento, soy un trabajador. Y un trabajador que está ubicado con conciencia muy definida.” ―Víctor Jara [color="#0000FF"][/color]

« Posterior · Teoremas y Formulas · Anterior »

2 Páginas:

< 1 2

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:52 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.