|
|
|
|
|
|
|
  |
 Feb 19 2006, 10:59 PM Feb 19 2006, 10:59 PM
Publicado:
#1
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Propiedad 1
Bueno, esta propiedad nos dice que las áreas de los triángulos de igual altura son proporcionales a las bases de los triángulos. O sea: 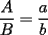 , donde , donde 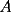 y y 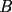 son las áreas de los triángulos, y son las áreas de los triángulos, y  y y 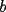 las bases. las bases. screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img135.imageshack.us/img135/3528/a2le.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img135.imageshack.us/img135/3528/a2le.png');}" />Demostración:  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img135.imageshack.us/img135/5076/aa7hi.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img135.imageshack.us/img135/5076/aa7hi.png');}" />Esta propiedad es utilizada para probar el Teorema de Ceva y las propiedades de las transversales de gravedad, entre otras cosas. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Feb 20 2006, 04:32 PM Feb 20 2006, 04:32 PM
Publicado:
#2
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Propiedad 2
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img108.imageshack.us/img108/7917/abcd5hl.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img108.imageshack.us/img108/7917/abcd5hl.png');}" />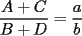 Donde 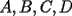 son las áreas de los triángulos son las áreas de los triángulos 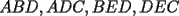 , respectivamente; , respectivamente;  y y 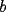 son los segmentos son los segmentos 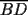 y y 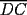 , respectivamente. , respectivamente.Demostración: -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Feb 20 2006, 05:00 PM Feb 20 2006, 05:00 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Ejemplo:
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img304.imageshack.us/img304/2066/p11sc.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img304.imageshack.us/img304/2066/p11sc.png');}" />Pruebe que: 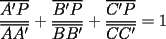 Solución: -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Feb 20 2006, 08:25 PM Feb 20 2006, 08:25 PM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Mas que excelente aporte...mejor de lo que yo esperaba para alguien que recien esta pasando a primero medio
Solo un detalle, y es que en el Ejemplo, cuando lo aplicas, no es exactamente la propiedad 2, pero es basicamente la misma idea. Mis saludos y felicitaciones -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 21 2006, 02:02 PM Feb 21 2006, 02:02 PM
Publicado:
#5
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Y continúa...
Propiedad 3 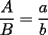 (ver figura) (ver figura) screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img310.imageshack.us/img310/8601/pr33eu.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img310.imageshack.us/img310/8601/pr33eu.png');}" />Demostración: Teorema  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img467.imageshack.us/img467/6554/tabel9rv.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img467.imageshack.us/img467/6554/tabel9rv.png');}" />En un triángulo con un set de cevianas concurrentes (ver figura), se cumple que: 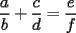 Donde: 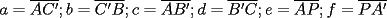 Demostración: -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Feb 22 2006, 03:50 PM Feb 22 2006, 03:50 PM
Publicado:
#6
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Propiedades de las transversales de gravedad
Propiedad 1: "Al trazar las tres transversales de gravedad en un triangulo cualquiera este queda dividido en seis triangulos de la misma área"  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img138.imageshack.us/img138/5968/trian7ah.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img138.imageshack.us/img138/5968/trian7ah.png');}" />Demostración: Propiedad 2: Las transversales de gravedad de un triángulo se dividen entre sí en la razón 2:1. Demostración: De todo esto podemos sacar una: Conclusión: En general, las bases de un triángulo son proporcionales al área, a la suma de las áreas y a la diferencia de el(las) área(s) que abarca(n). Eso sería todo... si alguien quiere aportar con algún ejemplo en que se utilicen estas propiedades, una demostración, bienvenido sea Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Apr 29 2006, 06:14 AM Apr 29 2006, 06:14 AM
Publicado:
#7
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 13-April 06 Miembro Nº: 841 |
¿Y qué hay del recíproco? Es decir, si tenés tres cevianas que dividen al triángulo en seis triángulos de igual área, puedes afirmar que el punto de concurrencia es el baricentro?
|
|
|
|
 Jul 13 2006, 03:55 PM Jul 13 2006, 03:55 PM
Publicado:
#8
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Bueno, yo quiero compatir otra demostración acerca de la razón en la cual se cortan las transversales de gravedad.
Consideremos la siguiente ilustración:  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img153.imageshack.us/img153/6305/tri9wf.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img153.imageshack.us/img153/6305/tri9wf.png');}" />En la figura se tiene un ![TEX: \[<br />\Delta ABC<br />\]](./tex/88703.gif) . Se trazan las transversales de gravedad . Se trazan las transversales de gravedad ![TEX: \[<br />\overline {CM} <br />\]](./tex/88704.gif) y y ![TEX: \[<br />\overline {AN} <br />\]](./tex/88705.gif) Construcción auxiliar. Trazamos la mediana ![TEX: \[<br />\overline {MN} <br />\]](./tex/88706.gif) . .Tesis: ![TEX: \[<br />\frac{{\overline {CG} }}<br />{{\overline {GM} }} = \frac{{\overline {AG} }}<br />{{\overline {GN} }} = 2.<br />\]](./tex/88707.gif) Demostración: ![TEX: \[<br />\Delta ACG \sim \Delta NMG<br />\]](./tex/88708.gif) (por tener sus tres ángulos iguales) (por tener sus tres ángulos iguales)![TEX: \[<br />\therefore {\text{ }}\frac{{\overline {CG} }}<br />{{\overline {GM} }} = \frac{{\overline {AG} }}<br />{{\overline {GN} }} = \frac{{\overline {AC} }}<br />{{\overline {MN} }}<br />\]](./tex/88709.gif) Pero: ![TEX: \[<br />\overline {AC} = 2\overline {MN} <br />\]](./tex/88710.gif) ( (![TEX: \[<br />\overline {MN} <br />\]](./tex/88711.gif) es mediana) es mediana)Obteniendo así: ![TEX: \[<br />\frac{{\overline {CG} }}<br />{{\overline {GM} }} = \frac{{\overline {AG} }}<br />{{\overline {GN} }} = 2.<br />\]](./tex/88712.gif) Como queríamos demostrar. |
|
|
|
 Jul 14 2006, 12:17 AM Jul 14 2006, 12:17 AM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
CITA ![TEX: \[<br />\overline {AC} = 2\overline {MN} <br />\]](./tex/88710.gif) ( (![TEX: \[<br />\overline {MN} <br />\]](./tex/88711.gif) es mediana) es mediana)¿Y la demostracion de esta afirmacion (o sea porque el ser la union de los puntos medios implica esa relacion)? Saludos PD: Es solo para que la demostracion quede completa -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jul 14 2006, 12:39 PM Jul 14 2006, 12:39 PM
Publicado:
#10
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Siendo este, mi post 400 en este espectacular foro, deleitaré a mis paizanos con esta demostración:
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img176.imageshack.us/img176/7929/med3lg.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img176.imageshack.us/img176/7929/med3lg.png');}" />En la figura: ![TEX: \[<br />\Delta ABC<br />\]](./tex/89375.gif) donde donde ![TEX: \[<br />M<br />\]](./tex/89376.gif) y y ![TEX: \[<br />N<br />\]](./tex/89377.gif) son los puntos medios de son los puntos medios de ![TEX: \[<br />\overline {AC} <br />\]](./tex/89378.gif) y y ![TEX: \[<br />\overline {BC} <br />\]](./tex/89379.gif) "La mediana, es el trazo que une dos puntos medios de un triángulo que a su vez es paralela al tercer lado e igual a su mitad". Tesis: ![TEX: \[<br />\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}<br />\]](./tex/89380.gif) ; ; ![TEX: \[<br />\overline {MN} = \frac{{\overline {AB} }}<br />{2}<br />\]](./tex/89381.gif) Construcción auxiliar. Por ![TEX: \[<br />N<br />\]](./tex/89382.gif) tracemos tracemos ![TEX: \[<br />\overleftrightarrow {PN}\parallel \overleftrightarrow {AC}<br />\]](./tex/89383.gif) , dando origen así al , dando origen así al ![TEX: \[<br />\Delta BNP<br />\]](./tex/89384.gif) . .Demostración: ![TEX: \[<br />\frac{{\overline {CM} }}<br />{{\overline {MA} }} = 1<br />\]](./tex/89385.gif) (por ser (por ser ![TEX: \[<br />M<br />\]](./tex/89386.gif) punto medio, por tanto punto medio, por tanto ![TEX: \[<br />\overline {CM} = \overline {MA} <br />\]](./tex/89387.gif) ) (1) ) (1)![TEX: \[<br />\frac{{\overline {CN} }}<br />{{\overline {NB} }} = 1<br />\]](./tex/89388.gif) (por ser (por ser ![TEX: \[<br />N<br />\]](./tex/89389.gif) punto medio, por tanto punto medio, por tanto ![TEX: \[<br />\overline {CN} = \overline {NB} <br />\]](./tex/89390.gif) ) (2) ) (2)Comparando (1) y (2): ![TEX: \[<br />\frac{{\overline {CM} }}<br />{{\overline {MA} }} = \frac{{\overline {CN} }}<br />{{\overline {NB} }}<br />\]](./tex/89391.gif) ![TEX: \[<br />\therefore {\text{ }}\overleftrightarrow {MN}\parallel \overleftrightarrow {AB}<br />\]](./tex/89392.gif) (cuando una recta al cortar dos lados de un triángulo los divide en segmentos proporcionales, la recta es paralela al tercer lado) (cuando una recta al cortar dos lados de un triángulo los divide en segmentos proporcionales, la recta es paralela al tercer lado)En los ![TEX: \[<br />\Delta CMN<br />\]](./tex/89393.gif) y y ![TEX: \[<br />\Delta NPB<br />\]](./tex/89394.gif) : :![TEX: \[<br />\angle {\text{ }}C = \angle {\text{ }}1<br />\]](./tex/89395.gif) , , ![TEX: \[<br />\angle {\text{ }}B = \angle {\text{ }}2<br />\]](./tex/89396.gif) (correspondientes entre paralelas) (correspondientes entre paralelas)![TEX: \[<br />\overline {CN} = \overline {NB} <br />\]](./tex/89397.gif) (por ser (por ser ![TEX: \[<br />N<br />\]](./tex/89398.gif) punto medio) punto medio)![TEX: \[<br />\therefore {\text{ }}\Delta CMN \cong \Delta NPB<br />\]](./tex/89399.gif) (criterio ALA) (criterio ALA)![TEX: \[<br />\therefore {\text{ }}\overline {MN} = \overline {PB} <br />\]](./tex/89400.gif) (lados homólogos de los triángulos iguales) (3) (lados homólogos de los triángulos iguales) (3)Por otra parte: ![TEX: \[<br />\overline {MN} = \overline {AP} <br />\]](./tex/89401.gif) (lados opuestos de un paralelógramo) (4) (lados opuestos de un paralelógramo) (4)![TEX: \[<br />AMNP<br />\]](./tex/89402.gif) es un paralelógramo, se puede demostrar trazando la diagonal es un paralelógramo, se puede demostrar trazando la diagonal ![TEX: \[<br />\overline {AN} <br />\]](./tex/89403.gif) para afirmar que para afirmar que ![TEX: \[<br />\overline {MN} = \overline {AP} <br />\]](./tex/89404.gif) . .Sumando (3) y (4): 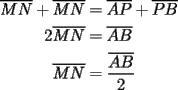 Como queríamos demostrar. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:07 PM |






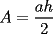 y
y 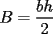
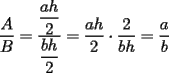



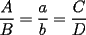
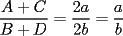
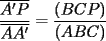 (propiedad 2)
(propiedad 2)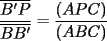 (propiedad 2)
(propiedad 2)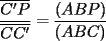 (propiedad 2)
(propiedad 2)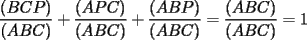
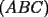 significa "área del triángulo ABC"
significa "área del triángulo ABC"
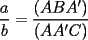 (propiedad 1)
(propiedad 1)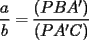 (propiedad 1)
(propiedad 1)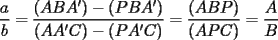
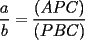 (propiedad 3)
(propiedad 3)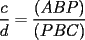 (propiedad 3)
(propiedad 3)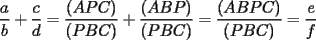 (esto último por la propiedad 2)
(esto último por la propiedad 2)
 screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img142.imageshack.us/img142/175/trian7ah0mw.png');}" />
screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img142.imageshack.us/img142/175/trian7ah0mw.png');}" />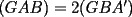 (propiedad 1 transversales de gravedad). Y por propiedad 1 (las áreas son proporcionales a sus bases)
(propiedad 1 transversales de gravedad). Y por propiedad 1 (las áreas son proporcionales a sus bases) 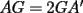 . Del mismo modo,
. Del mismo modo, 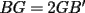 , y
, y