|
|
|
|
|
|
|
  |
 Feb 14 2006, 02:02 PM Feb 14 2006, 02:02 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Tema 1. Introduccion.
1.1 Objetivos: seamos honestos... la idea de muchos de los que lean la guia no sera aprender sino salvar la PSU, asi que diremos que el objetivo de la guia es poder defendernos en por lo menos este tema en la PSU de matematicas. 1.2 Que es un sistema de ecuaciones? Un sistema de ecuaciones consiste en 2 o mas ecuaciones de 2 o mas incognitas. En particular, diremos que el sistema es de 2x2 si consiste en 2 ecuaciones con 2 incognitas, y de 3x3 si consiste en 3 ecuaciones con 3 incognitas. En adelante nuestras incognitas seran designadas por las ultimas letras del alfabeto a menos que se indique lo contrario. Ejemplo 1.2.1 Sistema 2x2 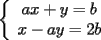 Tenemos 2 incognitas,  e e 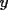 , mientras que , mientras que 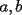 son coeficientes literales que suponemos conocidos (podrian ser numeros, pero resolver con esos factores literales nos da la solucion general para esa forma del sistema). Hay 2 ecuacion y 2 incognitas, es decir, el sistema es de 2x2. son coeficientes literales que suponemos conocidos (podrian ser numeros, pero resolver con esos factores literales nos da la solucion general para esa forma del sistema). Hay 2 ecuacion y 2 incognitas, es decir, el sistema es de 2x2.Ejemplo 1.2.2 Sistema 3x3 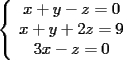 Notemos que la tercera ecuacion del sistema tiene 2 incognitas, pero en total entre las 3 ecuaciones contamos 3 incognitas y el sistema es de 3x3 1.3 Que significa resolver un sistema de ecuaciones? Evidentemente, resolver el sistema es encontrar los valores (literales o numericos) de las incognitas pero tiene tambien un significado geometrico. En lo que nos importa para la PSU bastenos saber que resolver un sistema de 2x2 es encontrar las coordenadas de interseccion de las dos rectas representadas por las 2 ecuaciones, mientras que resolver un sistema de 3x3 es encontrar las coordenadas del punto de interseccion de los tres planos dados por las tres ecuaciones. No asustarse, en general, una ecuacion de 2 variables determina una superficie en el espacio de las 3 variables posibles del problema (si no entiende esto no se preocupe y siga leyendo con atencion). Por las explicacion anteriores el atento lector habra notado que dos rectas no siempre se cortan en un punto pues pueden tambien ser paralelas o coincidir, o que 3 planos no siempre concurren en un punto pues tambien pueden tener una recta comun, o pueden coincidir completamente, o bien ser paralelos. es nos lleva a ver que un sistema no siempre tiene solucion unica, es mas, no siempre tiene solucion. 1.4 Como resolverlos? Existen varios metodos de resolucion, pero para no provocar un colapso nervioso en el lector solo veremos los mas simples; por sustitucion, igualacion y reduccion. Se explicaran con mas detalle en el proximo tema. -------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Feb 14 2006, 03:17 PM Feb 14 2006, 03:17 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
Tema 2. Metodos de Resolucion
2.1 Sustitucion Este es talves el metodo mas "intuitivo" y la primera forma que a muchos se les ocurre para resolver un sistema, lo que no significa que siempre sea la manera mas facil. Consiste en tomar una ecuacion y despejar un incognita y expresarla en funcion de "todo lo demas", es decir, en funcion de las otras incognitas y de los coeficientes como si se tratase de la unica incognita en la ecuacion. Luego, sustituimos en las otras ecuaciones para obtener un sistema de menos ecuaciones y menos incognitas, hasta resolver alguna incognita para sustituir y seguir con el proceso, hasta resolver todas las incognitas. Veamos ejemplos para sistemas de 2x2 y 3x3. Ejemplo 2.1.1 con un sistema 2x2 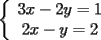 buscando siempre la simpleza, tomaremos la segunda ecuacion y despejaremos 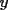 ; ;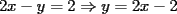 ahora sustituimos el valor de 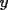 en la primera ecuacion y resolvemos; en la primera ecuacion y resolvemos;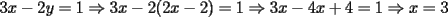 sustituimos 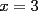 en una de las ecuaciones del sistema, la mas simple naturalmente. En este caso usaremos nuevamente la segunda ecuacion del sistema; en una de las ecuaciones del sistema, la mas simple naturalmente. En este caso usaremos nuevamente la segunda ecuacion del sistema;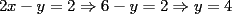 Que el par 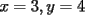 satisface ambas ecuaciones queda como ejercicio para el lector. satisface ambas ecuaciones queda como ejercicio para el lector.Ejemplo 2.1.2 con un sistema de 3x3 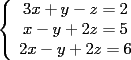 despejamos 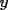 en la primera ecuacion y obtenemos en la primera ecuacion y obtenemos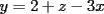 sustituimos 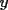 en la segunda ecuacion y obtenemos en la segunda ecuacion y obtenemos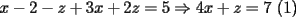 sustituimos 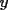 en la tercera ecuacion y obtenemos en la tercera ecuacion y obtenemos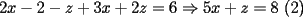 considerando (1) y (2) obtenemos un sistema de 2x2 (que se supone, ya sabemos resolver por sustitucion) 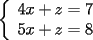 despejamos  en la primera obteniendo en la primera obteniendo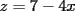 sustituimos en la segunda obteniendo 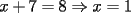 sustituimos 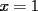 en (1) o (2) y obtenemos en (1) o (2) y obtenemos 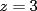 . Con los valores . Con los valores 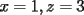 podemos sustituir en una de las 3 ecuaciones originales para obtener el valor de podemos sustituir en una de las 3 ecuaciones originales para obtener el valor de 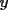 , y facilmente se comprueba en cualquiera de estas 3 ecuacones que , y facilmente se comprueba en cualquiera de estas 3 ecuacones que 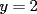 . . Solucion: 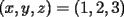
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Feb 16 2006, 05:05 PM Feb 16 2006, 05:05 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
2.2 Igualacion
Consiste en tomar dos ecuaciones y en ambas despejar una variable, digamos en el primer miembro, para luego igualar los segundos miembros de cada ecuacion. Esto se repite hasta llegar a una ecuacion de una sola incognita, para resolverla y sustituir en alguna ecuacion, o respetir todo el proceso para despejar esta vez otra incognita. Recordar que no podemos "inventar" informacion, por ejmplo, si en un sistema de 3x3 con soluciones unicas usamos solo dos de las tres ecuaciones, podemos sospechar que algo anda mal si resolvemos las 3 incognitas. Ejemplo 2.2.1 con un sistema 2x2 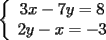 despejemos en ambas  . Llegamos al sistema equivalente . Llegamos al sistema equivalente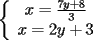 Notar que 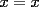 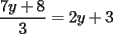 donde resolviendo obtenemos donde resolviendo obtenemos 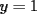 . . Ahora podriamos hacer algo similar a lo anterior, esta vez igualando 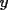 par obtener par obtener  . Pero nos queda mas comodo (y mas rapido) sustituir el . Pero nos queda mas comodo (y mas rapido) sustituir el 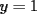 en en 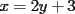 , obteniendo , obteniendo 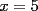 . .Solucion: 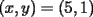 Ejemplo 2.2.2 sistema 3x3 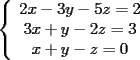 De la primera y la ultima ecuacion obtenemos 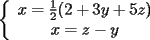 igualamos, operamos y obtenemos 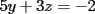 mientras que de la segunda y la ultima ecuacion del sistema obtenemos (despejando la misma incognita que antes): 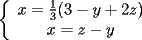 igualamos y llegamos a 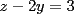 . Por lo anterior se tiene . Por lo anterior se tiene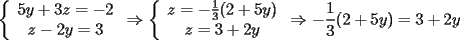 resolviendo obtenemos 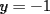 . .Sustituimos en alguna de las ecuaciones del sistema 2x2 anterior (la mas facil). Usemos 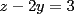 , obtenemos , obtenemos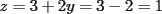 . .Con 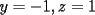 sustituimos en alguna de las ecuaciones del sistema 3x3 original. sustituimos en alguna de las ecuaciones del sistema 3x3 original.Tomemos por ejemplo  , luego , luego 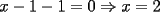 Solucion: 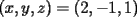
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Feb 17 2006, 02:10 PM Feb 17 2006, 02:10 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
2.3 Reduccion
Tomamos dos o mas ecuaciones del sistema y las amplificamos por algun factor conveniente (entero, fraccionario, positivo, negativo... pero nunca cero) de modo que al sumar estas igualdades miembro a miembro se elimine alguna incognita, o mejor aun, resulte una ecuacion de primer grado con una sola incognita que se supone, a estas alturas ya sabemos resolver (se supone). Ejemplo 2.3.1 con un sistema 2x2 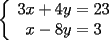 Amplificamos la segunda ecuacion por 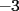 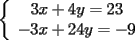 Sumamos miembro a miembro obteniendo 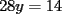 Resolvemos y llegamos a que 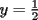 Sustituyendo este valor en la segunda ecuacion del sistema original se tiene 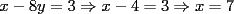 Solucion: 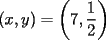 Ejemplo 2.3.2 con un sistema 3x3 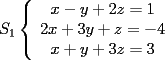 Reducimos la primera con la segunda amplifacando la primera por 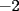 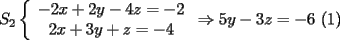 Reducimos la primera con la tercera de 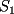 amplificando la primera por amplificando la primera por 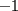 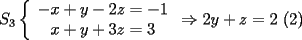 De (1) y (2) se deduce el sistema 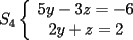 Reducimos este sistema amplificando la segunda por  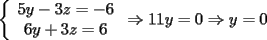 Sustituimos este valor en la segunda ecuacion de 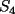 (unico motivo; porque es mas sencillo) y obtenemos (unico motivo; porque es mas sencillo) y obtenemos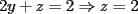 Ahora sustituimos los valores de 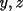 en la tercera de en la tercera de 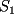 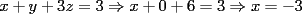 Solucion: 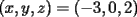
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Feb 21 2006, 01:19 PM Feb 21 2006, 01:19 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 765 Registrado: 6-December 05 Miembro Nº: 458 Nacionalidad:  Sexo:  |
3. Cantidad de Soluciones
Como el objetivo de esta guia es preparacion de PSU, nos centraremos en los sistemas de 2x2 3.1 Solucion Unica Este es el caso mas comun, y del cual nos hemos preocupado hasta ahora. Ocurre cuando un unico par 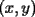 satisface las 2 ecuaciones simultaneamente. satisface las 2 ecuaciones simultaneamente. Significado geometrico: Como ya hemos dicho, las graficas en un plano cartesiano de ambas ecuaciones de un sistema 2x2 corresponden a rectas. Cuando un sistema tiene solucion unica, las rectas se cortan y el unico par 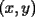 que las satisface corresponde a las coordenadas del punto de interseccion. que las satisface corresponde a las coordenadas del punto de interseccion.Ejemplo 3.1.1 un sistema 2x2 con solucion unica 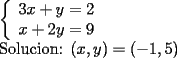 Ejemplo 3.1.2 identificar si un sistema 2x2 tiene solucion unica, sin resolver Verifiquemos si el sistema anterior tiene solucion unica o no. Podriamos resolverlo, pero la idea es siempre ir rapido para ganar tiempo en la PSU, asi que veremos otra manera de saberlo. Si el sistema tiene solucion unica, entonces las graficas de sus ecuaciones son rectas que se cortan, por lo tanto las pendientes de estas rectas son distintas. En el ejemplo; La pendiente de 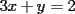 ; ;Expresamos la ecuacion en la forma 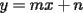 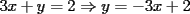 luego, la pendiente de esta ecuacion es 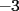 La pendiente de 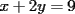 ; ;Expresamos la ecuacion en la forma 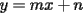 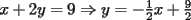 luego, la pendiente de esta ecuacion es 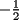 Como las pendientes son distintas, las rectas se cortan y el sistema tiene solo una solucion. 3.1 Ninguna Solucion Ocurre cuando no existe par ordenado alguno de la forma 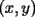 que satisfaga ambas ecuaciones del sistema 2x2 de forma simultanea. que satisfaga ambas ecuaciones del sistema 2x2 de forma simultanea.Significado geometrico: Las rectas dadas por las ecuaciones son paralelas, y por lo tanto, no se cortan. Ejemplo 3.1.1 un sistema 2x2 sin solucion 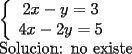 Ejemplo 3.1.2 identificar si un sistema 2x2 no tiene solucion, sin intentar resolverlo como geometricamente se trata de rectas paralelas, tienen igual pendiente pero distinto coeficiente de posicion. Esto es, al expresar las ecuaciones en la forma 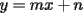 sus valores de sus valores de 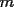 coinciden pero sus valores de coinciden pero sus valores de  son distintos. son distintos.Para el sistema del ejemplo anterior: 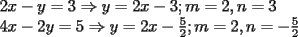 Comprobando facilmente lo explicado. 3.1 Infinitas Soluciones Ocurre cuando existen infinitos pares ordenados 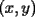 que satisfacen las ecuaciones simultaneamente (notar que "infinitos pares ordenados" no significa que cualquier par ordenado sea solucion). que satisfacen las ecuaciones simultaneamente (notar que "infinitos pares ordenados" no significa que cualquier par ordenado sea solucion).Significado geometrico: Las graficas de ambas ecuaciones corresponden a la misma recta. Otra forma de verlo es decir que las rectas coinciden. Ejemplo 3.1.1 un sistema 2x2 con infinitas soluciones 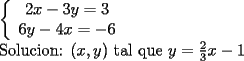 Ejemplo 3.1.2 identificar si un sistema 2x2 infinitas soluciones, sin resolverlo Como geometricamente se trata de la misma recta (o de otra forma, las graficas coinciden) al expresar ambas ecuaciones en la forma 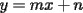 deben coincidir tanto las pendientes como los cieficientes de posicion ( deben coincidir tanto las pendientes como los cieficientes de posicion (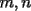 respectivamente). respectivamente).Para el sistema del ejemplo 3.1.1 tenemos: 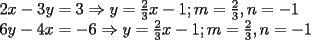 Luego, las rectas coinciden y la unica condicion que deben cumplir 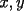 es verificar la ecuacion es verificar la ecuacion 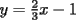 para la cual sabemos que existen infinitas soluciones en los reales. para la cual sabemos que existen infinitas soluciones en los reales.
-------------------- Pasten, un buen muchacho en quien confiar.
|
|
|
|
 Jul 7 2006, 07:59 PM Jul 7 2006, 07:59 PM
Publicado:
#6
|
|
 Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 23 Registrado: 10-April 06 Desde: En kualkier parte Miembro Nº: 816 |
muy buen material...
gracias.. lo estoi leyendo.... y aprendiendo... hacique despues a practicar.... habian cosas que se me habian olvidado pero ahora se me esta refrescando la memoria... saludos -------------------- SI A LAS FINALES
TODOS SOMOS CRESPOS O NO? |
|
|
|
 Jan 10 2007, 10:01 PM Jan 10 2007, 10:01 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Esto es genial...
Muy buen material...( Se agradece... Mensaje modificado por Felipe_ambuli el Feb 19 2007, 07:00 PM |
|
|
|
 Jan 19 2007, 06:28 PM Jan 19 2007, 06:28 PM
Publicado:
#8
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 80 Registrado: 6-June 06 Desde: Argentina Miembro Nº: 1.263 Nacionalidad:  Sexo:  |
Imprecionante!!! queda clarisisisisisimo!!
GRACIAS por el grandioso aporte --------------------  |
|
|
|
 Feb 5 2007, 11:15 AM Feb 5 2007, 11:15 AM
Publicado:
#9
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 166 Registrado: 15-October 06 Desde: desde mi compu en temuco Miembro Nº: 2.532 Nacionalidad:  Universidad:  Sexo:  |
 yo lo quiero dejar pa quien lo quiera bajar pos y asi mostrarselos a sus compañeros por que es muy buen material
Archivo(s) Adjunto(s)
--------------------  weno El hombre que en los mas hondo de su ser, duda de sí mismo, jamás encontrará quien lo acompañe [H. Keyserling.] Allí donde se hicieorn los caminos, o he perdido el mio.(XxryurickxX) Defiende tu derecho a pensar, porque incluso pensar en forma errónea es mejor que no pensar (Hipatia) Si buscas resultados distintos, no hagas siempre lo mismo (Albert Einstein) |
|
|
|
 Feb 5 2007, 11:55 AM Feb 5 2007, 11:55 AM
Publicado:
#10
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Tu idea puede potenciarse aún más.
Solamente copia todo lo que es contenido, y lo matemático lo tipeas tú ya que al pasar en PDF lo copiado, la calidad se pierde y se torna no muy agradable (ahí ves qué procesador de textos matemáticos te gusta más). Una vez hecho eso, me das el archivo y lo paso a un PDF para que la versión del contenido quede imprimible. Saludos |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:47 PM |










