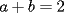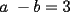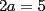|
|
|
|
|
|
|
  |
 Feb 7 2006, 11:37 PM Feb 7 2006, 11:37 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Las potencias es un contenido básico para la PSU, y es un tema importante en la enseñanza media, además de ser una materia simple.
Es necesario tener muy en cuenta esta materia para la PSU, ya que es un tema sencillo, pero que puede tener algunas trampas y puede llegar ser fácil equivocarse en problemas que su solución parecia "obvia". Espero que esta guía les sirva a todos los que dan la PSU este año o los que la daran pronto, y más que desearles suerte... a estudiar Potencias Consideremos 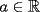 y y 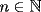 Definiremos como 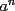 como: como: 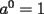 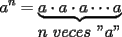 Lo que llamaremos “  elevado a su enésima potencia” donde elevado a su enésima potencia” donde  es la base y es la base y  el exponente. el exponente.Ejemplos: 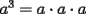 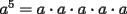 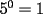 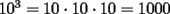 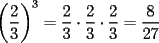 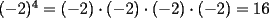 Extenderemos ahora esta definición para 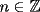 . En particular nos preocuparemos cuando . En particular nos preocuparemos cuando 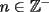 (exponente negativo) donde la definición anterior simplemente no tiene sentido pues no podríamos pensar que: (exponente negativo) donde la definición anterior simplemente no tiene sentido pues no podríamos pensar que: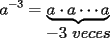 que simplemente sería algo "absurdo". que simplemente sería algo "absurdo".Para este caso la definición acertada será 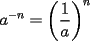 Ejemplos: 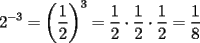 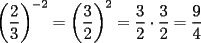 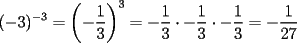 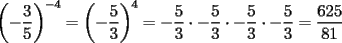
--------------------  |
|
|
|
 Feb 7 2006, 11:39 PM Feb 7 2006, 11:39 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Propiedades de Las Potencias
1) 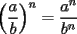 , , 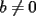 2) 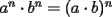 3) 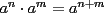 4) 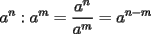 , , 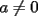 5) 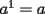 6) 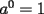 , , 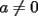 7) 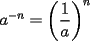 , , 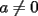 8) 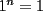 9) ![TEX: $[(a)^n]^m=a^{n \cdot m}$](./tex/29075.gif) 10)  10.1) Si 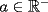 y n par, entonces y n par, entonces 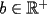 Ejemplo: 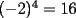 10.2) Si 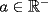 y n impar, entonces y n impar, entonces 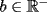 Ejemplo: 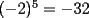 Nota: Como se podrán a ver dado cuenta, varias de estas propiedades tienen restricciones sobre ciertos valores que puede tomar alguna variable, en estos casos todas las restricciones son para evitar la división por 0, ya que ésta no está definida en matemática. --------------------  |
|
|
|
 Feb 7 2006, 11:54 PM Feb 7 2006, 11:54 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problemas Resueltos
Problema 1 Dar ejemplos con números simples todas las propiedades anteriormente nombradas. Solución: Propiedad 1 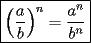 , , 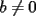 Ejemplo: 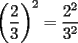 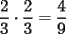 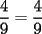 Propiedad 2 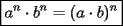 Ejemplo: 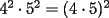 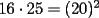 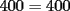 Propiedad 3  Ejemplo: 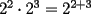 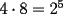 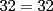 Propiedad 4 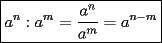 , , 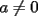 Ejemplo: 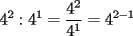 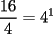 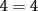 Propiedad 5  Ejemplo: 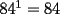 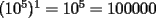 Propiedad 6 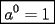 , , 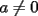 Ejemplo: 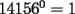 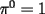 Propuesto: Después de estudiar todas las propiedades presentes en esta guía, demostrar esta propiedad. Propiedad 7 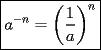 Ejemplo: 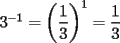 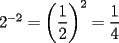 Propiedad 8 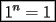 Ejemplo: 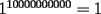 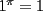 Propiedad 9 ![TEX: $\boxed{[(a)^n]^m=a^{n \cdot m}}$](./tex/29145.gif) Ejemplo: ![TEX: $[(2)^3]^2=2^{3 \cdot 2}$](./tex/29124.gif) 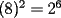 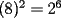 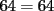
--------------------  |
|
|
|
 Feb 8 2006, 12:18 AM Feb 8 2006, 12:18 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2
El valor de 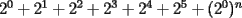 es igual a: es igual a:A) 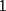 B) 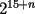 C) 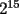 D) 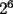 E) Otro Valor Test de Matemática PAA - PCE , Carlos Mercado Shüler Solución: --------------------  |
|
|
|
 Feb 8 2006, 12:20 AM Feb 8 2006, 12:20 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 3
Con respecto a la potenciación se afirma siempre que: I) Es una operación conmutativa 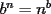 II) Es una operación asocitiva 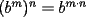 III) Es distributiva con respecto a la multiplicación 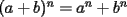 A) Verdadera sólo la I B) Verdadera sólo la II C) Verdadera sólo la III D) Las 3 son verdaderas E) Las 3 son falsas Test de Matemática PAA-PCE, Carlos Mercado Schüler Solución: --------------------  |
|
|
|
 Feb 8 2006, 12:21 AM Feb 8 2006, 12:21 AM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 4
El valor de 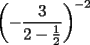 es: es:A) 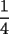 B) 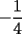 C) 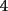 D) 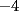 E) Otro Valor Test de Matemática PAA-PCE, Carlos Mercado Schüler Solución: --------------------  |
|
|
|
 Feb 8 2006, 12:23 AM Feb 8 2006, 12:23 AM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 5
El valor de 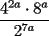 es: es:A)  B) 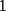 C)  D) 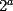 E) 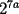 Control Coef. 2 - 2º Medio - E. Guzmán - Instituto Nacional Solución: --------------------  |
|
|
|
 Feb 8 2006, 01:31 AM Feb 8 2006, 01:31 AM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 6
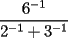 es igual a: es igual a:A) 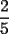 B) 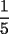 C) 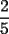 D)  E) 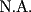 Ensayo PSU 2005 - Instituto Nacional Solución: --------------------  |
|
|
|
 Feb 8 2006, 01:38 AM Feb 8 2006, 01:38 AM
Publicado:
#9
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 7
Si 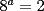 , entonces , entonces 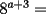 ? ?A) 24 B) 32 C) 48 D) 512 E) 1024 Control Coef 1 - 2º Medio - S. Santaelices - Instituto Nacional Solución: --------------------  |
|
|
|
 Feb 8 2006, 02:17 AM Feb 8 2006, 02:17 AM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Moderador Mensajes: 957 Registrado: 5-November 05 Miembro Nº: 360 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 8
Si 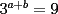 y y 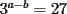 , entonces , entonces 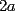 es un´número: es un´número:A) Entero Par B) Entero Impar C) Racional Negativo D) Irracional Positivo E) Irracional Negativo Control Coef. 2 - 2º Medio - E. Guzmán - Instituto Nacional Solución: --------------------  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 09:17 PM |









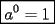 y apliquemosla:
y apliquemosla: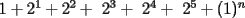
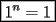
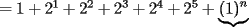
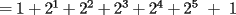

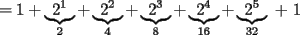
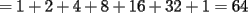
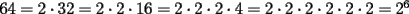
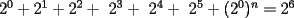
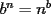 ??
??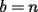 y
y 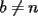 .
.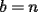 con
con 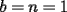
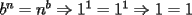
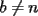 ?
?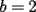 y
y 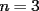
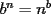
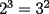
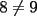
![TEX: $\boxed{[(a)^n]^m=a^{n \cdot m}}$](./tex/29656.gif)
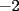 , donde
, donde 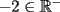 lo que significa que podemos usar la propiedad 7
lo que significa que podemos usar la propiedad 7 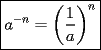
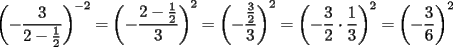
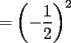
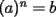 ,
, 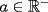 y n par, entonces
y n par, entonces 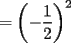
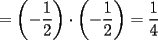
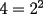
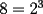
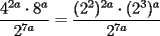
![TEX: $\boxed{[(a)^n]^m=a^{n \cdot m}}$](./tex/31292.gif)
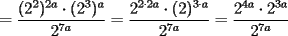
 , entonces:
, entonces: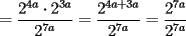
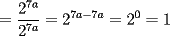
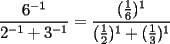
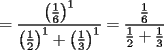
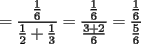
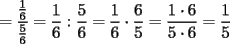

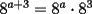
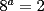 , reemplazamos:
, reemplazamos: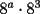
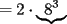
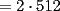
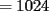
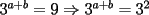
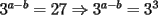
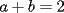
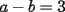
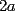 sumamos las 2 ecuaciones:
sumamos las 2 ecuaciones: