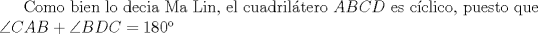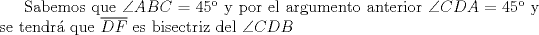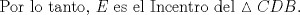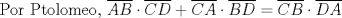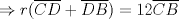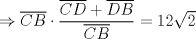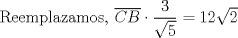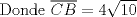|
|
|
|
|
|
|
  |
 Mar 21 2008, 06:01 PM Mar 21 2008, 06:01 PM
Publicado:
#1
|
|
 Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad:  Universidad:  Sexo:  |
--------------------  |
|
|
|
 Mar 11 2010, 04:53 PM Mar 11 2010, 04:53 PM
Publicado:
#2
|
|
 Dios Matemático Grupo: Team Ensayos FMAT Mensajes: 309 Registrado: 2-December 08 Desde: Cerro Navia Miembro Nº: 40.183 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Veamos que tal...
En la figura adjunta se tiene una circunferencia con centro en A y de radio  . .Sea: 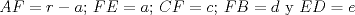 Utilizando las cuerdas 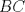 y y 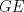 en el teorema de las cuedas, se obtiene: en el teorema de las cuedas, se obtiene: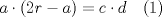 Claramente el cuadrilátero 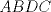 es cíclico, por lo cual es cíclico, por lo cual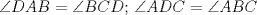 . .Luego se puede deducir que los triángulos 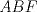 y y 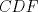 son semejantes, entonces son semejantes, entonces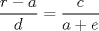 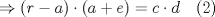 Luego se igualan el primer miembro de la ecuación (1) y (2), 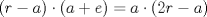 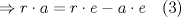 Además se tienen los siguientes datos (mencionados en el enunciado): 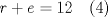 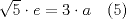 Luego podemos formar un sistema de 3 ecuaciones [(3), (4) y (5)] con tres incógnitas (r, a y e). Al despejar el valor de  , se llega a la siguiente ecuación de 2do grado: , se llega a la siguiente ecuación de 2do grado: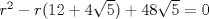 Resolviendo la ecuación se obtienen dos valores para  : 12 y : 12 y 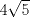 . Claramente el valor de . Claramente el valor de  no puede ser 12, ya que no puede ser 12, ya que  es distinto de cero. es distinto de cero. Por lo tanto, 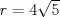 Para finalizar aplicamos el teorema de pitágoras en el triángulo 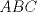 , y obtenemos: , y obtenemos: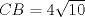 Alternativa C Saludos!!!!  dibujo.JPG ( 11.46k )
Número de descargas: 9
dibujo.JPG ( 11.46k )
Número de descargas: 9 |
|
|
|
 Mar 11 2010, 06:32 PM Mar 11 2010, 06:32 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Colaborador Platinum Mensajes: 1.032 Registrado: 25-March 09 Desde: Quinta Normal Miembro Nº: 46.018 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Tu Solución es correcta y muy bien redactada por lo demás
Además, ocupas sólo PSU, no así mi posible solución: En fin, el problema se dá por resuelto después de casi 2 años, mis felicitaciones Ma Lin |
|
|
|
 Mar 11 2010, 07:59 PM Mar 11 2010, 07:59 PM
Publicado:
#4
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Yo no veo claramente que ABCD sea cíclico
-------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Mar 11 2010, 08:02 PM Mar 11 2010, 08:02 PM
Publicado:
#5
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Huh? Por qué no? Yo lo veo cíclico.
|
|
|
|
 Mar 12 2010, 12:30 PM Mar 12 2010, 12:30 PM
Publicado:
#6
|
|
 Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Huh? Por qué no? Yo lo veo cíclico. Yo también sé que es cíclico, pero una pequeña demostración por parte de Ma Lin no sería malo (de todos modos la demostración sale en una línea xD, pero tal vez para los que se inician no sea tan evidente) -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico  “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti ![TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />](/tex-image/662cf378c88b8d7170f7919ce7dc427a.png) |
|
|
|
 Mar 12 2010, 12:34 PM Mar 12 2010, 12:34 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
|
|
|
|
 Mar 12 2010, 12:55 PM Mar 12 2010, 12:55 PM
Publicado:
#8
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
lo que pasa es que los criterios de ciclicidad, si bien son sencillos y evidentes como dicen ahi, no son tan visitados por el comun de la gente y por tanto no saben bien donde mirar; a este punto es donde se considera "no evidente".
para quien se complique aun la existencia con dicha afirmacion note simplemente que el cuadrilatero tiene dos angulos opuestos suplementarios. ¿Costaba tanto decir eso? -------------------- |
|
|
|
 Mar 12 2010, 01:05 PM Mar 12 2010, 01:05 PM
Publicado:
#9
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
De hecho ni siquiera costaba decirlo, pues está en la segunda línea de la solución de Tela.
|
|
|
|
 Apr 29 2010, 12:15 PM Apr 29 2010, 12:15 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 19th April 2025 - 08:28 AM |





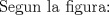
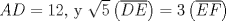
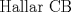

![TEX: \[<br />\begin{gathered}<br /> a)2\sqrt {10} \hfill \\<br /> b)2\sqrt 5 \hfill \\<br /> c)4\sqrt {10} \hfill \\<br /> d)4\sqrt 5 \hfill \\<br /> e)3\sqrt {10} \hfill \\ <br />\end{gathered} <br />\]](./tex/c4cb87d5cd24baf2a182109aa735d8d2.png)