|
|
|
|
|
|
|
  |
 Feb 7 2006, 12:11 AM Feb 7 2006, 12:11 AM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
Pre- Data:Lo que está encerrado en un rectángulo son las fórmulas finales!!.
Este temita es más que recurrente en la PSU y en todo lo que involucre Álgebra. Es un tema que todos, sin excepción alguna debe manejar para rendir esta prueba. Es por esto que se me ha encargado poner a vuestra disposición una guía explicando de la mejor manera posible todo lo referido a este tema. Haré lo mejor que pueda!! A mi entender, una buena forma de comenzar a familiarizarce con las factorizaciones básicas, es partiendo por los Productos notables: PRODUCTOS NOTABLES Los "Productos Notables" son multiplicaciones de expresiones algebráicas cuyo resultado puede aprenderse de memoria sin realizar la multiplicación término a término! Es como un equivalente a las tablas de multiplicar en el álgebra elemental. Las Principales que DEBES manejar para la PSU son: 1) Cuadrado de Binomio 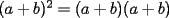 / Multiplicando término a término / Multiplicando término a término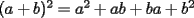 / Agrupando Términos Semejantes / Agrupando Términos Semejantes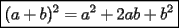 / Fórmula del Cuadrado de la suma de dos cantidades! / Fórmula del Cuadrado de la suma de dos cantidades!Propuesto: Verificar utilizando la multiplicación término a término que: 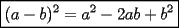 2) Suma por su Diferencia 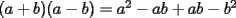 / Notemos que ab-ab se aniquilan. / Notemos que ab-ab se aniquilan.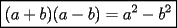 / Para el que no se ha dado cuenta esta es más repetida que el chavo del ocho. / Para el que no se ha dado cuenta esta es más repetida que el chavo del ocho.3) Cubo de Binomio 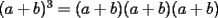 / Notemos que es lo mismo que / Notemos que es lo mismo que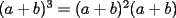 / Que, como vimos antes, se puede escribir / Que, como vimos antes, se puede escribir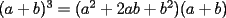 / Multiplicando término a término / Multiplicando término a término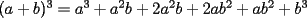 / Agrupando / Agrupando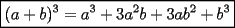 Propuesto: Verificar utilizando el proceso anterior: 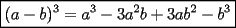 4) Producto de Binomios con un término en Común ( 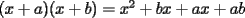 / de ( / de ( 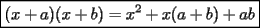 5) Producto que da suma de cubos perfectos  / Luego / Luego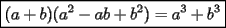 6) Producto que da diferencia de cubos perfectos 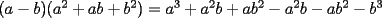 / Luego / Luego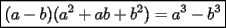 Esos son! RESUMIENDO: 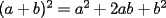 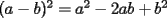 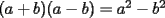 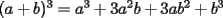 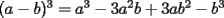 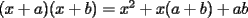 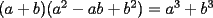 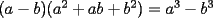 Nota Importante : La gracia de esto es que si se te olvida alguna fórmula, siempre puedes deducirla tal y como se hizo con cada una anteriormente. -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 7 2006, 12:15 AM Feb 7 2006, 12:15 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
FACTORIZACIONES
Bueno, como lo prometido es deuda, aqui vamos con la sección de Factorizaciones básicas. Está de más decir que no puedes prescindir de estos conocimientos si tu objetivo es rendir aceptablemente la PSU de matemáticas. Nos basaremos bastante en ejemplos. Es necesario entender y, en lo posible, saberse las fórmulas de los productos notables. Si aún no te las aprendes de memoria, no te preocupes... con todos los ejercicios que vas a hacer luego de leer esta guia te los aprenderás de memoria. Here we go: ¿QUÉ ES FACTORIZAR? Factorizar, como su nombre nos lo indica, es expresar un polinomio o una exprresión algebráica cualquiera como el producto de sus factores. Nuestra tarea será descubrir estos factores. Ejemplo Ubiquemos los factores de 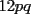 : :Claramente son 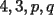 , puesto que: , puesto que: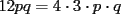 Ahora si vamos con nuestros casos: 1) FACTOR COMÚN: MONOMIO Nos encontramos con este caso cuando en un polinomio todos los sumandos tienen un mismo factor en común. Una vez que hayamos descubierto este factor común, procedemos a factorizar. Ejemplo Intentemos Factorizar la expresión 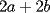 - Nos damos cuenta que el factor común es  . Lo escribiremos fuera del paréntesis. . Lo escribiremos fuera del paréntesis.- Escribiremos en el otro factor, dentro del paréntesis, los cuocientes entre cada sumando y el factor común. Luego: 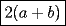 Básicamente, esos son los pasos a seguir. Simple y rápido. 2) FACTOR COMÚN: POLINOMIO La única diferencia con el caso anterior, es que el factor común es un polinomio (entre nos, generalmente un binomio): [bEjemplo[/b] Intentemos Factorizar la expresión 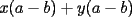 Debemos seguir LA MISMA REGLA que utilizamos anteriormente, sólo debemos notar que en este caso, el factor en común corresponde a un nunca bien ponderado Binomio. Luego: 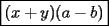 - Dejamos de fuera de nuestro paréntesis el factor común  - Anotamos la suma cuocientes dentro. Hemos seguido la misma idea del caso anterior. Viendo los ejercicios resueltos verán que no hay nada más que explicar. 3) FACTOR COMÚN POR AGRUPACIÓN DE TÉRMINOS La mejor forma de explicarlo es vía ejemplos: Ejemplo Intentemos Factorizar la expresión 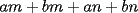 Nuestro método consiste en agrupar los términos que vemos que tienen un factor en común. 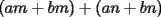 / Notamos que están m y n en común. Apliquemos lo aprendido anteriormente. / Notamos que están m y n en común. Apliquemos lo aprendido anteriormente.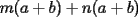 / Aplicando nuestro 2º caso. / Aplicando nuestro 2º caso.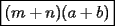 Podemos notar que la única "dificultad" en este caso fue saber agrupar los términos de manera correcta. Propuesto: Llegue al mismo resultado utilizando otra agrupación de términos. 4) TRINOMIO CUADRADO PERFECTO A partir de este caso, podremos notar que corresponden a los mismos que vimos en los PRODUCTOS NOTABLES. (Obviamente debes leerlos al revés, jeje). Diremos que una cantidad es cuadrado perfecto, cuando es el producto de dos cantidades iguales. Por ejemplo, 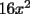 es cuadrado perfecto, puesto que es el cuadrado de es cuadrado perfecto, puesto que es el cuadrado de 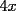 . .Definición: Diremos que un trinomio es cuadrado perfecto, cuando es el cuadrado de un binomio.. Ejemplo Factorizar 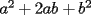 Si un trinomio tiene la forma anterior, como ya vimos en Productos notables, se puede escribir: 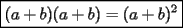 Como podrás darte cuenta, debes fijarte en lo siguiente: - Dos de los términos del trinomio son cuadrados perfectos - El otro término, es (más o menos) el doble del producto de las raíces entre los otros dos. El signo de este término determinará el signo con el que escribamos el binomio. Si el trinomio cumple estas condiciones, es un cuadrado perfecto. 5) DIFERENCIA DE CUADRADOS Te sonará conocido. Claro, puesto que ya lo vimos en Productos Notables. Definición: Cuando nos encontramos con una diferencia de cuadrados perfectos, esta puede escribirse como el producto entre, la suma de las raices de sus términos y la diferencia entre sus raíces. Ejemplo 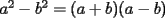 / ¡Tal y como vimos anteriormente, solo que al revés!... (Obvio microbio... estamos haciendo el proceso inverso). / ¡Tal y como vimos anteriormente, solo que al revés!... (Obvio microbio... estamos haciendo el proceso inverso).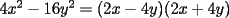 Ojo: Este es seguramente el caso más recurrente. 6) TRINOMIO DE LA FORMA 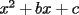 Diremos que un trinomio tiene esta forma cuando: - El coeficiente numérico del primer término es 1. - El factor literal en el primer término está elevado al cuadrado. - El factor literal se encuentra tambien en el segundo término, pero no elevado al cuadrado. - El coeficiente del segundo término puede ser un numero cualesquiera. - El último término es independiente de la letra anterior y puede ser cualquier número. Así, el trinomio tiene la forma 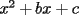 ¿Cómo lo factorizamos? Para factorizar un trinomio de esta forma, debemos seguir los siguientes pasos: - Escribir como dos factores, cada uno entre paréntesis. En cada paréntesis escribir el factor literal correspondiente al trinomio. - Sumando o restándose al factor literal, debemos colocar (uno en cada paréntesis), dos numeros, tales que:Sumados, equivalgan al término 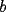 , y su producto, sea igual al término , y su producto, sea igual al término  . .Ejemplos 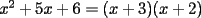 / Note que / Note que 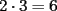 y además y además 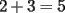 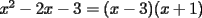 / Puesto que / Puesto que 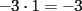 y a su vez, y a su vez, 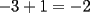 7) TRINOMIO DE LA FORMA 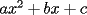 Tiene la misma forma del trinomio anterior, solo que en este caso, el factor  es distinto de es distinto de 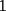 . (Y claramente de . (Y claramente de  ). ).¿Cómo factorizarlo? Es, para mi gusto, el sistema más tedioso. Pero, una vez que se comprende bien, resulta siendo bastante fácil, como todos los demas por cierto Lo haremos mediante un ejemplo: Ejemplo 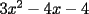 / Multiplicaremos convenientemente por / Multiplicaremos convenientemente por  . (Luego deberemos dividir por 3, para volver a la expresión original). . (Luego deberemos dividir por 3, para volver a la expresión original).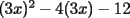 / Voilá!, hemos hecho aparecer nuestro caso anterior!. Luego, buscamos los números que sumados nos den / Voilá!, hemos hecho aparecer nuestro caso anterior!. Luego, buscamos los números que sumados nos den 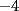 y multiplicados nos den y multiplicados nos den 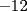 para factorizar para factorizar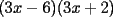 / Ahora debemos dividir por / Ahora debemos dividir por  para volver a la expresión original. para volver a la expresión original.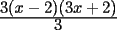 / Factorizamos arriba para poder simplificar, Luego. / Factorizamos arriba para poder simplificar, Luego.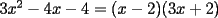 Fácil y Bonito!. Puedes ver más ejemplos resueltos en el post siguiente. Los pasos a seguir son siempre los mismos. Claramente debes aplicar tu ingenio algunas veces. (Aunque ni tanto en la PSU 8) CUBO PERFECTO DE UN BINOMIO Aunque la fórmula se vea un poco fea, basta con estar bien atento para pillar uno de estos. Bueno, no hay mucho que decir al respecto, como ya lo vimos en Productos Notables. Cuando tenemos un polinomio de la forma: 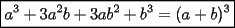 Análogamente: 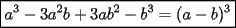 Tiene generalmente la siguiente forma (cambia cuando los términos están desordenados): Primer término al cubo, más (menos) el triple del primero al cuadrado por el segundo, mas el triple del primero por el segundo al cuadrado, mas (menos) el segundo al cubo. 9) SUMA Y DIFERENCIA DE CUBOS Tal y como vimos en productos notables. (Recuerda que este es el PROCESO INVERSO). Atentos, este caso es bastante recurrente. Cuando tenemos una Suma de Cubos: 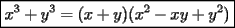 Cuando tenemos una Diferencia de Cubos: 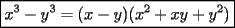 Se pueden escribir de esa forma. ------------------------------------------------------------------------------------------ DATO UTIL: Debes tener muy en cuenta, que para comprobar si la factorización ha sido bien hecha, puedes multiplicar los factores término a término. Si el resultado es el mismo con el que partiste... obviamente lo hiciste bien. -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 7 2006, 12:16 AM Feb 7 2006, 12:16 AM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
Ejercicios Resueltos
Factorizar: 1) 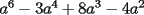 Notamos que el Factor común es 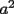 , y aplicando directamente los conocimientos adquiridos: , y aplicando directamente los conocimientos adquiridos: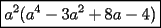 2) 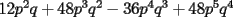 El Factor Común es la mínima expresión que divide a todos los miembros, en este caso 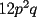 , luego: , luego: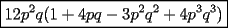 3) 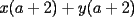 Notemos la existencia de un Factor Común 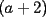 . Luego, factorizando: . Luego, factorizando: 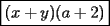 4) 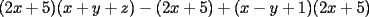 De la misma forma, sólo que esta vez el binomio 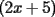 es el factor común: es el factor común: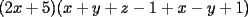 / Agrupando Términos semejantes. / Agrupando Términos semejantes.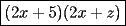 5) 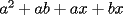 Por Agrupación: 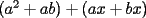 / Factorizando en cada binomio / Factorizando en cada binomio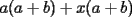 / Factorización final. / Factorización final.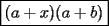 6) 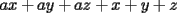 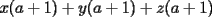 / Luego / Luego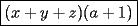 7) 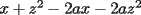 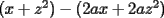 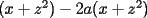 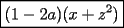 8) 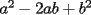 Este es absolutamente directo, es un cuadrado perfecto: 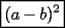 9) 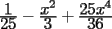 Analizando sólo un poco, podremos notar que se trata de un cuadrado perfecto, luego: 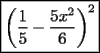 10) 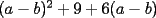 Otro cuadrado perfecto, debes notar que esta vez el primer término es todo un binomio, luego: 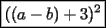 11) 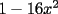 Diferencia de cuadrados directa. Nunca olvides que (como decía mi profe), el 1 es "Comodín", puede expresarse como 1 elevado a cualquier cosa, en este caso, al cuadrado; luego: 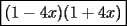 12) 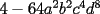 Otra diferencia de cuadrados, sin asustarse: 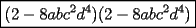 13) 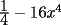 Ya que somos expertos en diferencias de cuadrados, esta es pan comido: 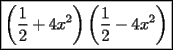 14)  Notemos que: 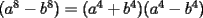 / De igual forma / De igual forma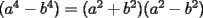 / De nuevo / De nuevo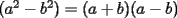 / Luego / Luego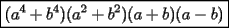 15) 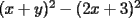 Esta vez son los binomios los que están al cuadrado, lo que no nos hace ni cosquillas: 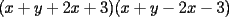 / Términos semejantes / Términos semejantes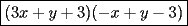 16) 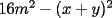 Qué facil, ¿no?: 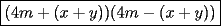 17) 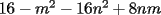 Este hay que observarlo bien. Notemos que ordenando de la siguiente forma todo se aclara: 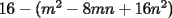 / O lo que es igual [Cuadrado Perfecto] / O lo que es igual [Cuadrado Perfecto]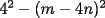 / Finalmente / Finalmente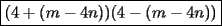 18) 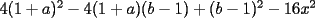 Solo basta notar que los tres primeros términos forman un cuadrado de binomio, y hacer lo mismo que en el ejercicio anterior: 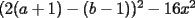 / Luego, diferencia de cuadrados / Luego, diferencia de cuadrados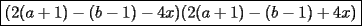 19) 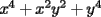 Bueno aqui debemos usar un pequeño truquito, para hacer aparecer una expresión que nos gustaría: 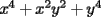 / Le sumamos / Le sumamos  . "Nikita Nipone", verán que sirve mucho. [Notar que lo que hicimos fue "sumar 0"] . "Nikita Nipone", verán que sirve mucho. [Notar que lo que hicimos fue "sumar 0"]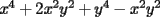 / Eureka! / Eureka!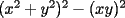 / Luego / Luego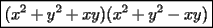 20) 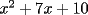 Bueno, como vimos antes, es solo cosa de encontrar dos números que multiplicados den 10 y sumados den 7: 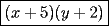 21) 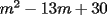 De la misma forma: 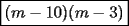 22) 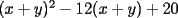 Claramente, este trinomio tiene la forma 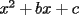 : :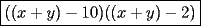 23) 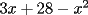 Astutamente, factorizamos por -1: 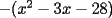 / Luego de esto, es lo mismo / Luego de esto, es lo mismo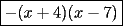 24) 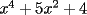 A estas alturas, te resultará facil notarlo: 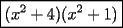 25) 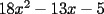 Bueno notamos rápidamente que se trata de un simple trinomio de la forma 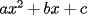 , por lo tanto seguiremos el proceso que aprendimos, partamos multiplicando por 18: , por lo tanto seguiremos el proceso que aprendimos, partamos multiplicando por 18: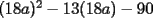 / Factorizando esta expresión / Factorizando esta expresión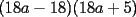 / Ahora debemos dividir por 18 / Ahora debemos dividir por 18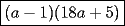 26) 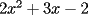 El mismo caso anterior, multipliquemos por 2: 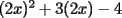 / Factorizando / Factorizando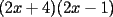 / Dividiendo por 2 / Dividiendo por 2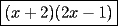 27) 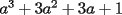 Nos encontramos con un cubo perfecto, que finalmente se escribirá así: 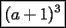 28) 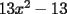 Bueno, este es un caso combinado simple. Primero sacamos factor común: 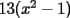 / Además nos encontramos con una Dif. de cuadrados / Además nos encontramos con una Dif. de cuadrados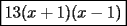 29) 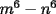 Otro lindo caso combinado que pone a prueba lo que hemos aprendido. Notemos que de partida es una diferencia de cuadrados: 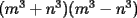 / Una suma y una diferencia de cubos! / Una suma y una diferencia de cubos!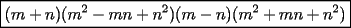 30) 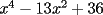 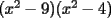 / Ahora factorizando las diferencias de cuadrados / Ahora factorizando las diferencias de cuadrados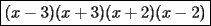 --------------------------------------------------------------------------------------- Bueno, con eso he concluido esta guía. Traté de hacerla lo más completa posible, de forma tal que pueda significar una ayuda real para quienes se estén preparando para la PSU o para quienes simplemente están iniciando en el fascinante mundo del álgebra. Ha sido un gusto. FIN -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 7 2006, 12:35 AM Feb 7 2006, 12:35 AM
Publicado:
#4
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 178 Registrado: 28-May 05 Desde: Aca , alla , aca , alla Miembro Nº: 70 Nacionalidad:  Universidad:  Sexo:  |
Quizas seria bueno que dejaras un espacio entre cada linea con latex de desarrollo , se ve mucho mejor , prueba y ve si te gusta, era solo una sugerencia porq la guia esta buena esta bien completa!!
-------------------- Por un lado la matematica , lo mas importante , pero por el otro el basquetbol y ginobili lo mejor q hay!!!!
Team Naranja!!! Apagando incendios xD    |
|
|
|
 Feb 7 2006, 12:52 AM Feb 7 2006, 12:52 AM
Publicado:
#5
|
|
|
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 194 Registrado: 13-May 05 Desde: jojo! Miembro Nº: 4 Nacionalidad:  Sexo:  |
Muchas gracias cumpa!!!!!!
Esta quedando la **** esta guia |
|
|
|
 Feb 7 2006, 07:19 PM Feb 7 2006, 07:19 PM
Publicado:
#6
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 21-January 06 Desde: Stgo - Chile Miembro Nº: 508 Nacionalidad:  Sexo:  |
la verdad que si. Va quedando super bien! Como ya dije está entendible, bien hecha y ordenada. Felicitaciones ^^ Seguro que cuando la termines va a quedar excelente
--------------------  Nunca pienses en la suerte, porque es el pretexto de los fracasos |
|
|
|
 Feb 17 2006, 02:09 PM Feb 17 2006, 02:09 PM
Publicado:
#7
|
|
 Coordinador Team PreuVirtual Grupo: Usuario FMAT Mensajes: 1.447 Registrado: 2-February 06 Desde: Valparaiso Miembro Nº: 531 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
esta muy bueno, debo aprenderme esto
-------------------- |
|
|
|
 Feb 17 2006, 09:11 PM Feb 17 2006, 09:11 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
MISION CUMPLIDA!!!
Mensaje modificado por Gazoo el Feb 21 2006, 11:36 PM -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 22 2006, 12:33 AM Feb 22 2006, 12:33 AM
Publicado:
#9
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 21-January 06 Desde: Stgo - Chile Miembro Nº: 508 Nacionalidad:  Sexo:  |
no podía dejar de postear el primer post después del ultraesfuerzo (ni tanto, pero parece que fue harto tiempo invertido jajajaja) sin felicitarte. Como dije antes, lo que llevabas al principio se veía genial y ahora que esta terminada y por lo que vi, pues realmente quedó buenísima. Mañana la leo más detenidamente, demás que hay cosas que o no me acuerdo o nunca me aprendi jaajaja
Saludos ^^ --------------------  Nunca pienses en la suerte, porque es el pretexto de los fracasos |
|
|
|
 Feb 22 2006, 11:18 PM Feb 22 2006, 11:18 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
sin palabras... mis más sinceras felicitaciones... -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th April 2025 - 05:00 PM |













