Simpatica - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Desigualdades > Problemas Resueltos

Reply to this topic

Start new topic

Simpatica, Resuelto por Caetano [básico]

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 2 2006, 02:56 AM Publicado: #1
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	Sean 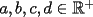$TEX: $a,b,c,d\in\mathbb{R}^+$$ Probar que: $TEX: $\displaystyle\sqrt{\frac{a^2+b^2+c^2+d^2}{4}}\ge\sqrt[3]{\frac{abc+abd+acd+bcd}{4}}$$ Ojo que este es un caso particular de una desigualdad conocida....pero no acepto menciones a desigualdades que no sepan demostrar o cuyas demostraciones no esten en el foro. Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Caetano Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 10 2006, 03:42 AM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 293 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 3 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Notese que demostrar la desigualdad anterior es equivalente a demostrar que: 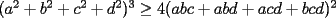$TEX: $(a^2+b^2+c^2+d^2)^3\ge 4(abc+abd+acd+bcd)^2$$ Notemos que: 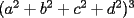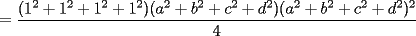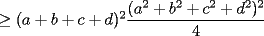$TEX: $(a^2+b^2+c^2+d^2)^3$$ $TEX: $=\displaystyle\frac{(1^2+1^2+1^2+1^2)(a^2+b^2+c^2+d^2)(a^2+b^2+c^2+d^2)^2}{4}$$ $TEX: $\ge (a+b+c+d)^2\displaystyle\frac{(a^2+b^2+c^2+d^2)^2}{4}$$ (Esto ultima por desigualdad de Cauchy-Shwarz) $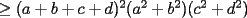TEX: $\ge (a+b+c+d)^2(a^2+b^2)(c^2+d^2)$$ (Esto ultimo por la desigualdad $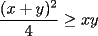TEX: $\displaystyle\frac{(x+y)^2}{4}\ge xy$$ ) $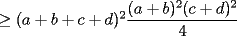TEX: $\ge (a+b+c+d)^2\displaystyle\frac{(a+b)^2(c+d)^2}{4}$$ (Esto ultimo por la desigualdad $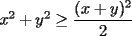TEX: $x^2+y^2\ge \displaystyle\frac{(x+y)^2}{2}$$ ) $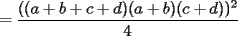TEX: $=\displaystyle\frac{((a+b+c+d)(a+b)(c+d))^2}{4}$$ $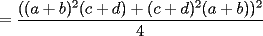TEX: $=\displaystyle\frac{((a+b)^2(c+d)+(c+d)^2(a+b))^2}{4}$$ $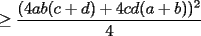TEX: $\ge \displaystyle\frac{(4ab(c+d)+4cd(a+b))^2}{4}$$ (Esto ultimo por la desigualdad $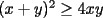TEX: $(x+y)^2\ge 4xy$$ ) $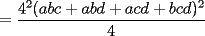TEX: $=\displaystyle\frac{4^2(abc+abd+acd+bcd)^2}{4}$$ $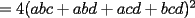TEX: $=4(abc+abd+acd+bcd)^2$$ Concluyendo asi el problema --------------------

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 10 2006, 03:55 AM Publicado: #3
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(Caetano @ Feb 10 2006, 05:42 AM) Notese que demostrar la desigualdad anterior es equivalente a demostrar que: 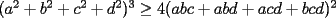$TEX: $(a^2+b^2+c^2+d^2)^3\ge 4(abc+abd+acd+bcd)^2$$ Notemos que: 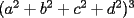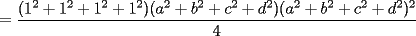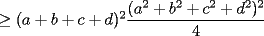$TEX: $(a^2+b^2+c^2+d^2)^3$$ $TEX: $=\displaystyle\frac{(1^2+1^2+1^2+1^2)(a^2+b^2+c^2+d^2)(a^2+b^2+c^2+d^2)^2}{4}$$ $TEX: $\ge (a+b+c+d)^2\displaystyle\frac{(a^2+b^2+c^2+d^2)^2}{4}$$ (Esto ultima por desigualdad de Cauchy-Shwarz) $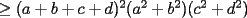TEX: $\ge (a+b+c+d)^2(a^2+b^2)(c^2+d^2)$$ (Esto ultimo por la desigualdad $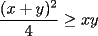TEX: $\displaystyle\frac{(x+y)^2}{4}\ge xy$$ ) $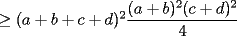TEX: $\ge (a+b+c+d)^2\displaystyle\frac{(a+b)^2(c+d)^2}{4}$$ (Esto ultimo por la desigualdad $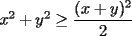TEX: $x^2+y^2\ge \displaystyle\frac{(x+y)^2}{2}$$ ) $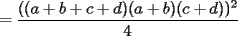TEX: $=\displaystyle\frac{((a+b+c+d)(a+b)(c+d))^2}{4}$$ $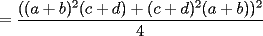TEX: $=\displaystyle\frac{((a+b)^2(c+d)+(c+d)^2(a+b))^2}{4}$$ $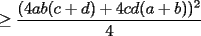TEX: $\ge \displaystyle\frac{(4ab(c+d)+4cd(a+b))^2}{4}$$ (Esto ultimo por la desigualdad $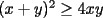TEX: $(x+y)^2\ge 4xy$$ ) $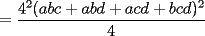TEX: $=\displaystyle\frac{4^2(abc+abd+acd+bcd)^2}{4}$$ $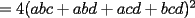TEX: $=4(abc+abd+acd+bcd)^2$$ Concluyendo asi el problema Respuesta correcta y muy bonita... Felicitaciones -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 8th April 2025 - 12:11 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.