Para practicar Chebyshev - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Desigualdades > Problemas Resueltos

Para practicar Chebyshev, no tan fácil... Resuelto por TheLord [básico]

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 10 2007, 01:50 AM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: 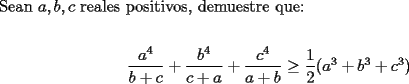Sexo:	$TEX: \noindent Sean $a,b,c$ reales positivos, demuestre que:\\<br />\begin{center}<br />$\dfrac{a^4}{b+c}+\dfrac{b^4}{c+a}+\dfrac{c^4}{a+b}\ge \dfrac{1}{2}(a^3+b^3+c^3)$<br />\end{center}$ Saludos

Start new topic

Respuestas (1 - 6)

iMPuRe Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 11 2007, 09:07 PM Publicado: #2
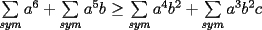Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Lo anterior por expansion, amplificacion por $TEX: $2$$ y cancelacion de terminos es equivalente a $TEX: $\sum\limits_{sym} {a^6}+\sum\limits_{sym} {a^5b} \ge \sum\limits_{sym} {a^4b^2}+\sum\limits_{sym} {a^3b^2c}$$ , y esto ultimo es cierto sumando las desigualdades de Muirhead para los vectores $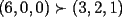TEX: $(6,0,0) \succ (3,2,1)$$ y $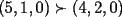TEX: $(5,1,0) \succ (4,2,0)$$ . -------------------- 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311 2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407 3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023 5039 5051 5059 5077 5081 5087 5099 5101 5107 5113 5119 5147 5153 5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279 5281 5297 5303 5309 5323 5333 5347 5351 5381 5387 5393 5399 5407 5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501 5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623 5639 5641 5647 5651 5653 5657 5659 5669 5683 5689 5693 5701 5711 5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827 5839 5843 5849 5851 5857 5861 5867 5869 5879 5881 5897 5903 5923 5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067 6073 6079 6089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173 6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277 6287 6299 6301 6311 6317 6323 6329 6337 6343 6353 6359 6361 6367 6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521 6529 6547 6551 6553 6563 6569 6571 6577 6581 6599 6607 6619 6637 6653 6659 6661 6673 6679 6689 6691 6701 6703 6709 6719 6733 6737 6761 6763 6779 6781 6791 6793 6803 6823 6827 6829 6833 6841 6857 6863 6869 6871 6883 6899 6907 6911 6917 6947 6949 6959 6961 6967 6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069 7079 7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211 7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331 7333 7349 7351 7369 7393 7411 7417 7433 7451 7457 7459 7477 7481 7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7873 7877 7879 7883 7901 7907 7919 7927 7933 7937 7949 7951 7963 7993 8009 8011 8017 8039 8053 8059 8069 8081 8087 8089 8093 8101 8111 8117 8123 8147 8161 8167 8171 8179 8191 8209 8219 8221 8231 8233 8237 8243 8263 8269 8273 8287 8291 8293 8297 8311 8317 8329 8353 8363 8369 8377 8387 8389 8419 8423 8429 8431 8443 8447 8461 8467 8501 8513 8521 8527 8537 8539 8543 8563 8573 8581 8597 8599 8609 8623 8627 8629 8641 8647 8663 8669 8677 8681 8689 8693 8699 8707 8713 8719 8731 8737 8741 8747 8753 8761 8779 8783 8803 8807 8819 8821 8831 8837 8839 8849 8861 8863 8867 8887 8893 8923 8929 8933 8941 8951 8963 8969 8971 8999 9001 9007 9011 9013 9029 9041 9043 9049 9059 9067 9091 9103 9109 9127 9133 9137 9151 9157 9161 9173 9181 9187 9199 9203 9209 9221 9227 9239 9241 9257 9277 9281 9283 9293 9311 9319 9323 9337 9341 9343 9349 9371 9377 9391 9397 9403 9413 9419 9421 9431 9433 9437 9439 9461 9463 9467 9473 9479 9491 9497 9511 9521 9533 9539 9547 9551 9587 9601 9613 9619 9623 9629 9631 9643 9649 9661 9677 9679 9689 9697 9719 9721 9733 9739 9743 9749 9767 9769 9781 9787 9791 9803 9811 9817 9829 9833 9839 9851 9857 9859 9871 9883 9887 9901 9907 9923 9929 9931 9941 9949 9967 9973 10007

Gazoo Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 11 2007, 09:32 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo: Universidad: Sexo:	Creo que hay algun pequeño error de tipeo en el enunciado del problema , pues basta hacer a=0 y b=0 para que no se cumpla... pero imagino que es un detalle de tipeo que se le pasó a Luffy -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein. Estudiante Ingeniería Civil Eléctrica - DIE USACH

iMPuRe Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 11 2007, 09:34 PM Publicado: #4
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 193 Registrado: 22-March 07 Desde: San Miguel, Santiago Miembro Nº: 4.651 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Gazoo @ Sep 11 2007, 10:32 PM) Creo que hay algun pequeño error de tipeo en el enunciado del problema , pues basta hacer a=0 y b=0 para que no se cumpla... pero imagino que es un detalle de tipeo que se le pasó a Luffy igual se entiende creo xd Mensaje modificado por iMPuRe el Sep 11 2007, 09:36 PM -------------------- 2 3 5 7 11 13 17 19 23 29 31 37 41 43 47 53 59 61 67 71 73 79 83 89 97 101 103 107 109 113 127 131 137 139 149 151 157 163 167 173 179 181 191 193 197 199 211 223 227 229 233 239 241 251 257 263 269 271 277 281 283 293 307 311 313 317 331 337 347 349 353 359 367 373 379 383 389 397 401 409 419 421 431 433 439 443 449 457 461 463 467 479 487 491 499 503 509 521 523 541 547 557 563 569 571 577 587 593 599 601 607 613 617 619 631 641 643 647 653 659 661 673 677 683 691 701 709 719 727 733 739 743 751 757 761 769 773 787 797 809 811 821 823 827 829 839 853 857 859 863 877 881 883 887 907 911 919 929 937 941 947 953 967 971 977 983 991 997 1009 1013 1019 1021 1031 1033 1039 1049 1051 1061 1063 1069 1087 1091 1093 1097 1103 1109 1117 1123 1129 1151 1153 1163 1171 1181 1187 1193 1201 1213 1217 1223 1229 1231 1237 1249 1259 1277 1279 1283 1289 1291 1297 1301 1303 1307 1319 1321 1327 1361 1367 1373 1381 1399 1409 1423 1427 1429 1433 1439 1447 1451 1453 1459 1471 1481 1483 1487 1489 1493 1499 1511 1523 1531 1543 1549 1553 1559 1567 1571 1579 1583 1597 1601 1607 1609 1613 1619 1621 1627 1637 1657 1663 1667 1669 1693 1697 1699 1709 1721 1723 1733 1741 1747 1753 1759 1777 1783 1787 1789 1801 1811 1823 1831 1847 1861 1867 1871 1873 1877 1879 1889 1901 1907 1913 1931 1933 1949 1951 1973 1979 1987 1993 1997 1999 2003 2011 2017 2027 2029 2039 2053 2063 2069 2081 2083 2087 2089 2099 2111 2113 2129 2131 2137 2141 2143 2153 2161 2179 2203 2207 2213 2221 2237 2239 2243 2251 2267 2269 2273 2281 2287 2293 2297 2309 2311 2333 2339 2341 2347 2351 2357 2371 2377 2381 2383 2389 2393 2399 2411 2417 2423 2437 2441 2447 2459 2467 2473 2477 2503 2521 2531 2539 2543 2549 2551 2557 2579 2591 2593 2609 2617 2621 2633 2647 2657 2659 2663 2671 2677 2683 2687 2689 2693 2699 2707 2711 2713 2719 2729 2731 2741 2749 2753 2767 2777 2789 2791 2797 2801 2803 2819 2833 2837 2843 2851 2857 2861 2879 2887 2897 2903 2909 2917 2927 2939 2953 2957 2963 2969 2971 2999 3001 3011 3019 3023 3037 3041 3049 3061 3067 3079 3083 3089 3109 3119 3121 3137 3163 3167 3169 3181 3187 3191 3203 3209 3217 3221 3229 3251 3253 3257 3259 3271 3299 3301 3307 3313 3319 3323 3329 3331 3343 3347 3359 3361 3371 3373 3389 3391 3407 3413 3433 3449 3457 3461 3463 3467 3469 3491 3499 3511 3517 3527 3529 3533 3539 3541 3547 3557 3559 3571 3581 3583 3593 3607 3613 3617 3623 3631 3637 3643 3659 3671 3673 3677 3691 3697 3701 3709 3719 3727 3733 3739 3761 3767 3769 3779 3793 3797 3803 3821 3823 3833 3847 3851 3853 3863 3877 3881 3889 3907 3911 3917 3919 3923 3929 3931 3943 3947 3967 3989 4001 4003 4007 4013 4019 4021 4027 4049 4051 4057 4073 4079 4091 4093 4099 4111 4127 4129 4133 4139 4153 4157 4159 4177 4201 4211 4217 4219 4229 4231 4241 4243 4253 4259 4261 4271 4273 4283 4289 4297 4327 4337 4339 4349 4357 4363 4373 4391 4397 4409 4421 4423 4441 4447 4451 4457 4463 4481 4483 4493 4507 4513 4517 4519 4523 4547 4549 4561 4567 4583 4591 4597 4603 4621 4637 4639 4643 4649 4651 4657 4663 4673 4679 4691 4703 4721 4723 4729 4733 4751 4759 4783 4787 4789 4793 4799 4801 4813 4817 4831 4861 4871 4877 4889 4903 4909 4919 4931 4933 4937 4943 4951 4957 4967 4969 4973 4987 4993 4999 5003 5009 5011 5021 5023 5039 5051 5059 5077 5081 5087 5099 5101 5107 5113 5119 5147 5153 5167 5171 5179 5189 5197 5209 5227 5231 5233 5237 5261 5273 5279 5281 5297 5303 5309 5323 5333 5347 5351 5381 5387 5393 5399 5407 5413 5417 5419 5431 5437 5441 5443 5449 5471 5477 5479 5483 5501 5503 5507 5519 5521 5527 5531 5557 5563 5569 5573 5581 5591 5623 5639 5641 5647 5651 5653 5657 5659 5669 5683 5689 5693 5701 5711 5717 5737 5741 5743 5749 5779 5783 5791 5801 5807 5813 5821 5827 5839 5843 5849 5851 5857 5861 5867 5869 5879 5881 5897 5903 5923 5927 5939 5953 5981 5987 6007 6011 6029 6037 6043 6047 6053 6067 6073 6079 6089 6091 6101 6113 6121 6131 6133 6143 6151 6163 6173 6197 6199 6203 6211 6217 6221 6229 6247 6257 6263 6269 6271 6277 6287 6299 6301 6311 6317 6323 6329 6337 6343 6353 6359 6361 6367 6373 6379 6389 6397 6421 6427 6449 6451 6469 6473 6481 6491 6521 6529 6547 6551 6553 6563 6569 6571 6577 6581 6599 6607 6619 6637 6653 6659 6661 6673 6679 6689 6691 6701 6703 6709 6719 6733 6737 6761 6763 6779 6781 6791 6793 6803 6823 6827 6829 6833 6841 6857 6863 6869 6871 6883 6899 6907 6911 6917 6947 6949 6959 6961 6967 6971 6977 6983 6991 6997 7001 7013 7019 7027 7039 7043 7057 7069 7079 7103 7109 7121 7127 7129 7151 7159 7177 7187 7193 7207 7211 7213 7219 7229 7237 7243 7247 7253 7283 7297 7307 7309 7321 7331 7333 7349 7351 7369 7393 7411 7417 7433 7451 7457 7459 7477 7481 7487 7489 7499 7507 7517 7523 7529 7537 7541 7547 7549 7559 7561 7573 7577 7583 7589 7591 7603 7607 7621 7639 7643 7649 7669 7673 7681 7687 7691 7699 7703 7717 7723 7727 7741 7753 7757 7759 7789 7793 7817 7823 7829 7841 7853 7867 7873 7877 7879 7883 7901 7907 7919 7927 7933 7937 7949 7951 7963 7993 8009 8011 8017 8039 8053 8059 8069 8081 8087 8089 8093 8101 8111 8117 8123 8147 8161 8167 8171 8179 8191 8209 8219 8221 8231 8233 8237 8243 8263 8269 8273 8287 8291 8293 8297 8311 8317 8329 8353 8363 8369 8377 8387 8389 8419 8423 8429 8431 8443 8447 8461 8467 8501 8513 8521 8527 8537 8539 8543 8563 8573 8581 8597 8599 8609 8623 8627 8629 8641 8647 8663 8669 8677 8681 8689 8693 8699 8707 8713 8719 8731 8737 8741 8747 8753 8761 8779 8783 8803 8807 8819 8821 8831 8837 8839 8849 8861 8863 8867 8887 8893 8923 8929 8933 8941 8951 8963 8969 8971 8999 9001 9007 9011 9013 9029 9041 9043 9049 9059 9067 9091 9103 9109 9127 9133 9137 9151 9157 9161 9173 9181 9187 9199 9203 9209 9221 9227 9239 9241 9257 9277 9281 9283 9293 9311 9319 9323 9337 9341 9343 9349 9371 9377 9391 9397 9403 9413 9419 9421 9431 9433 9437 9439 9461 9463 9467 9473 9479 9491 9497 9511 9521 9533 9539 9547 9551 9587 9601 9613 9619 9623 9629 9631 9643 9649 9661 9677 9679 9689 9697 9719 9721 9733 9739 9743 9749 9767 9769 9781 9787 9791 9803 9811 9817 9829 9833 9839 9851 9857 9859 9871 9883 9887 9901 9907 9923 9929 9931 9941 9949 9967 9973 10007

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 12 2007, 06:07 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Gazoo @ Sep 11 2007, 10:32 PM) Creo que hay algun pequeño error de tipeo en el enunciado del problema , pues basta hacer a=0 y b=0 para que no se cumpla... pero imagino que es un detalle de tipeo que se le pasó a Luffy Upss, se me paso, gracias. 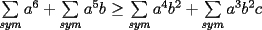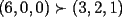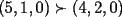lo arreglo altiro CITA(iMPuRe @ Sep 11 2007, 10:07 PM) Lo anterior por expansion, amplificacion por $TEX: $2$$ y cancelacion de terminos es equivalente a $TEX: $\sum\limits_{sym} {a^6}+\sum\limits_{sym} {a^5b} \ge \sum\limits_{sym} {a^4b^2}+\sum\limits_{sym} {a^3b^2c}$$ , y esto ultimo es cierto sumando las desigualdades de Muirhead para los vectores $TEX: $(6,0,0) \succ (3,2,1)$$ y $TEX: $(5,1,0) \succ (4,2,0)$$ . De que esta bien, esta bien, pero usar Muirhead no era la idea, el problema dice claramente que es para practicar Chebychev asi que no lo enviaré a resueltos hasta ver la solución con Chebychev (igual de simple y menos bruta). Saludos

The Lord Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 12 2007, 07:02 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Sin perdida de generalidad podemos asumir que $a\le b\le c$ (la desigualdad es simetrica).\\<br />Luego $a^2+ac\le b^2+bc \Rightarrow \dfrac{a}{b+c}\le\dfrac{b}{c+a}$; $b^2+ab\le c^2+ca \Rightarrow \dfrac{b}{c+a}\le\dfrac{c}{a+b}$, luego obtenemos:\\<br />$\dfrac{a}{b+c}\le\dfrac{b}{c+a} \le \dfrac{c}{a+b}$\\<br />Como se indicaba para este problema, ocupando la desigualdad de chebyshev:\\<br />$$\dfrac{{\left( {\sum {\dfrac{a}<br />{{b + c}}} } \right)\left( {\sum {a^3 } } \right)}}<br />{3} \leqslant \sum {\dfrac{{a^4 }}<br />{{b + c}}} $$\\<br />Donde $\dfrac{3}{2}\le {\sum {\dfrac{a}{{b + c}}} }$, reemplazando obtenemos lo pedido.\\<br />Saludos<br />$

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 12 2007, 07:12 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(The Lord @ Sep 12 2007, 08:02 PM) $TEX: \noindent Sin perdida de generalidad podemos asumir que $a\le b\le c$ (la desigualdad es simetrica).\\<br />Luego $a^2+ac\le b^2+bc \Rightarrow \dfrac{a}{b+c}\le\dfrac{b}{c+a}$; $b^2+ab\le c^2+ca \Rightarrow \dfrac{b}{c+a}\le\dfrac{c}{a+b}$, luego obtenemos:\\<br />$\dfrac{a}{b+c}\le\dfrac{b}{c+a} \le \dfrac{c}{a+b}$\\<br />Como se indicaba para este problema, ocupando la desigualdad de chebyshev:\\<br />$$\dfrac{{\left( {\sum {\dfrac{a}<br />{{b + c}}} } \right)\left( {\sum {a^3 } } \right)}}<br />{3} \leqslant \sum {\dfrac{{a^4 }}<br />{{b + c}}} $$\\<br />Donde $\dfrac{3}{2}\le {\sum {\dfrac{a}{{b + c}}} }$, reemplazando obtenemos lo pedido.\\<br />Saludos<br />$ Ahí si , y pasamos a resueltos PD: Uds. dediquense a resolver los más dificiles, dejen los básicos para los que esten empezando

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 9th April 2025 - 02:25 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.