|
|
|
|
|
|
|
  |
 Feb 5 2006, 06:53 AM Feb 5 2006, 06:53 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Estuve pensando mucho como enseñar esta seccion y la verdad me costo bastante tomar una decision(en el sentido de si hacerlo formal o informalmente) y decidi hacerlo informalmente(ojo que esto no significa en ningun sentido, incorrecto o menos valido) con la finalidad de que realmente entiendan de que se trata este llamativo y util tema.
"Seguramente para los que algo saben de el, les suena que hay que demostrar algo para el primer caso,y que se cumple para n,entonces para n+1 y listo". Pues bien....es muy facil decir que se sabe induccion pero no es tan facil decir que la entienden. Incluso es posible y es realmente facil demostrar cosas inductivamente sin entender ni un poquito de lo que se esta haciendo. Definiremos induccion simplemente como una manera de pensar. Esto quiere decir que les enseñare durante esta seccion a pensar "inductivamente" Entenderemos la idea a traves de los siguientes dos problemas: Problema 1 Consideremos un tablero cuadriculado de 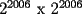 , al cual se le retira una esquina. , al cual se le retira una esquina.Demuestre que este tablero puede cubrirse totalmente (sin superposiciones y sin salir del tablero) utilizando fichas del siguiente tipo  que cubren exactamente 3 cuadraditos del tablero. Solucion: En la anterior demostracion reconocemos los siguientes elementos: 1)El comprobar que nuestra afirmacion es cierta en los primeros casos(en general se prueba en uno o dos casos, incluso mas, dependiendo del problema, la idea es probar casos particulares de nuestro problema hasta dar con la "regla de resolucion" de éste). En este caso lo probamos para los tableros de 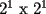 , , 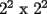 , , 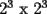 y y 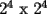 (¿sera necesario demostrarlo para tantos primeros casos?) (¿sera necesario demostrarlo para tantos primeros casos?)2)El crear el Paso Inductivo, que es aquel Metodo que nos permite afirmar lo siguiente: Si nuestro afirmacion para un cierto "n", entonces podriamos demostrar nuestra afirmacion para "n+1" En nuestro problema demostramos algo por el estilo: Si somos capaces de llenar un tablero de la forma 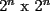 , entonces podriamos llenar un tablero de la forma , entonces podriamos llenar un tablero de la forma 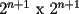 . .Pero esto justamente nos indica que si sabemos llenar el tablero de 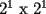 , entonces podriamos llenar el tablero de la forma , entonces podriamos llenar el tablero de la forma  . Pero como ahora podemos llenar el tablero de . Pero como ahora podemos llenar el tablero de 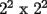 , entonces tambien podriamos llenar el tablero de , entonces tambien podriamos llenar el tablero de 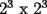 . Asi el razonamiento siempre se repite y en general la conclusion es que todos los tableros de la forma . Asi el razonamiento siempre se repite y en general la conclusion es que todos los tableros de la forma 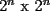 son llenables con las fichitas del enunciado. son llenables con las fichitas del enunciado.Si nos damos cuenta hemos razonado inductivamente en el sentido de que comprobamos un caso, luego el siguiente, y luego el siguiente del siguiente....y asi sucesivamente. Esto es algo que hacemos muy usualmente, por lo tanto la induccion no deberia parecerles algo tan raro. Este tipo de demostraciones se basa en apoyarse en los primeros pasos para que con esos podamos demostrar los pasos siguientes...y asi seguir avanzando. Tambien notamos que la "forma" de llenar un tablero de 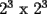 a partir del llenado del tablero de a partir del llenado del tablero de 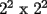 , es exactamente la misma "forma" de llenar el tablero de , es exactamente la misma "forma" de llenar el tablero de 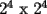 a partir del llenado del tablero de a partir del llenado del tablero de 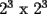 . O sea la estrategia para pasar de un tablero al siguiente de la serie, es SIEMPRE LA MISMA. Esto es justamente la gran gracia que deben cumplir los problemas que sean atacables por el metodo de induccion. Como todas las demostraciones son iguales, entonces basta hacer una, para asi tenerlas todas(esta idea la maduraremos mas adelante). . O sea la estrategia para pasar de un tablero al siguiente de la serie, es SIEMPRE LA MISMA. Esto es justamente la gran gracia que deben cumplir los problemas que sean atacables por el metodo de induccion. Como todas las demostraciones son iguales, entonces basta hacer una, para asi tenerlas todas(esta idea la maduraremos mas adelante).Problema 2 Calcule el valor de: 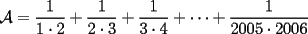 Solucion: Breves comentarios que nunca esta de mas leer Para mi este problema fue muy especial pues a pesar de ser tan simple y facil, me dejo una gran moraleja sobre el significado de la induccion y en realidad para que "me servia a mi" saber induccion. Me di cuenta que yo podria intuir una regla general para algun problema, entonces podria eventualmente intentar demostrarla por induccion(una vez encontrada aquella regla general, que en este problema salia muy intuitiva). Tambien gane otra intuicion que quizas no tenia tanto que ver con induccion pero era el hecho de que a veces cuando uno se enfrenta a un problema aparentemente monstruoso, una opcion es resolver el problema en situaciones mas simples, tratar de resolver problemas mas "chiquititos" y de ahi sacar conclusiones para el problema mayor. Increiblemente despues de entender esto me salieron muchos problemas que antes no habia caso que se me ocurrieran. Despues entendi mas alla eso de que la induccion es una "forma de pensar", con problemas que me hicieron notar que no basta solo probar un caso porque la induccion no "podia echarla a andar", despues descubri que habian problemas donde lo mas dificil era el primer caso, y no la induccion("el paso inductivo") en si. Tambien me di cuenta que la induccion indica pensar de alguien en el siguiente, pero puedo hacerlo a mi pinta, o sea de un numero a su doble(fijense el en ejemplo 1) o bien quizas demostrar que si se cumple en cierto instante, entonces se cumple para el anterior(cosas locas que en realidad me hacen sentir libre de aplicar la induccion en la forma que se me de la regalada gana). Tambien comprendi que a veces hay problemas que necesitan de demostrar otro problema por induccion, y una induccion permite realizar la otra induccion. Tambien inducciones de varias variables al mismo tiempo, o bien inducciones donde se prueba conjuntamente mas de una propiedad (y que aquellas propiedades por separado no son demostrables por induccion) y asi muchas mas...asi que este tema da para muuuuuuuucho mas que demostrar que si "algo se cumple para n, entonces para n+1"(nuestra frase al partir esta leccion) PD: Al momento que ustedes suponen que la propiedad se cumple para "algun n" no estan cometiendo ningun pecado pues hay "n" donde la propiedad si es cierta, o sea por ejemplo el(los) primer(os) caso(s) que hayan demostrado. Tambien cabe mencionar que se le denomina Hipotesis de Induccion a esa suposicion. PD: No crean que al realizar la Hipotesis de Induccion estan suponiendo lo que quieren demostrar, porque no es lo mismo suponer que se cumple para "algun n", que decir que se cumple "para todo n". A estudiar...a estudiar -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 22 2006, 11:55 AM Feb 22 2006, 11:55 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 1
Probar que la expresion 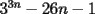 es un multiplo de es un multiplo de 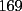 para todo para todo 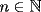 . .Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 22 2006, 12:36 PM Feb 22 2006, 12:36 PM
Publicado:
#3
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 2
Probar que: 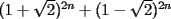 es un entero par y que ademas: 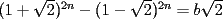 para algun 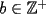 , para todo entero , para todo entero 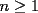 . .Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 22 2006, 03:03 PM Feb 22 2006, 03:03 PM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 3
Probar que si "  " es impar, entonces " es impar, entonces 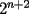 divide a divide a 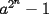 para todo entero para todo entero 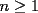 . .Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 22 2006, 04:33 PM Feb 22 2006, 04:33 PM
Publicado:
#5
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 4 (Olimpiada Estadounidense,1978)
Un entero  es llamado "bueno" si nosotros se cumple que: es llamado "bueno" si nosotros se cumple que: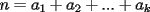 donde 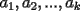 son enteros positivos(no necesariamente distintos) que satisfacen: son enteros positivos(no necesariamente distintos) que satisfacen: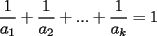 Si es sabido que los enteros desde 33 hasta 73 son "buenos", entonces probar que todo entero mayor o igual que 33 es "bueno". Solucion: -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Mar 12 2006, 03:29 PM Mar 12 2006, 03:29 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
CITA(Kenshin @ Feb 22 2006, 12:55 PM) Cómo factorizas?? 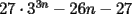 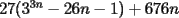 Otra cosa creo que hay un pequeño error de tipeo donde N=1.... -------------------- |
|
|
|
 Mar 12 2006, 07:35 PM Mar 12 2006, 07:35 PM
Publicado:
#7
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 361 Registrado: 24-September 05 Desde: beaucheff #850 Stgo Miembro Nº: 324 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA(caf_tito @ Mar 12 2006, 04:29 PM) 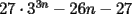 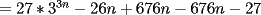 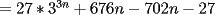 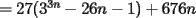 eso creo que es lo que hizo -------------------- Súmese a la campaña de conciencia energética
 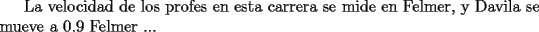 |
|
|
|
 Mar 12 2006, 07:45 PM Mar 12 2006, 07:45 PM
Publicado:
#8
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 414 Registrado: 19-May 05 Desde: puente alto, santiago Miembro Nº: 45 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Muchas gracias por haber notado el error al escribir los indices.
Lo que hice para que la demostración estuviese totalmente correcta, modifique el enunciado a: Probar que la expresión 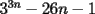 es un multiplo de es un multiplo de 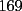 para todo para todo 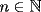 . .con eso el caso base permance igual, la hipótesis de inducción debio ser modificada en su segunda línea y la demostracion quedo intacta. Bajo ningún punto de vista, quiero hacer notar, que cambie el problema en sí, ya que es cosa de ver que con el enunciado anterior 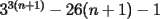 la propiedad se cumplia incluso para la propiedad se cumplia incluso para 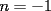 , es decir, se podia mover el n hasta dos unidades y la propiedad seguirá siendo cierta (considerando los naturales desde el 1). , es decir, se podia mover el n hasta dos unidades y la propiedad seguirá siendo cierta (considerando los naturales desde el 1).es decir el enunciado perfectamente pudo ser 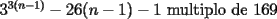 , pero lo deje así para que calzara totalmente con la demostracion, y el problema no cambio. , pero lo deje así para que calzara totalmente con la demostracion, y el problema no cambio.Sobre lo de la factorizacion, date cuenta que 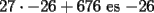 eso es todo. Tal como dice Milo eso es todo. Tal como dice MiloFrancisco Muñoz Espinoza -------------------- "No tenemos la solucion a todos los problemas del mundo en nuestras manos... Pero frente a los problemas del mundo tenemos nuestras manos..."
Teresa de Calcuta |
|
|
|
 Mar 18 2006, 04:13 PM Mar 18 2006, 04:13 PM
Publicado:
#9
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Bueno, creo que logicamente ese era el enunciado que yo aspiraba..jejejeje.
Entre tanto que escribi seguido en aquellos tiempos, se me paso de largo..asi que agradezco la correcion y eso me indica que no solo leen la solucion sino que buscan entenderla completamente. Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jun 11 2006, 04:08 PM Jun 11 2006, 04:08 PM
Publicado:
#10
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo:  Universidad:  Sexo:  |
una consulta sobre la última demostración que hizo kenshin
![TEX: \[<br />P\left( {n + 1} \right)<br />\]](./tex/77927.gif) se referiere a 2n+8,2n+9,...etc ?? se referiere a 2n+8,2n+9,...etc ??segundo se supone que en la hipótesis de inducción en ese caso es que ![TEX: \[<br />P\left( n \right)<br />\]](./tex/77928.gif) y lo que queda por demostrar es el lema que ya está demostrado, cierto?. -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th October 2025 - 08:19 AM |






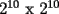 tiene mas de un millon de cuadraditos. Esto pues
tiene mas de un millon de cuadraditos. Esto pues 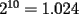 y por ende
y por ende 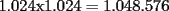 cuadraditos, pero como por enunciado al tablero le falta una esquina, entonces tendra
cuadraditos, pero como por enunciado al tablero le falta una esquina, entonces tendra 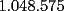 cuadraditos, a llenar con fichas del estilo mencionado en el enunciado
cuadraditos, a llenar con fichas del estilo mencionado en el enunciado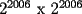 ...realmente imposible si pensamos
...realmente imposible si pensamos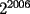 es igual a:
es igual a: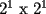 sin una esquina
sin una esquina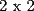 y sin una esquina. Esto es:
y sin una esquina. Esto es:
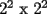 sin una esquina
sin una esquina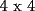 y sin una esquina. Esto es:
y sin una esquina. Esto es:

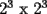 sin una esquina
sin una esquina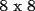 y sin una esquina. Esto es:
y sin una esquina. Esto es:
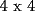 sin una esquina... realizaremos el llenado de este nuevo tablero basados en el llenado anterior(pues intentar llenarlo solo probando se vuelve algo mas dificil en este caso). Esto lo haremos de la siguiente forma.
sin una esquina... realizaremos el llenado de este nuevo tablero basados en el llenado anterior(pues intentar llenarlo solo probando se vuelve algo mas dificil en este caso). Esto lo haremos de la siguiente forma.
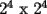 sin una esquina
sin una esquina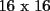 y sin una esquina. Esto es:
y sin una esquina. Esto es:
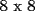 sin una esquina... Esto lo haremos de la siguiente forma.
sin una esquina... Esto lo haremos de la siguiente forma.
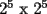 y
y 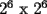 y asi sucesivamente?
y asi sucesivamente?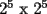 o
o 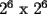 sino que cualquier tablero de la forma
sino que cualquier tablero de la forma 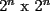 (por supuesto, que le falte una punta) a partir del tablero de
(por supuesto, que le falte una punta) a partir del tablero de 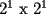 (
( 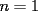 ) que fue nuestro primer tablero.
) que fue nuestro primer tablero. 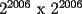 siguiendo nuestro "metodo inductivo"
siguiendo nuestro "metodo inductivo"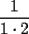 , Tendremos entonces que hasta ahi la suma es
, Tendremos entonces que hasta ahi la suma es 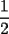
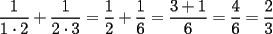
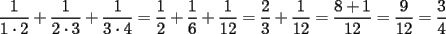
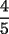 , y en general, si sumamos los n primeros terminos nos dara
, y en general, si sumamos los n primeros terminos nos dara 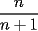 ( por supuesto se concluiria que en particular el resultado de nuestro problema seria
( por supuesto se concluiria que en particular el resultado de nuestro problema seria 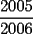 )
)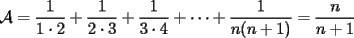
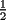 , nos gustaria una forma de probar que con dos sumandos la suma es
, nos gustaria una forma de probar que con dos sumandos la suma es 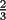 , y a partir de eso poder concluir que con tres sumandos sera
, y a partir de eso poder concluir que con tres sumandos sera 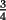 , y asi sucesivamente.
, y asi sucesivamente.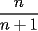 , entonces la suma de "n+1 sumandos" sera
, entonces la suma de "n+1 sumandos" sera 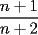
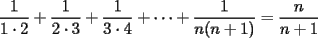
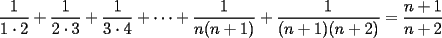
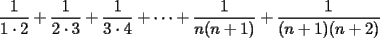
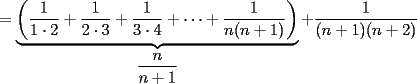
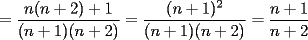
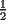 , entonces la suma con dos terminos sera
, entonces la suma con dos terminos sera 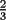 (esto usando la propiedad de pasaje), pero entonces como la suma con 2 terminos es
(esto usando la propiedad de pasaje), pero entonces como la suma con 2 terminos es 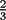 , podemos invocar nuevamente a la propiedad de pasaje y concluir que la suma con tres terminos vale
, podemos invocar nuevamente a la propiedad de pasaje y concluir que la suma con tres terminos vale 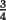 , y se sigue asi sucesivamente, logrando demostrar la propiedad para todos los n enteros mayores o iguales que 1.
, y se sigue asi sucesivamente, logrando demostrar la propiedad para todos los n enteros mayores o iguales que 1.



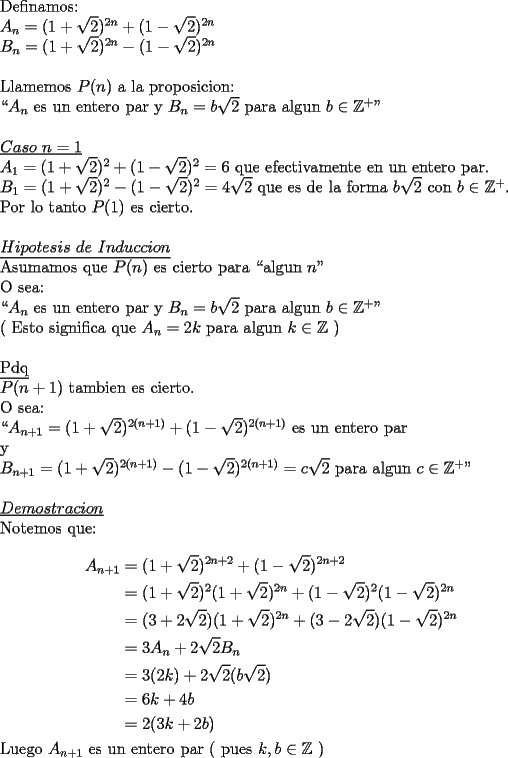


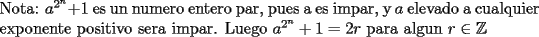


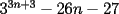 es un multiplo de
es un multiplo de 
