Tecnica Especial - Foro fmat.cl

Tecnica Especial, Resuelto por Caetano

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 3 2006, 03:23 AM Publicado: #1
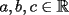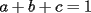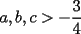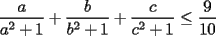Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	Problema Probar que si $TEX: $a,b,c\in\mathbb{R}$$ cumplen que $TEX: $a+b+c=1$$ y $TEX: $\displaystyle a,b,c>-\frac{3}{4}$$ entonces: $TEX: $\displaystyle \frac{a}{a^2+1}+\frac{b}{b^2+1}+\frac{c}{c^2+1}\le<br />\frac{9}{10}$$ Fuente: Poland 1996 Solucion: Notemos que: 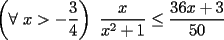$TEX: $\displaystyle \left(\forall\ x>-\frac{3}{4}\right)\ \frac{x}{x^2+1}\le \frac{36x+3}{50}$$ pues a traves de un desarrollo algebraico observamos que : 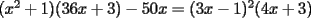$TEX: $(x^2+1)(36x+3)-50x=(3x-1)^2(4x+3)$$ lo cual es no negativo para $TEX: $\displaystyle x>-\frac{3}{4}$$ , y por lo tanto: $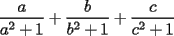TEX: $\displaystyle \frac{a}{a^2+1}+\frac{b}{b^2+1}+\frac{c}{c^2+1}$$ $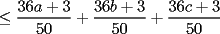TEX: $\displaystyle\le \frac{36a+3}{50}+\frac{36b+3}{50}+\frac{36c+3}{50}$$ $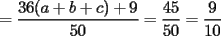TEX: $\displaystyle =\frac{36(a+b+c)+9}{50}=\frac{45}{50}=\frac{9}{10}$$ concluyendo lo pedido Resuelto por Caetano -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)