Examen - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Media > Escuela de Verano > Escuela de Verano > Matemática > Matemáticas III

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Examen, Matemáticas III 2008

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2008, 10:26 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	Como me motivé debido a que publicaron las secciones de la universidad, aquí va el examen cabros Aprobé el curso son 5.8 =) $TEX: \noindent \fbox{P1} \\<br />\noindent (a) Calcule, usando la definici\'on, las derivadas de las siguientes funciones: \\<br /><br />\indent (i) $f(x)=x+\operatorname{sen}(2x)$ \\<br />\indent (ii) $g(x)=(x+1)^2 -2x$ \\<br /><br />\noindent (b) Calcule, usando las reglas estudiadas, las derivadas de las siguientes funciones:\\<br />\indent (i) $e^{\operatorname{sen}(x^2+1)}+\ln (\cos (\sqrt{x}))$ \\<br />\indent (ii) $x^{\sin x}\tan (3x^3+2)$ \\<br /><br />\noindent \fbox{P2}<br /><br />Sea la función :<br />$$f(x)= \begin{cases}<br />e^x - 1\qquad \qquad \text{si }x\in (-\infty ,-2)\\<br />\dfrac{1}{\cos \left( \frac{\pi}{4}x \right)}-1\quad \text{si }x\in (-2,2)\\<br />-\dfrac{2}{(2-x)^2} \qquad \text{si }x\in (2,+\infty )<br />\end{cases}$$ \\<br />\indent (i) Para $f$ determine dominio, ceros, continuidad, encuentre sus asíntotas, si las tiene, y para cada punto $x_0 \in \mathbb R$ donde la funci\'on no se ha definido, determine si es posible asignar un valor a $f(x_0)$ de modo que $f$ sea continua en $x_0$$ $TEX: \indent Dado que:<br />$$f'(x)= \begin{cases}<br />e^x \qquad \qquad \qquad \qquad \text{si }x\in (-\infty ,-2)\\<br />\dfrac{\pi}{4\cos^2 (\frac \pi 4 x)}\cdot \operatorname{sen}\frac \pi 4 x \quad \text{si }x\in (-2,2)\\<br />-\dfrac{2}{(2-x)^3} \quad \qquad \qquad \text{si }x\in (2,+\infty )<br />\end{cases}$$ \\<br /><br />\indent Y además:<br />$$f''(x)= \begin{cases}<br />e^x \qquad \qquad \qquad \qquad \text{si }x\in (-\infty ,-2)\\<br />\dfrac{\pi^2}{16}\cdot \dfrac{1+\operatorname{sen}^2 (\frac \pi 4 x)}{\cos^3 (\frac \pi 4 x)}\cdot \operatorname{sen}\frac \pi 4 x \quad \text{si }x\in (-2,2)\\<br />-\dfrac{6}{(2-x)^4} \quad \qquad \qquad \text{si }x\in (2,+\infty )<br />\end{cases}$$ \\<br />$\textbf{Nota: }$ Observe que $no$ se le pide calcular estas derivadas\\<br /><br />\indent (ii) Estudie el crecimiento de $f$ y encuentre sus máximos y mínimos (si es que los tiene).\\<br />\indent (iii) Estudie la concavidad de $f$ e indique sus puntos de inflexión (si es que los tiene).\\<br />\indent (iv) Bosqueje el gráfico de la función utilizando el análisis procedente.$ $TEX: \noindent \fbox{P3}\\<br /><br />\noindent (a) Considere la siguiente ecuación: \\<br />$$x^{139}+x^{60}+1+\operatorname{sen}(x) =x \qquad \qquad (1)$$\\<br />\indent (i) Para la función $g(x)=x^{139}+x^{60}+1+\operatorname{sen}(x)-x$ definida $\forall x\in \mathbb R$: \\<br />\indent \quad (i.1) Muestre que $(\exists M>0)\ g(M)>0.$ Ind: Calcule $\displaystyle \lim_{x\to \infty} g(x)$ \\<br />\indent \quad (i.2) Muestre que $(\exists m<0)\ g(m)<0$\\<br />\indent (ii) Muestre que existe $c\in \mathbb R$ solución de la ecuación (1). \\<br /><br />\noindent (b) Con los pasos siguientes usted demostrar (debería decir "deberá demostrar") la desigualdad $e^x\ge 1+x+\dfrac{x^2}{2}$ para $x\ge 0$\\<br /><br />\indent (i) Considere la función $h(x)=e^x-1-x-\dfrac{x^2}{2}$ y pruebe que\\<br />$(\forall x\in \mathbb R )\ h'(x) \ge 0$\\<br />\indent (ii) Pruebe que $(\forall x\in [0,+\infty[)(\exists \xi \in \ ]0,x[) \ h(x)=h'(\xi)x$ \\<br />\indent (iii) Concluya la desigualdad pedida.$ --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 24 2008, 10:28 PM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	Algunos hints.... P3... Parte (a) usar TVI (Teorema del valor Intermedio) Parte (b) usar TVM (Teorema del valor Medio) P1... Recordar fórmulas de la suma de coseno y seno (de ahí puede concluir la de ángulo doble) Además, recordar los límites conocidos de seno y coseno --------------------

Eguvi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 25 2008, 11:49 AM Publicado: #3
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 944 Registrado: 25-January 07 Desde: Av. España #1680 - Valparadisee :P Miembro Nº: 3.878 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\boxed{\mathcal{Sp}_{1a}}$$ ii) $TEX: % MathType!Translator!2!1!LaTeX.tdl!TeX -- LaTeX 2.09 and later!<br />% MathType!MTEF!2!1!+-<br />% feqaeaartrvr0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l<br />% bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R<br />% Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa<br />% caGaaeqabaaaamaaaOabaeqabaGaamOzaiaacIcacaWG4bGaaiykai<br />% abg2da9maavacabeWcbeqaaiaaikdaa0qaamaabmaabaGaamiEaiab<br />% gUcaRiaaigdaaiaawIcacaGLPaaaaaGccqGHsislcaaIYaGaamiEai<br />% abg2da9maavacabeWcbeqaaiaaikdaa0qaaiaadIhaaaGccqGHRaWk<br />% caaIXaaabaaabaWaaSaaaeaacaWGKbGaamOzaaqaaiaadsgacaWG4b<br />% aaaiaacIcacaWG4bGaaiykaiabg2da9maaxababaGaciiBaiaacMga<br />% caGGTbaaleaacaWGObGaeyOKH4QaaGimaaqabaGcdaWcaaqaamaabm<br />% aabaWaaubiaeqaleqabaGaaGOmaaqdbaWaaeWaaeaacaWG4bGaey4k<br />% aSIaamiAaaGaayjkaiaawMcaaaaakiabgUcaRiaaigdaaiaawIcaca<br />% GLPaaacqGHsisldaqadaqaamaavacabeWcbeqaaiaaikdaa0qaaiaa<br />% dIhaaaGccqGHRaWkcaaIXaaacaGLOaGaayzkaaaabaGaamiAaaaaae<br />% aaaeaadaWcaaqaaiaadsgacaWGMbaabaGaamizaiaadIhaaaGaaiik<br />% aiaadIhacaGGPaGaeyypa0ZaaCbeaeaaciGGSbGaaiyAaiaac2gaaS<br />% qaaiaadIgacqGHsgIRcaaIWaaabeaakmaalaaabaWaaubiaeqaleqa<br />% baGaaGOmaaqdbaGaamiEaaaakiabgUcaRiaaikdacaWG4bGaamiAai<br />% abgUcaRmaavacabeWcbeqaaiaaikdaa0qaaiaadIgaaaGccqGHRaWk<br />% caaIXaGaeyOeI0YaaubiaeqaleqabaGaaGOmaaqdbaGaamiEaaaaki<br />% abgkHiTiaaigdaaeaacaWGObaaaaqaaaqaamaalaaabaGaamizaiaa<br />% dAgaaeaacaWGKbGaamiEaaaacaGGOaGaamiEaiaacMcacqGH9aqpda<br />% WfqaqaaiGacYgacaGGPbGaaiyBaaWcbaGaamiAaiabgkziUkaaicda<br />% aeqaaOWaaSaaaeaacaWGObWaaeWaaeaacaaIYaGaamiEaiabgUcaRi<br />% aadIgaaiaawIcacaGLPaaaaeaacaWGObaaaiabg2da9iaaikdacaWG<br />% 4bGaey4kaSIaamiAaiabgkDiElaaikdacaWG4bGaey4kaSIaaGimai<br />% abg2da9iaaikdacaWG4baaaaa!9F8D!<br />\[<br />\begin{array}{l}<br /> g(x) = \mathop {\left( {x + 1} \right)}\nolimits^2 - 2x = \mathop x\nolimits^2 + 1 \\ <br /> \\ <br /> \dfrac{{dg}}{{dx}}(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{\left( {\mathop {\left( {x + h} \right)}\nolimits^2 + 1} \right) - \left( {\mathop x\nolimits^2 + 1} \right)}}{h} \\ <br /> \\ <br /> \dfrac{{dg}}{{dx}}(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{\mathop x\nolimits^2 + 2xh + \mathop h\nolimits^2 + 1 - \mathop x\nolimits^2 - 1}}{h} \\ <br /> \\ <br /> \dfrac{{dg}}{{dx}}(x) = \mathop {\lim }\limits_{h \to 0} \dfrac{{h\left( {2x + h} \right)}}{h} = 2x + h \Rightarrow 2x + 0 = 2x \\ <br /> \end{array}<br />\]<br />$ Mensaje modificado por Eguvi el Jan 25 2008, 05:43 PM -------------------- Estudiante de Ing. Civil Industrial - III año Universidad Técnica Federico Santa María CITA(egadobkn @ Mar 24 2010, 06:45 PM) olaaa me llamo edgardo y me la como atravesá =P=P=P=P

Eguvi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 25 2008, 11:51 AM Publicado: #4
Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 944 Registrado: 25-January 07 Desde: Av. España #1680 - Valparadisee :P Miembro Nº: 3.878 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\boxed{\mathcal{Sp}_{1b}}$$ i) $TEX: % MathType!Translator!2!1!LaTeX.tdl!TeX -- LaTeX 2.09 and later!<br />% MathType!MTEF!2!1!+-<br />% feqaeaartrvr0aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaebbnrfifHhDYfgasaacH8srps0l<br />% bbf9q8WrFfeuY-Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0R<br />% Yxir-Jbba9q8aq0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGa<br />% caGaaeqabaaaamaaaOabaeqabaGaamiAaiaacIcacaWG4bGaaiykai<br />% abg2da9maavacabeWcbeqaaiGacohacaGGPbGaaiOBamaabmaabaWa<br />% aubiaeqameqabaGaaGOmaaGdbaGaamiEaaaaliabgUcaRiaaigdaai<br />% aawIcacaGLPaaaa0qaaiaadwgaaaGccqGHRaWkciGGSbGaaiOBamaa<br />% bmaabaGaci4yaiaac+gacaGGZbWaaeWaaeaadaGcaaqaaiaadIhaaS<br />% qabaaakiaawIcacaGLPaaaaiaawIcacaGLPaaaaeaaaeaacqGHshI3<br />% caWGObGaai4jaiaacIcacaWG4bGaaiykaiabg2da9maavacabeWcbe<br />% qaaiGacohacaGGPbGaaiOBamaabmaabaWaaubiaeqameqabaGaaGOm<br />% aaGdbaGaamiEaaaaliabgUcaRiaaigdaaiaawIcacaGLPaaaa0qaai<br />% aadwgaaaGccaGG3cGaci4yaiaac+gacaGGZbWaaeWaaeaadaqfGaqa<br />% bSqabeaacaaIYaaaneaacaWG4baaaOGaey4kaSIaaGymaaGaayjkai<br />% aawMcaaiaacElacaaIYaGaamiEaiabgUcaRmaalaaabaWaaeWaaeaa<br />% cqGHsislciGGZbGaaiyAaiaac6gadaqadaqaamaakaaabaGaamiEaa<br />% WcbeaaaOGaayjkaiaawMcaaaGaayjkaiaawMcaaaqaaiGacogacaGG<br />% VbGaai4CamaabmaabaWaaOaaaeaacaWG4baaleqaaaGccaGLOaGaay<br />% zkaaGaai4TaiaaikdadaGcaaqaaiaadIhaaSqabaaaaaGcbaaabaGa<br />% amiAaiaacEcacaGGOaGaamiEaiaacMcacqGH9aqpdaqfGaqabSqabe<br />% aaciGGZbGaaiyAaiaac6gadaqadaqaamaavacabeadbeqaaiaaikda<br />% a4qaaiaadIhaaaWccqGHRaWkcaaIXaaacaGLOaGaayzkaaaaneaaca<br />% WGLbaaaOGaai4TaiGacogacaGGVbGaai4CamaabmaabaWaaubiaeqa<br />% leqabaGaaGOmaaqdbaGaamiEaaaakiabgUcaRiaaigdaaiaawIcaca<br />% GLPaaacaGG3cGaaGOmaiaadIhacqGHsisldaWcaaqaaiGacshacaGG<br />% HbGaaiOBamaabmaabaWaaOaaaeaacaWG4baaleqaaaGccaGLOaGaay<br />% zkaaaabaGaaGOmamaakaaabaGaamiEaaWcbeaaaaaaaaa!9A86!<br />\[<br />\begin{array}{l}<br /> h(x) = \mathop e\nolimits^{\sin \left( {\mathop x\nolimits^2 + 1} \right)} + \ln \left( {\cos \left( {\sqrt x } \right)} \right) \\ <br /> \\ <br /> \Rightarrow h'(x) = \mathop e\nolimits^{\sin \left( {\mathop x\nolimits^2 + 1} \right)} \cdot\cos \left( {\mathop x\nolimits^2 + 1} \right)\cdot2x + \dfrac{{\left( { - \sin \left( {\sqrt x } \right)} \right)}}{{\cos \left( {\sqrt x } \right)\cdot2\sqrt x }} \\ <br /> \\ <br /> h'(x) = \mathop e\nolimits^{\sin \left( {\mathop x\nolimits^2 + 1} \right)} \cdot\cos \left( {\mathop x\nolimits^2 + 1} \right)\cdot2x - \dfrac{{\tan \left( {\sqrt x } \right)}}{{2\sqrt x }} \\ <br /> \end{array}<br />\]<br />$ Mensaje modificado por Eguvi el Jan 25 2008, 11:58 AM -------------------- Estudiante de Ing. Civil Industrial - III año Universidad Técnica Federico Santa María CITA(egadobkn @ Mar 24 2010, 06:45 PM) olaaa me llamo edgardo y me la como atravesá =P=P=P=P

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 28 2008, 11:21 AM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	Motivao: $TEX: \noindent \fbox{Sol P1-b-ii}\\<br />\begin{equation}<br />\begin{aligned}<br />\text{Sea }r &= x^{\sin x} \qquad \big/ \ln ()\\<br />\ln r &= \ln (x^{\sin x})\\<br />\ln r &= \sin x \cdot \ln x \qquad \big/ \operatorname{exp} ()\\<br />r &= \operatorname{exp} (\sin x \cdot \ln x)<br />\end{aligned}<br />\end{equation}<br /><br />Sean también\\<br />$u=\operatorname{exp} (\sin x \cdot \ln x)$\\<br />$v=\tan (3x^3+2)$ \\<br /><br />La solución a esto está dada por<br />$u'v+uv'$ así que desarrollamos\\<br /><br />\noindent $S=\operatorname{exp} (\sin x \cdot \ln x)\cdot \left[ \cos x\cdot \ln x + \dfrac{\sin x}{x} \right] \cdot \tan (3x^3+2) + \operatorname{exp} (\sin x \cdot \ln x)\cdot \sec^2 (3x^3+2)\cdot 9x^2$\\<br /><br />Esto parece bastante horroroso así que volveremos a la forma original:\\<br /><br />\noindent $S=x^{\sin x}\cdot \left[ \cos x\cdot \ln x + \dfrac{\sin x}{x} \right] \cdot \tan (3x^3+2) + x^{\sin x}\cdot \sec^2 (3x^3+2)\cdot 9x^2$\\\\$ --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 12:27 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	CITA(Ictio @ Jan 25 2008, 01:26 AM) $TEX: \noindent \fbox{P3-b-ii}\\<br /><br />$h(x)=e^x-1-x-\dfrac{x^2}{2}$\\<br />\indent (ii) Pruebe que $(\forall x\in [0,+\infty[)(\exists \xi \in \ ]0,x[) \ h(x)=h'(\xi)x$ \\<br />$ Observemos que las funciones $TEX: $$e^x,\ -1,\ -x,\ -\ \dfrac{x^2}{2}$$<br />Son continuas en todo su dominio y por $h(x)$ ser suma y resta de estas funciones, es continua en todo su dominio. También logramos ver que si $h$ es continua en $[0,\infty[$ entonces claramente lo es en $]0,x[$. Así, gratamente para nosotros podemos usar el siempre bien ponderado \fbox{Teorema del Valor Medio} ya que $h$ es continua en $[0,x]$ y derivable en $]0,x[$ ya que su gráfico no parece tener "puntas", es decir, su curva parece ser suave (nunca entendí bien el argumento de por qué una función es derivable..\\<br />\fbox{NOTA: con $b=x$ y $a=0$}<br /><br />$$h'(\xi)=\dfrac{h(x) - h(0)}{x-0}$$<br />guau!, pero $h(0)=0$<br />$$h'(\xi)=\dfrac{h(x)}{x}$$\\<br />Con lo que se concluye lo pedido$ Lo malo de esto es que: No se me ocurrió en el examen --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 20 2008, 11:06 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	Pregunta Leech Alguien se motiva a responder algunas de las que no están resueltas? --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 1 2008, 09:54 PM Publicado: #8
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	$TEX: \noindent \fbox{P3.b i)}\\<br />Recordemos que la desigualdad fundamental de la exponencial nos dice que:<br />$$e^x\ge 1+x.$$<br />Ahora notemos que $\dfrac{dh}{dx}=e^x-x-1$. Es directo de la desigualdad fundamental que<br />$$\dfrac{dh}{dx}\ge 0$$<br />Demostrando lo pedido pues:<br />$$\dfrac{dh}{dx}=e^x-1-x$$$ Saludos y motivense!!! --------------------

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jun 1 2008, 10:37 PM Publicado: #9
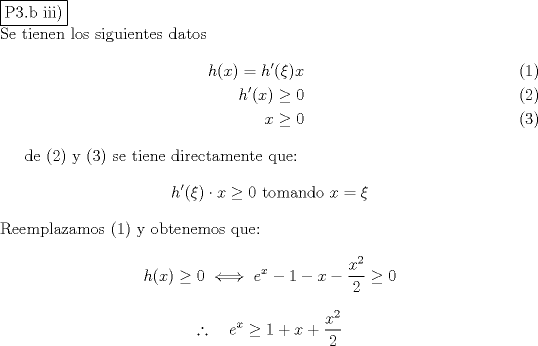
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	$TEX: \noindent \fbox{P3.b iii)}\\<br />Se tienen los siguientes datos<br />\begin{eqnarray}<br />h(x) = h'(\xi )x \\<br />h'(x) \ge 0 \\<br />x\ge 0<br />\end{eqnarray}<br /><br />de (2) y (3) se tiene directamente que:<br />$$h'(\xi ) \cdot x \ge 0\ \text{tomando }x=\xi$$<br />Reemplazamos (1) y obtenemos que:<br />$$h(x)\ge 0 \iff e^x-1-x-\dfrac{x^2}{2} \ge 0$$<br />$$\therefore \quad e^x \ge 1+x+\dfrac{x^2}{2}$$$ --------------------

nico92 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 17 2009, 10:04 PM Publicado: #10
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 9-January 09 Miembro Nº: 41.876 Sexo:	wena muy weno

« Posterior · Matemáticas III · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 24th November 2024 - 02:47 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.