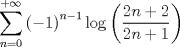Propuesto 9 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Cálculo > Series

Reply to this topic

Start new topic

Propuesto 9, simpático y bonito

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 20 2008, 07:49 PM Publicado: #1
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	$TEX: \noindent Expresar$$\int_0^1 {\frac{{1 - u}}<br />{{\left( {1 + u^2 } \right)\ln u}}\,du}$$$ $TEX: \noindent como una suma infinita.$ Suerte

master_c	Mar 16 2013, 05:17 PM Publicado: #2
Invitado	¿Nadie se motiva? para el que quiera intentarlo $TEX: $$<br />\sum\limits_{n = 0}^{ + \infty } {\left( { - 1} \right)^{n - 1} \log \left( {\frac{{2n + 2}}<br />{{2n + 1}}} \right)} <br />$$$ Mensaje modificado por master_c el Mar 29 2013, 02:19 PM

「Krizalid」 Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 16 2013, 05:54 PM Publicado: #3
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo:	No es difícil, está para soltar la mano.

master_c	Mar 16 2013, 07:31 PM Publicado: #4
Invitado	CITA(「Krizalid」 @ Mar 16 2013, 05:54 PM) No es difícil, está para soltar la mano. 4 años y meses y nadie se motiva fmat ya no es lo mismo de antes

master_c	Mar 29 2013, 02:19 PM Publicado: #5
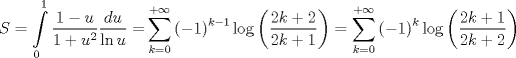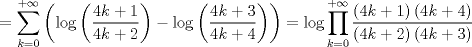Invitado	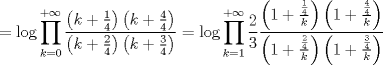$TEX: $$<br />S = \int\limits_0^1 {\frac{{1 - u}}<br />{{1 + u^2 }}\frac{{du}}<br />{{\ln u}} = } \sum\limits_{k = 0}^{ + \infty } {\left( { - 1} \right)^{k - 1} \log \left( {\frac{{2k + 2}}<br />{{2k + 1}}} \right)} = \sum\limits_{k = 0}^{ + \infty } {\left( { - 1} \right)^k \log \left( {\frac{{2k + 1}}<br />{{2k + 2}}} \right)} <br />$$$ $TEX: $$<br /> = \sum\limits_{k = 0}^{ + \infty } {\left( {\log \left( {\frac{{4k + 1}}<br />{{4k + 2}}} \right) - \log \left( {\frac{{4k + 3}}<br />{{4k + 4}}} \right)} \right)} = \log \prod\limits_{k = 0}^{ + \infty } {\frac{{\left( {4k + 1} \right)\left( {4k + 4} \right)}}<br />{{\left( {4k + 2} \right)\left( {4k + 3} \right)}}} <br />$$$ $TEX: $$<br /> = \log \prod\limits_{k = 0}^{ + \infty } {\frac{{\left( {k + \frac{1}<br />{4}} \right)\left( {k + \frac{4}<br />{4}} \right)}}<br />{{\left( {k + \frac{2}<br />{4}} \right)\left( {k + \frac{3}<br />{4}} \right)}}} = \log \prod\limits_{k = 1}^{ + \infty } {\frac{2}<br />{3}\frac{{\left( {1 + \frac{{\frac{1}<br />{4}}}<br />{k}} \right)\left( {1 + \frac{{\frac{4}<br />{4}}}<br />{k}} \right)}}<br />{{\left( {1 + \frac{{\frac{2}<br />{4}}}<br />{k}} \right)\left( {1 + \frac{{\frac{3}<br />{4}}}<br />{k}} \right)}}} <br />$$$ recordando la definicion de funcion gamma en su forma de producto 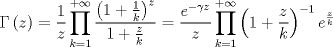$TEX: $$<br />\Gamma \left( z \right) = \frac{1}<br />{z}\prod\limits_{k = 1}^{ + \infty } {\frac{{\left( {1 + \frac{1}<br />{k}} \right)^z }}<br />{{1 + \frac{z}<br />{k}}}} = \frac{{e^{ - \gamma z} }}<br />{z}\prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{z}<br />{k}} \right)^{ - 1} e^{\frac{z}<br />{k}} } <br />$$$ ver acá http://en.wikipedia.org/wiki/Gamma_function 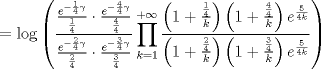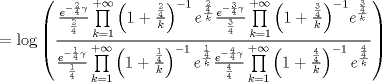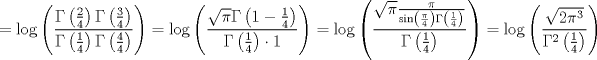$TEX: $$<br /> = \log \left( {\frac{{\frac{{e^{ - \frac{1}<br />{4}\gamma } }}<br />{{\frac{1}<br />{4}}} \cdot \frac{{e^{ - \frac{4}<br />{4}\gamma } }}<br />{{\frac{4}<br />{4}}}}}<br />{{\frac{{e^{ - \frac{2}<br />{4}\gamma } }}<br />{{\frac{2}<br />{4}}} \cdot \frac{{e^{ - \frac{3}<br />{4}\gamma } }}<br />{{\frac{3}<br />{4}}}}}\prod\limits_{k = 1}^{ + \infty } {\frac{{\left( {1 + \frac{{\frac{1}<br />{4}}}<br />{k}} \right)\left( {1 + \frac{{\frac{4}<br />{4}}}<br />{k}} \right)e^{\frac{5}<br />{{4k}}} }}<br />{{\left( {1 + \frac{{\frac{2}<br />{4}}}<br />{k}} \right)\left( {1 + \frac{{\frac{3}<br />{4}}}<br />{k}} \right)e^{\frac{5}<br />{{4k}}} }}} } \right)<br />$$$ $TEX: $$<br /> = \log \left( {\frac{{\frac{{e^{ - \frac{2}<br />{4}\gamma } }}<br />{{\frac{2}<br />{4}}}\prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{{\frac{2}<br />{4}}}<br />{k}} \right)^{ - 1} e^{\frac{{\frac{2}<br />{4}}}<br />{k}} \frac{{e^{ - \frac{3}<br />{4}\gamma } }}<br />{{\frac{3}<br />{4}}}\prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{{\frac{3}<br />{4}}}<br />{k}} \right)} ^{ - 1} e^{\frac{{\frac{3}<br />{4}}}<br />{k}} } }}<br />{{\frac{{e^{ - \frac{1}<br />{4}\gamma } }}<br />{{\frac{1}<br />{4}}}\prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{{\frac{1}<br />{4}}}<br />{k}} \right)^{ - 1} e^{\frac{{\frac{1}<br />{4}}}<br />{k}} \frac{{e^{ - \frac{4}<br />{4}\gamma } }}<br />{{\frac{4}<br />{4}}}\prod\limits_{k = 1}^{ + \infty } {\left( {1 + \frac{{\frac{4}<br />{4}}}<br />{k}} \right)^{ - 1} e^{\frac{{\frac{4}<br />{4}}}<br />{k}} } } }}} \right)<br />$$$ $TEX: $$<br /> = \log \left( {\frac{{\Gamma \left( {\frac{2}<br />{4}} \right)\Gamma \left( {\frac{3}<br />{4}} \right)}}<br />{{\Gamma \left( {\frac{1}<br />{4}} \right)\Gamma \left( {\frac{4}<br />{4}} \right)}}} \right) = \log \left( {\frac{{\sqrt \pi \Gamma \left( {1 - \frac{1}<br />{4}} \right)}}<br />{{\Gamma \left( {\frac{1}<br />{4}} \right) \cdot 1}}} \right) = \log \left( {\frac{{\sqrt \pi \frac{\pi }<br />{{\sin \left( {\frac{\pi }<br />{4}} \right)\Gamma \left( {\frac{1}<br />{4}} \right)}}}}<br />{{\Gamma \left( {\frac{1}<br />{4}} \right)}}} \right) = \log \left( {\frac{{\sqrt {2\pi ^3 } }}<br />{{\Gamma ^2 \left( {\frac{1}<br />{4}} \right)}}} \right)<br />$$$ Mensaje modificado por master_c el Mar 29 2013, 05:18 PM

master_c	Apr 20 2013, 05:38 PM Publicado: #6
Invitado	el 2/3 debio ir fuera de la productoria, que lastima que nadie se motive a nada. Mensaje modificado por master_c el Apr 20 2013, 06:06 PM

« Posterior · Series · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 12:53 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.