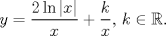 Todas las Peps de Calculo Aplicado, Ingenieria en Ejecución Año 2007 |
|
|
|
|
|
|
Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Santiago de Chile > Cálculo  |
 Jan 19 2008, 04:52 PM
Publicado:
#1
|
|
 Dios Matemático  Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad:  Colegio/Liceo:  Sexo:   |
Lo Prometido es Deuda asi que Aqui van Todas las PEPS de Calculo Aplicado del 2007
PEP 1 Calculo Aplicado Fecha: 24/04/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabccacaqGHbGaaeykaiaabccacaqGqbGaaeOCaiaabwha<br />% caqGLbGaaeOyaiaabwgacaqGGaGaaeyCaiaabwhacaqGLbGaaeOoai<br />% aabccacqGHaiIicaWGHbGaaiilaiaadkgacqGHiiIZcqWIDesOdaah<br />% aaWcbeqaaiabgUcaRaaakiabgkDiEpaakaaabaGaamyyaiabgUcaRi<br />% aadkgaaSqabaGccqGHKjYOdaGcaaqaaiaadggaaSqabaGccqGHRaWk<br />% daGcaaqaaiaadkgaaSqabaaakeaacaqGdbGaae4Baiaab6gacaqGGa<br />% GaaeyzaiaabYgacaqGSbGaae4BaiaabccacaqGWbGaaeOCaiaabwha<br />% caqGLbGaaeOyaiaabwgacaqGGaGaaeyCaiaabwhacaqGLbGaaeOoai<br />% abgcGiIiaadggacaGGSaGaamOyaiaacYcacaWGJbGaeyicI4SaeSyh<br />% He6aaWbaaSqabeaacqGHRaWkaaGccqGHshI3daGcaaqaaiaadggacq<br />% GHRaWkcaWGIbGaey4kaSIaam4yaaWcbeaakiabgsMiJoaakaaabaGa<br />% amyyaaWcbeaakiabgUcaRmaakaaabaGaamOyaaWcbeaakiabgUcaRm<br />% aakaaabaGaam4yaaWcbeaaaOqaaiaadkgacaGGPaGaaeOuaiaabwga<br />% caqGZbGaaeyDaiaabwgacaqGSbGaaeODaiaabggacaqGGaGaaeiBai<br />% aabggacaqGGaGaaeyAaiaab6gacaqGLbGaae4yaiaabwhacaqGHbGa<br />% ae4yaiaabMgacaqGZdGaaeOBaiaabQdadaGcaaqaaiaadIhadaahaa<br />% WcbeqaaiaaikdaaaGccqGHsislcaaIZaaaleqaaOGaey4kaSYaaqWa<br />% aeaacaWG4baacaGLhWUaayjcSdGaeyipaWJaaG4maiaac6caaeaaca<br />% qGtbGaaeyzaiaabgpacaqGHbGaaeiBaiaabwgacaqGGaGaae4Caiaa<br />% bwhacaqGWbGaaeOCaiaabwgacaqGTbGaae4BaiaabccacaqGLbGaae<br />% iiaiaabMgacaqGUbGaaeOzaiaabMgacaqGTbGaae4BaiaabYcacaqG<br />% GaGaae4CaiaabMgacaqGGaGaaeyzaiaabohacaqGGaGaaeyCaiaabw<br />% hacaqGLbGaaeiiaiaabYgacaqGVbGaae4CaiaabccacaqG0bGaaeyA<br />% aiaabwgacaqGUbGaaeyzaiaab6caaeaacaqGYaGaaeOlaiaabggaca<br />% qGPaGaaeiiaiaabofacaqGPbGaaeOoaiaabccacaqGdbGaae4Baiaa<br />% bshacaqGNbGaeqiUdeNaaeypamaalaaabaGaae4maaqaaiaabkdaaa<br />% GaaeiiaiaabweacaqGUbGaae4yaiaabwhacaqGLbGaaeOBaiaabsha<br />% caqGYbGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaqG2bGaaeyyai<br />% aabYgacaqGVbGaaeOCaiaabccacaqGKbGaaeyzaiaabccadaWcaaqa<br />% aiaabodacaqGZbGaaeyzaiaab6gacqaH4oqCcaqGGaGaaeylaiaabc<br />% cacaqGYaGaae4yaiaab+gacaqGZbGaeqiUdehabaGaaG4maiaadoha<br />% caWGLbGaamOBaiabgUcaRiaaikdaciGGJbGaai4BaiaacohacqaH4o<br />% qCaaaabaGaamOyaiaacMcacaqGebGaaeyzaiaabohacaqGKbGaaeyz<br />% aiaabccacaqG1bGaaeOBaiaabccacaqGMbGaaeyyaiaabkhacaqGVb<br />% GaaeiiaiaabsgacaqGLbGaaeiiaiaabkdacaqGWaGaaeiiaiaab2ga<br />% caqG0bGaae4Caiaab6cacaqGGaGaaeizaiaabwgacaqGGaGaaeyyai<br />% aabYgacaqG0bGaae4BaiaabccacaqGZbGaaeyzaiaabccacaqGVbGa<br />% aeOyaiaabohacaqGLbGaaeOCaiaabAhacaqGHbGaaeOBaiaabccaca<br />% qGKbGaae4BaiaabohacaqGGaGaaeOyaiaab+gacaqG0bGaaeyzaiaa<br />% bohacaqGGaGaaeiAaiaabggacaqGJbGaaeyAaiaabggacaqGGaGaae<br />% yzaiaabYgacaqGGaGaae4BaiaabwgacaqGZbGaaeiDaiaabwgacaqG<br />% GaaabaGaae4CaiaabwgacaqGNbGaaeO+aiaab6gacaqGGaGaaeiBai<br />% aab+gacaqGZbGaaeiiaiaabgoacaqGUbGaae4zaiaabwhacaqGSbGa<br />% ae4BaiaabohacaqGGaGaaeizaiaabwgacaqGGaGaaeizaiaabwgaca<br />% qGWbGaaeOCaiaabwgacaqGZbGaaeyAaiaabopacaqGUbGaaeiiaiaa<br />% bsgacaqGLbGaaeiiaiaabsdacaqG1aGaeyiSaaRaaeiiaiaabMhaca<br />% qGGaGaaeOnaiaabcdacqGHWcaScaqGGaGaaeOCaiaabwgacaqGZbGa<br />% aeiCaiaabwgacaqGJbGaaeiDaiaabMgacaqG2bGaaeyyaiaab2gaca<br />% qGLbGaaeOBaiaabshacaqGLbGaaeOlaiaabccacaqGibGaaeyyaiaa<br />% bYgacaqGSbGaaeyyaiaabkhacaqGGaGaaeiBaiaabggacaqGGaaaba<br />% GaaeizaiaabMgacaqGZbGaaeiDaiaabggacaqGUbGaae4yaiaabMga<br />% caqGHbGaaeiiaiaabwgacaqGUbGaaeiDaiaabkhacaqGLbGaaeiiai<br />% aabwgacaqGSbGaaeiBaiaab+gacaqGZbGaaeOlaaqaaiaabodacaqG<br />% UaGaaeiraiaabwgacaqG0bGaaeyzaiaabkhacaqGTbGaaeyAaiaab6<br />% gacaqGLbGaaeiiaiaabohacaqGPbGaaeiiaiaabYgacaqGHbGaaeii<br />% aiaabwgacaqG4bGaaeiCaiaabkhacaqGLbGaae4CaiaabMgacaqGZd<br />% GaaeOBaiaabccaaeaacaWG4bGaey4kaSYaaSaaaeaacaaIXaaabaGa<br />% amyEaiabgkHiTiaaiodaaaGaeyypa0JaaG4naaqaaiaabseacaqGLb<br />% Gaae4CaiaabogacaqGYbGaaeyAaiaabkgacaqGLbGaaeiiaiaabwha<br />% caqGUbGaaeyyaiaabccacaqGMbGaaeyDaiaab6gacaqGJbGaaeyAai<br />% aabopacaqGUbGaaeOlaiaabEeacaqGYbGaaeyyaiaabAgacaqGPbGa<br />% aeyCaiaabwhacaqGLbaabaGaaeinaiaab6cacaqGGaGaaeiraiaabw<br />% gacaqGTbGaaeyDaiaabwgacaqGZbGaaeiDaiaabkhacaqGLbGaaeii<br />% aiaabghacaqG1bGaaeyzaiaabQdaaeaacaqGHbGaaeykaiabgcGiIi<br />% aadIhacqGHiiIZcqWIDesOcqGHshI3caWG4bGaeS4JPFMaaGimaiab<br />% g2da9iaaicdaaeaacaqGIbGaaeykaiabgcGiIiaadIhacqGHiiIZcq<br />% WIDesOcqGHshI3caGGOaGaeyOeI0IaaGymaiaacMcacqWIpM+zcaWG<br />% 4bGaeyypa0JaeyOeI0IaamiEaaqaaiaaiwdacaGGUaGaaeiraiaabg<br />% gacaqGKbGaaeyyaiaabccacaqGSbGaaeyyaiaabohacaqGGaGaaeOr<br />% aiaabwhacaqGUbGaae4yaiaabMgacaqGVbGaaeOBaiaabwgacaqGZb<br />% GaaeOoaaqaaiaadAgacaGGOaGaamiEaiaacMcacqGH9aqpdaWcaaqa<br />% aiaaikdacaWG4baabaGaamiEaiabgkHiTiaaigdaaaGaai4oaiaadE<br />% gacaGGOaGaamiEaiaacMcacqGH9aqpdaWcaaqaaiaadIhacqGHRaWk<br />% caaIYaaabaGaamiEaiabgUcaRiaaigdaaaaabaGaaeyyaiaabMcaca<br />% qGGaGaaeyzaiaab6gacaqGJbGaaeyDaiaabwgacaqGUbGaaeiDaiaa<br />% bkhacaqGLbGaaeiiaiaabseacaqGVbGaaeyBaiaabMgacaqGUbGaae<br />% yAaiaab+gacaqGZbGaaeiiaiaabMhacaqGGaGaaeOCaiaabwgacaqG<br />% JbGaae4BaiaabkhacaqGYbGaaeyAaiaabsgacaqGVbGaae4Caiaabc<br />% cacaqGKbGaaeyzaiaabccacaqGHbGaaeyBaiaabkgacaqGHbGaae4C<br />% aaqaaiaabkgacaqGPaGaaeiiaiaaboeacaqGHbGaaeiBaiaabogaca<br />% qG1bGaaeiBaiaabwgacaqGGaGaaiikaiaadAgacqWIyiYBcaWGNbWa<br />% aWbaaSqabeaacqGHsislcaaIXaaaaOGaaiykaiaacIcacaWG4bGaey<br />% 4kaSIaaGymaiaacMcacaGGUaaaaaa!5982!<br />\[<br />\begin{gathered}<br /> 1.{\text{ a) Pruebe que: }}\forall a,b \in \mathbb{R}^ + \Rightarrow \sqrt {a + b} \leqslant \sqrt a + \sqrt b \hfill \\<br /> {\text{Con ello pruebe que:}}\forall a,b,c \in \mathbb{R}^ + \Rightarrow \sqrt {a + b + c} \leqslant \sqrt a + \sqrt b + \sqrt c \hfill \\<br /> b){\text{Resuelva la inecuaci\'o n:}}\sqrt {x^2 - 3} + \left| x \right| < 3. \hfill \\<br /> {\text{Se\~n ale supremo e infimo}}{\text{, si es que los tiene}}{\text{.}} \hfill \\<br /> {\text{2}}{\text{.a) Si: Cotg}}\theta {\text{ = }}\frac{{\text{3}}}<br />{{\text{2}}}{\text{ Encuentre el valor de }}\frac{{{\text{3sen}}\theta {\text{ - 2cos}}\theta }}<br />{{3sen + 2\cos \theta }} \hfill \\<br /> b){\text{Desde un faro de 20 mts}}{\text{. de alto se observan dos botes hacia el oeste }} \hfill \\<br /> {\text{seg\'u n los \'a ngulos de depresi\'o n de 45}}^\circ {\text{ y 60}}^\circ {\text{ respectivamente}}{\text{. Hallar la }} \hfill \\<br /> {\text{distancia entre ellos}}{\text{.}} \hfill \\<br /> {\text{3}}{\text{.Determine si la expresi\'o n }} \hfill \\<br /> x + \frac{1}<br />{{y - 3}} = 7 \hfill \\<br /> {\text{Describe una funci\'o n}}{\text{.Grafique}} \hfill \\<br /> {\text{4}}{\text{. Demuestre que:}} \hfill \\<br /> {\text{a)}}\forall x \in \mathbb{R} \Rightarrow x0 = 0 \hfill \\<br /> {\text{b)}}\forall x \in \mathbb{R} \Rightarrow ( - 1)x = - x \hfill \\<br /> 5.{\text{Dada las Funciones:}} \hfill \\<br /> f(x) = \frac{{2x}}<br />{{x - 1}};g(x) = \frac{{x + 2}}<br />{{x + 1}} \hfill \\<br /> {\text{a) encuentre Dominios y recorridos de ambas}} \hfill \\<br /> {\text{b) Calcule }}(f \circ g^{ - 1} )(x + 1). \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/a3c47430c67175eacc119bf3642b746c.png) Por favor no posteen aún, esperen a que termine, miren que son hartas ^^ Saludos DavE -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial      |
 |
 
|
|
Jan 19 2008, 05:12 PM
Publicado:
#2
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
PEP 2 Calculo Aplicado
Fecha: 05/06/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabccacaqGbbGaaeiCaiaabYgacaqGPbGaae4yaiaabgga<br />% caqGUbGaaeizaiaab+gacaqGGaGaaeiBaiaabggacaqGGaGaaeizai<br />% aabwgacaqGMbGaaeyAaiaab6gacaqGPbGaae4yaiaabMgacaqGZdGa<br />% aeOBaiaabccacaqGKbGaaeyzaiaabccacaqGebGaaeyzaiaabkhaca<br />% qGPbGaaeODaiaabggacaqGKbGaaeyyaiaabUdacaqGGaGaae4qaiaa<br />% bggacaqGSbGaae4yaiaabwhacaqGSbGaaeyzaiaabccaceWG5bGbau<br />% aacaGGOaGaamiEaiaacMcacaqGGaGaae4CaiaabMgacaqGGaGaamyE<br />% aiaacIcacaWG4bGaaiykaiabg2da9iaaikdaciGGJbGaai4Baiaaco<br />% hacaGGOaGaaGOmaiaadIhacaGGPaaabaaabaGaaGOmaiaac6cacaqG<br />% GaGaaeiuaiaabkhacaqG1bGaaeyzaiaabkgacaqGLbGaaeiiaiaabg<br />% hacaqG1bGaaeyzaiaabccacaqGSbGaaeyyaiaabccacaqGLbGaae4y<br />% aiaabwhacaqGHbGaae4yaiaabMgacaqGZdGaaeOBaiaabQdaaeaaca<br />% aIXaGaeyOeI0IaamiEamaaCaaaleqabaGaaGOmaaaakiaacIcaceWG<br />% 5bGbauaacaGGPaGaeyOeI0IaamiEaiaadMhacqGHRaWkcaaIXaGaey<br />% ypa0JaaGimaiaacYcacaqGGaGaae4CaiaabwgacaqGGaGaae4qaiaa<br />% bwhacaqGTbGaaeiCaiaabYgacaqGLbGaaeiiaiaabshacaqGHbGaae<br />% OBaiaabshacaqGVbGaaeiiaiaabchacaqGHbGaaeOCaiaabggacaqG<br />% GaaabaGaamyEaiabg2da9maalaaabaGaciiBaiaac6gacaGGOaGaam<br />% iEaiabgUcaRmaakaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiab<br />% gkHiTiaaigdaaSqabaGccaGGPaaabaWaaOaaaeaacaWG4bWaaWbaaS<br />% qabeaacaaIYaaaaOGaeyOeI0IaaGymaaWcbeaaaaGccaGGSaGaaeii<br />% aiaabogacaqGVbGaaeyBaiaab+gacaqGGaGaaeiDaiaabggacaqGTb<br />% GaaeOyaiaabMgacaqGPdGaaeOBaiaabccacaqGWbGaaeyyaiaabkha<br />% caqGHbGaaeOoaiaabccacaWG5bGaeyypa0ZaaSaaaeaacaWGbbGaam<br />% OCaiaadogaciGGJbGaai4BaiaacohacaGGOaGaamiEaiaacMcaaeaa<br />% daGcaaqaaiaaigdacqGHsislcaWG4bWaaWbaaSqabeaacaaIYaaaaa<br />% qabaaaaOGaaiOlaaqaaaqaaiaaiodacaGGUaGaaeiiaiaabofacaqG<br />% PbGaaeOoaiaadAgacaGGOaGaamyDaiaacMcacqGH9aqpdaWcaaqaai<br />% aaigdaaeaacaWG1bWaaWbaaSqabeaacaaIYaaaaaaakiaacUdacaWG<br />% NbGaaiikaiaadIhacaGGPaGaeyypa0ZaaSaaaeaadaGcaaqaaiaadI<br />% haaSqabaaakeaadaGcaaqaaiaaikdacaWG4bWaaWbaaSqabeaacaaI<br />% YaaaaOGaeyOeI0IaaGOnaiaadIhacqGHRaWkcaaIXaaaleqaaaaaki<br />% aacUdacaqGdbGaaeyyaiaabYgacaqGJbGaaeyDaiaabYgacaqGLbGa<br />% aeiiaiaabYgacaqGHbGaaeiiaiaabsgacaqGLbGaaeOCaiaabMgaca<br />% qG2bGaaeyyaiaabsgacaqGHbGaaeiiaiaabsgacaqGLbGaaeiiaiaa<br />% cIcacaWGMbGaeSigI8Maam4zaiaacMcacaGGOaGaamiEaiaacMcaae<br />% aacaqGKbGaaeyzaiaabccacaqGKbGaae4BaiaabohacaqGGaGaaeyB<br />% aiaabggacaqGUbGaaeyzaiaabkhacaqGHbGaae4CaiaabQdacaqGGa<br />% GaaeyyaiaabMcacaqGGaGaaeyraiaab6gacaqGJbGaae4Baiaab6ga<br />% caqG0bGaaeOCaiaabggacaqGUbGaaeizaiaab+gacaGGOaGaamOzai<br />% ablIHiVjaadEgacaGGPaGaaiikaiaadIhacaGGPaaabaGaaeOyaiaa<br />% bMcacaqGvbGaae4CaiaabggacaqGUbGaaeizaiaab+gacaqGGaGaae<br />% OCaiaabwgacaqGNbGaaeiBaiaabggacaqGGaGaaeizaiaabwgacaqG<br />% GaGaaeiBaiaabggacaqGGaGaae4yaiaabggacaqGKbGaaeyzaiaab6<br />% gacaqGHbGaaeiiaiaabchacaqGHbGaaeOCaiaabggacaqGGaGaaeiz<br />% aiaabwgacaqGYbGaaeyAaiaabAhacaqGHbGaaeOCaiaabccacaWGMb<br />% GaaiikaiaadEgacaGGOaGaamiEaiaacMcacaGGPaGaaiOlaaqaaaqa<br />% aiaaisdacaGGUaGaaeiiaiaabofacaqGPbGaaeiiaiaadAgacaGGOa<br />% GaamiEaiaacMcacqGH9aqpcaaIYaGaci4yaiaac+gacaGGZbGaaGOm<br />% aiaadIhacaGGUaGaaeiiaiaaboeacaqGHbGaaeiBaiaabogacaqG1b<br />% GaaeiBaiaabwgacaqGGaGaamyEamaaCaaaleqabaGaaiikaiaad6ga<br />% caGGPaaaaOGaaiikaiaadIhacaGGPaaabaaabaGaaGynaiaac6caca<br />% qGebGaaeyyaiaabsgacaqGHbGaaeiiaiaabYgacaqGHbGaaeiiaiaa<br />% boeacaqG1bGaaeOCaiaabAhacaqGHbGaaeOoaiaabccadaWcaaqaai<br />% aadIhadaahaaWcbeqaaiaaikdaaaaakeaacaWGHbWaaWbaaSqabeaa<br />% caaIYaaaaaaakiabgUcaRmaalaaabaGaamyEamaaCaaaleqabaGaaG<br />% OmaaaaaOqaaiaadkgadaahaaWcbeqaaiaaikdaaaaaaOGaeyypa0Ja<br />% aGymaiaac6cacaqGGaGaaeiuaiaabkhacaqG1bGaaeyzaiaabkgaca<br />% qGLbGaaeiiaiaabghacaqG1bGaaeyzaiaabccacaqGSbGaaeyyaiaa<br />% bccacaqGYbGaaeyzaiaabogacaqG0bGaaeyyaiaabccacaqG0bGaae<br />% yyaiaab6gacaqGNbGaaeyzaiaab6gacaqG0bGaaeyzaiaabccacaqG<br />% LbGaaeOBaiaabccacaqG1bGaaeOBaaqaaiaabchacaqG1bGaaeOBai<br />% aabshacaqGVbGaaeiiaiaadcfadaWgaaWcbaGaaGimaaqabaGccaGG<br />% OaGaamiEamaaBaaaleaacaaIWaaabeaakiaacYcacaWG5bWaaSbaaS<br />% qaaiaaicdaaeqaaOGaaiykaiaabccacaqGubGaae4Baiaab2gacaqG<br />% HbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqGVbGaaeOCaiaab2<br />% gacaqGHbGaaeOoaiaadIhacaWG4bWaaSbaaSqaaiaaicdaaeqaaOGa<br />% ey4kaSIaamyEaiaadMhadaWgaaWcbaGaaGimaaqabaGccqGH9aqpca<br />% aIXaaabaGaaeisaiaabMgacaqGUbGaaeiDaiaabQdacaqGGaGaae4u<br />% aiaabwgacaqGGaGaaeyqaiaabsgacaqG2bGaaeyAaiaabwgacaqGYb<br />% GaaeiDaiaabwgacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiaiaabIga<br />% caqGHbGaaeyEaiaabccacaqGKbGaaeyzaiaabkhacaqGPbGaaeODai<br />% aabggacaqGKbGaaeyyaiaabccacaqGjbGaaeyBaiaabchacaqGSbGa<br />% aeyAaiaabogacaqGPbGaaeiDaiaabggaaaaa!F1BA!<br />\[<br />\begin{gathered}<br /> 1.{\text{ Aplicando la definici\'o n de Derivada; Calcule }}y'(x){\text{ si }}y(x) = 2\cos (2x) \hfill \\<br /> \hfill \\<br /> 2.{\text{ Pruebe que la ecuaci\'o n:}} \hfill \\<br /> (1 - x^2)(y') - xy + 1 = 0,{\text{ se Cumple tanto para }} \hfill \\<br /> y = \frac{{\ln (x + \sqrt {x^2 - 1} )}}<br />{{\sqrt {x^2 - 1} }},{\text{ como tambi\'e n para: }}y = \frac{{Arc\cos (x)}}<br />{{\sqrt {1 - x^2 } }}. \hfill \\<br /> \hfill \\<br /> 3.{\text{ Si:}}f(u) = \frac{1}<br />{{u^2 }};g(x) = \frac{{\sqrt x }}<br />{{\sqrt {2x^2 - 6x + 1} }};{\text{Calcule la derivada de }}(f \circ g)(x) \hfill \\<br /> {\text{de dos maneras: a) Encontrando}}(f \circ g)(x) \hfill \\<br /> {\text{b)Usando regla de la cadena para derivar }}f(g(x)). \hfill \\<br /> \hfill \\<br /> 4.{\text{ Si }}f(x) = 2\cos 2x.{\text{ Calcule }}y^{(n)} (x) \hfill \\<br /> \hfill \\<br /> 5.{\text{Dada la Curva: }}\frac{{x^2 }}<br />{{a^2 }} + \frac{{y^2 }}<br />{{b^2 }} = 1.{\text{ Pruebe que la recta tangente en un}} \hfill \\<br /> {\text{punto }}P_0 (x_0 ,y_0 ){\text{ Toma la forma:}}xx_0 + yy_0 = 1 \hfill \\<br /> {\text{Hint: Se Advierte que hay derivada Implicita}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/c8a1ad915a16300d3b188ad19b2093c4.png)
Mensaje modificado por davosalinas el Jan 21 2008, 06:01 PM -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 05:38 PM
Publicado:
#3
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
PAS(Prueba Acumulativa Semestral) Calculo Aplicado
Fecha: 10/07/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabccacaqGebGaaeyzaiaabsgacaqG1bGaae4yaiaabMga<br />% caqGYbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqGVbGaaeOCai<br />% aab2gacaqG1bGaaeiBaiaabggacaqGGaGaaeizaiaabwgacaqGGaGa<br />% aeOCaiaabwgacaqGJbGaaeyDaiaabkhacaqGYbGaaeyzaiaab6gaca<br />% qGJbGaaeyAaiaabggacaqG6aaabaGaaeysamaaBaaaleaacaWGUbaa<br />% beaakiabg2da9iaad6gacaWG4bWaaWbaaSqabeaacaWGUbGaeyOeI0<br />% IaaGymaaaakiGacogacaGGVbGaai4CaiaadIhacqGHRaWkcaWG4bWa<br />% aWbaaSqabeaacaWGUbaaaOGaam4CaiaadwgacaWGUbGaamiEaiabgk<br />% HiTiaad6gacaGGOaGaamOBaiabgkHiTiaaigdacaGGPaGaaeysamaa<br />% BaaaleaacaWGUbGaeyOeI0IaaGOmaaqabaaakeaacaqGqbGaaeyyai<br />% aabkhacaqGHbGaaeiiaiaabYgacaqGHbGaaeiiaiaabMeacaqGUbGa<br />% aeiDaiaabwgacaqGNbGaaeOCaiaabggacaqGSbGaaeiiaiaabQdaca<br />% qGGaGaaeysamaaBaaaleaacaWGUbaabeaakiabg2da9maapeaabaGa<br />% amiEamaaCaaaleqabaGaamOBaaaakiGacogacaGGVbGaai4CaiaadI<br />% hacaWGKbGaamiEaiaac6caaSqabeqaniabgUIiYdGccaqGGaaabaGa<br />% ae4qaiaab+gacaqGUbGaaeiiaiaabwgacaqGSbGaaeiBaiaab+gaca<br />% qGGaGaae4yaiaabggacaqGSbGaae4yaiaabwhacaqGSbGaaeyzaiaa<br />% bQdacaqGGaWaa8qaaeaacaWG4bWaaWbaaSqabeaacaaIZaaaaOGaci<br />% 4yaiaac+gacaGGZbGaamiEaiaadsgacaWG4baaleqabeqdcqGHRiI8<br />% aaGcbaGaaeisaiaabMgacaqGUbGaaeiDaiaabQdacaqGGaGaaeytai<br />% aabwgacaqG0bGaae4BaiaabsgacaqGVbGaaeiiaiaabsgacaqGLbGa<br />% aeiiaiaabMgacaqGUbGaaeiDaiaabwgacaqGNbGaaeOCaiaabggaca<br />% qGJbGaaeyAaiaabopacaqGUbGaaeiiaiaabchacaqGVbGaaeOCaiaa<br />% bccacaqGWbGaaeyyaiaabkhacaqG0bGaaeyzaiaabohaaeaaaeaaca<br />% qGYaGaaeOlaiaabseacaqGLbGaaeyBaiaab+gacaqGZbGaaeiDaiaa<br />% bkhacaqGHbGaaeOCaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaae<br />% iBaiaabggacaqGZbGaaeiiaiaabkhacaqGLbGaae4yaiaabshacaqG<br />% HbGaae4CaiaabccacaqG0bGaaeyyaiaab6gacaqGNbGaaeyzaiaab6<br />% gacaqG0bGaaeyzaiaabohacaqGGaGaaeyyaiaabccacaqGSbGaaeyy<br />% aiaabccacaqGObGaaeyAaiaabchacaqGLbGaaeOCaiaabkgacaqGVb<br />% GaaeiBaiaabggacaqG6aGaaeiiaiaadMhacaGGOaGaamiEaiabgkHi<br />% TiaaikdacaGGPaGaeyypa0JaamiEaiabgkHiTiaaisdacaGGSaaaba<br />% Gaaeyzaiaab6gacaqGGaGaaeiBaiaab+gacaqGZbGaaeiiaiaabcha<br />% caqG1bGaaeOBaiaabshacaqGVbGaae4CaiaabccacaqGKbGaaeyzai<br />% aabccacaqGPbGaaeOBaiaabshacaqGLbGaaeOCaiaabohacaqGLbGa<br />% ae4yaiaabogacaqGPbGaae48aiaab6gacaqGGaGaaeizaiaabwgaca<br />% qGGaGaaey6aiaabohacaqG0bGaaeyyaiaabccacaqG5bGaaeiiaiaa<br />% bYgacaqGVbGaae4CaiaabccacaqGLbGaaeOAaiaabwgacaqGZbGaae<br />% iiaiaabogacaqGVbGaae4BaiaabkhacaqGKbGaaeyzaiaab6gacaqG<br />% HbGaaeizaiaab+gacaqGZbGaaeiiaiaabohacaqGVbGaaeOBaiaabc<br />% cacaqGWbGaaeyyaiaabkhacaqGHbGaaeiBaiaabwgacaqGSbGaaeyy<br />% aiaabohaaaaa!452F!<br />\[<br />\begin{gathered}<br /> 1.{\text{ Deducir la formula de recurrencia:}} \hfill \\<br /> {\text{I}}_n = nx^{n - 1} \cos x + x^n senx - n(n - 1){\text{I}}_{n - 2} \hfill \\<br /> {\text{Para la Integral : I}}_n = \int {x^n \cos xdx.} {\text{ }} \hfill \\<br /> {\text{Con ello calcule: }}\int {x^3 \cos xdx} \hfill \\<br /> {\text{Hint: Metodo de integraci\'o n por partes}} \hfill \\<br /> \hfill \\<br /> {\text{2}}{\text{.Demostrar que las rectas tangentes a la hiperbola: }}y(x - 2) = x - 4, \hfill \\<br /> {\text{en los puntos de intersecci\'o n de \'e sta y los ejes coordenados son paralelas}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/2a2760eb2ee2f2f92f795ffaa02226e8.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGZa<br />% GaaeOlaiaabcfacaqGYbGaaeyDaiaabwgacaqGIbGaaeyzaiaabcca<br />% caqGXbGaaeyDaiaabwgacaqGGaGaamyEaiaacIcacaWG4bGaaiykai<br />% abg2da9iaadoeadaWgaaWcbaGaaGymaaqabaGccaWGLbWaaWbaaSqa<br />% beaacqGHsislcaWG4baaaOGaci4yaiaac+gacaGGZbGaaGOmaiaadI<br />% hacqGHRaWkcaWGdbWaaSbaaSqaaiaaikdaaeqaaOGaamyzamaaCaaa<br />% leqabaGaeyOeI0IaamiEaaaakiaadohacaWGLbGaamOBaiaaikdaca<br />% WG4bGaai4oaiaadoeadaWgaaWcbaGaaGymaaqabaGccaGGSaGaam4q<br />% amaaBaaaleaacaaIYaaabeaakiaabccacaqGJbGaae4Baiaab6gaca<br />% qGZbGaaeiDaiaabggacaqGUbGaaeiDaiaabwgacaqGZbGaae4oaiaa<br />% bccacaqGZbGaaeyyaiaabshacaqGPbGaae4CaiaabAgacaqGHbGaae<br />% 4yaiaabwgacaqGUbGaaeiiaiaabYgacaqGHbaabaGaaeyzaiaaboga<br />% caqG1bGaaeyyaiaabogacaqGPbGaae48aiaab6gacaqG6aaabaGabm<br />% yEayaafyaafaGaaiikaiaadIhacaGGPaGaey4kaSIaaGOmaiqadMha<br />% gaqbaiaacIcacaWG4bGaaiykaiabgUcaRiaaiwdacaWG5bGaaiikai<br />% aadIhacaGGPaGaeyypa0JaaGimaaaaaa!8C83!<br />\[<br />\begin{gathered}<br /> {\text{3}}{\text{.Pruebe que }}y(x) = C_1 e^{ - x} \cos 2x + C_2 e^{ - x} sen2x;C_1 ,C_2 {\text{ constantes; satisfacen la}} \hfill \\<br /> {\text{ecuaci\'o n:}} \hfill \\<br /> y''(x) + 2y'(x) + 5y(x) = 0 \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/07b1ad7de5ef307291476ab073fc9b86.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqG0a<br />% GaaeOlaiaabIeacaqGHbGaaeyEaiaabccacaqGXbGaaeyDaiaabwga<br />% caqGGaGaae4yaiaabwgacaqGYbGaae4yaiaabggacaqGYbGaaeiiai<br />% aabwhacaqGUbGaaeiiaiaabshacaqGLbGaaeOCaiaabkhacaqGLbGa<br />% aeOBaiaab+gacaqGGaGaaeOCaiaabwgacaqGJbGaaeiDaiaabggaca<br />% qGUbGaae4zaiaabwhacaqGSbGaaeyyaiaabkhacaqGGaGaae4yaiaa<br />% b+gacaqGUbGaaeiiaiaabgdacaqGWaGaaeimaiaabccacaqGTbGaae<br />% yzaiaabshacaqGYbGaae4BaiaabohacaqGGaGaaeizaiaabwgacaqG<br />% GaGaaeyBaiaabggacaqGSbGaaeiBaiaabggacaqGGaaabaGaae4Bai<br />% aabogacaqG1bGaaeiCaiaabggacaqGUbGaaeizaiaab+gacaqGGaGa<br />% aeiCaiaabggacaqGYbGaaeyyaiaabccacaqGLbGaaeiBaiaabYgaca<br />% qGVbGaaeiiaiaabwhacaqGUbGaaeyyaiaabccacaqGTbGaaeyDaiaa<br />% bkhacaqGHbGaaeiBaiaabYgacaqGHbGaaeiiaiaabohacaqG1bGaae<br />% OzaiaabMgacaqGJbGaaeyAaiaabwgacaqGUbGaaeiDaiaabwgacaqG<br />% TbGaaeyzaiaab6gacaqG0bGaaeyzaiaabccacaqGSbGaaeyyaiaabk<br />% hacaqGNbGaaeyyaiaab6caaeaacaqGdbGaaeyDaiaabgoacaqGSbGa<br />% aeyzaiaabohacaqGGaGaae4Caiaab+gacaqGUbGaaeiiaiaabYgaca<br />% qGHbGaae4CaiaabccacaqGKbGaaeyAaiaab2gacaqGLbGaaeOBaiaa<br />% bohacaqGPbGaae4Baiaab6gacaqGLbGaae4CaiaabccacaqGKbGaae<br />% yzaiaabccacaqGSbGaae4BaiaabohacaqGGaGaaeiDaiaabkhacaqG<br />% LbGaae4CaiaabccacaqGSbGaaeyyaiaabsgacaqGVbGaae4Caiaabc<br />% cacaqGWbGaaeyyaiaabkhacaqGHbGaaeiiaiaabghacaqG1bGaaeyz<br />% aiaabccacaqGLbGaaeiBaiaabccacaqGHdGaaeOCaiaabwgacaqGHb<br />% GaaeiiaaqaaiaabogacaqGLbGaaeOCaiaabogacaqGHbGaaeizaiaa<br />% bggacaqGGaGaae4CaiaabwgacaqGHbGaaeiiaiaab2gacaqGHbGaae<br />% iEaiaabMgacaqGTbGaaeyyaiaab+daaaaa!E3F8!<br />\[<br />\begin{gathered}<br /> {\text{4}}{\text{.Hay que cercar un terreno rectangular con 100 metros de malla }} \hfill \\<br /> {\text{ocupando para ello una muralla suficientemente larga}}{\text{.}} \hfill \\<br /> {\text{Cu\'a les son las dimensiones de los tres lados para que el \'a rea }} \hfill \\<br /> {\text{cercada sea maxima?}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/6737097cb04c6eab5e72463dbd86c538.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqG1a<br />% GaaeOlaiaabseacaqGLbGaaeiDaiaabwgacaqGYbGaaeyBaiaabMga<br />% caqGUbGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaqG2bGaaeyyai<br />% aabYgacaqGVbGaaeOCaiaabccacaqGWbGaaeyyaiaabkhacaqGHbGa<br />% aeiiaiaabgeacaqGGaGaaeizaiaabwgacaqGGaGaaeyBaiaab+gaca<br />% qGKbGaae4BaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeiBaiaa<br />% bggacaqGGaGaaeOzaiaabwhacaqGUbGaae4yaiaabMgacaqGZdGaae<br />% OBaiaabccacaWGMbGaaiikaiaadIhacaGGPaGaaiOoaaqaaiaabcca<br />% caWGMbGaaiikaiaadIhacaGGPaGaeyypa0ZaaSaaaeaacaWGHbGaam<br />% OCaiaadogacaWGZbGaamyzaiaad6gacaGGOaGaamiEaiaacMcaaeaa<br />% caWG4baaaiaacUdacaWG4bGaeyipaWJaaGimaaqaaiaadAgacaGGOa<br />% GaamiEaiaacMcacqGH9aqpcaqGGaGaaeiiaiaabccacaWGbbGaai4o<br />% aiaadIhacqGH9aqpcaaIWaaabaGaamOzaiaacIcacaWG4bGaaiykai<br />% abg2da9maalaaabaGaamyzamaaCaaaleqabaGaamiEaaaakiabgkHi<br />% TiaaigdaaeaacaWG4baaaiaacUdacaWG4baccaGae8Npa4JaaGimaa<br />% qaaiaabofacaqGLbGaaeyyaiaabccacaqGJbGaae4Baiaab6gacaqG<br />% 0bGaaeyAaiaab6gacaqG1bGaaeyyaiaabccacaqGLbGaaeOBaiaabc<br />% cacaqG4bGaaeypaiaabcdaaaaa!9EE8!<br />\[<br />\begin{gathered}<br /> {\text{5}}{\text{.Determine el valor para A de modo que la funci\'o n }}f(x): \hfill \\<br /> {\text{ }}f(x) = \frac{{arcsen(x)}}<br />{x};x < 0 \hfill \\<br /> f(x) = {\text{ }}A;x = 0 \hfill \\<br /> f(x) = \frac{{e^x - 1}}<br />{x};x > 0 \hfill \\<br /> {\text{Sea continua en x = 0}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/0cf1ea21e9813368698f7d34dad84181.png) Es la misma funcion en la 5. Una de las pruebas mas faciles, definitivo. -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 06:02 PM
Publicado:
#4
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
PEP 3 Calculo Aplicado
Fecha:04/09/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGXa<br />% GaaeOlaiaabgeacaqG0bGaaeyzaiaab6gacaqGKbGaaeyAaiaabwga<br />% caqGUbGaaeizaiaab+gacaqGZbGaaeyzaiaabccacaqGHbGaaeiiai<br />% aabYgacaqGHbGaaeiiaiaabsgacaqGLbGaaeOzaiaabMgacaqGUbGa<br />% aeyAaiaabogacaqGPbGaae48aiaab6gacaqGGaGaaeizaiaabwgaca<br />% qGGaGaaeyDaiaab6gacaqGHbGaaeiiaiaabMeacaqGUbGaaeiDaiaa<br />% bwgacaqGNbGaaeOCaiaabggacaqGSbGaaeiiaiaabseacaqGLbGaae<br />% OzaiaabMgacaqGUbGaaeyAaiaabsgacaqGHbGaaeiiaiaabMhacaqG<br />% GaGaaeyzaiaabYgacaqGGaGaaeiDaiaabwgacaqGVbGaaeOCaiaabw<br />% gacaqGTbGaaeyyaaqaaiaabAeacaqG1bGaaeOBaiaabsgacaqGHbGa<br />% aeyBaiaabwgacaqGUbGaaeiDaiaabggacaqGSbGaaeiiaiaabsgaca<br />% qGLbGaaeiBaiaabccacaqGJbGaaeyyaiaabYgacaqGJbGaaeyDaiaa<br />% bYgacaqGVbGaaeilaiaabccacaqGdbGaaeyyaiaabYgacaqGJbGaae<br />% yDaiaabYgacaqGLbGaaeOoaaqaaiaadggacaGGPaWaaCbeaeaaciGG<br />% SbGaaiyAaiaac2gaaSqaaiaad6gacqGHsgIRcqGHEisPaeqaaOWaaa<br />% bCaeaacaaIYaGaeqiWdaNaeqyTdu2aaSbaaSqaaiabeQ7aRbqabaGc<br />% caGGOaGaaGymaiabgUcaRiabew7aLnaaBaaaleaacqaH6oWAaeqaaO<br />% WaaWbaaSqabeaacaaIYaaaaOGaaiykaiabfs5aenaaBaaaleaacqaH<br />% 6oWAaeqaaOGaamiEaiaacYcacaqGGaGaamiEaiabgIGiopaadmaaba<br />% GaaGimaiaacYcacaaI0aaacaGLBbGaayzxaaaaleaacaWGRbGaeyyp<br />% a0JaaGymaaqaaiaad6gaa0GaeyyeIuoakiaac6caaeaacaWGIbGaai<br />% ykamaalaaabaGaamizaaqaaiaadsgacaWG4baaamaapedabaGaaiik<br />% aiaadshadaahaaWcbeqaaiaaiodaaaGccqGHRaWkcaaIXaGaaiykam<br />% aaCaaaleqabaGaaGymaiaaicdaaaGccaWGKbGaamiDaaWcbaGaaG4m<br />% aiaadIhaaeaacaWG4bWaaWbaaWqabeaacaaIZaaaaaqdcqGHRiI8aa<br />% GcbaGaam4yaiaacMcadaWdXbqaamaalaaabaGaamizaiaadIhaaeaa<br />% daGcaaqaaiaaisdacqGHsislcaWG4bWaaWbaaSqabeaacaaIYaaaaa<br />% qabaaaaaqaaiaaikdaaeaacaaIWaaaniabgUIiYdGccaGG7aGaaiik<br />% aiaabIeacaqGPbGaaeOBaiaabshacaqG6aGaaeysaiaab2gacaqGWb<br />% GaaeOCaiaab+gacaqGWbGaaeyAaiaabggacaqGPaaabaaabaGaaeOm<br />% aiaab6cacaqGhbGaaeOCaiaabggacaqGMbGaaeyAaiaabghacaqG1b<br />% GaaeyzaiaabccacaqG5bGaaeiiaiaabwgacaqG2bGaaeyyaiaabYga<br />% caqG1bGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaqGHbGaaeOCai<br />% aabwgacaqGHbGaaeiiaiaabMgacaqGUbGaaeiDaiaabwgacaqGYbGa<br />% aeyAaiaab+gacaqGYbGaaeiiaiaabggacaqGGaGaeqyWdiNaeyypa0<br />% JaaGymaiabgUcaRiaadohacaWGLbGaamOBaiabeI7aXjaabccacaqG<br />% 5bGaaeiiaiaabwgacaqG4bGaaeiDaiaabwgacaqGYbGaaeyAaiaab+<br />% gacaqGYbGaaeiiaiaabggacaqGGaGaeqyWdiNaeyypa0JaaG4maiaa<br />% dohacaWGLbGaamOBaiabeI7aXbaaaa!21E6!<br />\[<br />\begin{gathered}<br /> {\text{1}}{\text{.Atendiendose a la definici\'o n de una Integral Definida y el teorema}} \hfill \\<br /> {\text{Fundamental del calculo}}{\text{, Calcule:}} \hfill \\<br /> a)\mathop {\lim }\limits_{n \to \infty } \sum\limits_{k = 1}^n {2\pi \varepsilon _\kappa (1 + \varepsilon _\kappa ^2 )\Delta _\kappa x,{\text{ }}x \in \left[ {0,4} \right]} . \hfill \\<br /> b)\frac{d}<br />{{dx}}\int_{3x}^{x^3 } {(t^3 + 1)^{10} dt} \hfill \\<br /> c)\int\limits_2^0 {\frac{{dx}}<br />{{\sqrt {4 - x^2 } }}} ;({\text{Hint:Impropia)}} \hfill \\<br /> \hfill \\<br /> {\text{2}}{\text{.Grafique y evalue el area interior a }}\rho = 1 + sen\theta {\text{ y exterior a }}\rho = 3sen\theta \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/f43954c28e52b881fe1da184eefbb33b.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIZa<br />% GaaiOlaiaabseacaqGLbGaaeiDaiaabwgacaqGYbGaaeyBaiaabMga<br />% caqGUbGaaeyzaiaabccacaqGLbGaaeiBaiaabccacaqGwbGaae4Bai<br />% aabYgacaqG1bGaaeyBaiaabwgacaqGUbGaaeiiaiaabsgacaqGLbGa<br />% aeiBaiaabccacaqGJbGaaeyDaiaabwgacaqGYbGaaeiCaiaab+gaca<br />% qGGaGaaeizaiaabwgacaqGGaGaaeOCaiaab+gacaqG0bGaaeyyaiaa<br />% bogacaqGPbGaae48aiaab6gacaqGSaGaaeiiaiaabogacaqG1bGaae<br />% yyaiaab6gacaqGKbGaae4BaiaabccacaqGLbGaaeiBaiaabccacaqG<br />% HdGaaeOCaiaabwgacaqGHbGaaeiiaiaabYgacaqGPbGaaeyBaiaabM<br />% gacaqG0bGaaeyyaiaabsgacaqGVbGaaeiiaiaabchacaqGVbGaaeOC<br />% aiaabccaaeaacaWG5bGaeyypa0JaaGinaiabgkHiTiaadIhadaahaa<br />% WcbeqaaiaaikdaaaGccaGG7aGaamyEaiabg2da9iaaicdaaeaacaWG<br />% HbGaaiykaiaabEeacaqGPbGaaeOCaiaabggacaqGGaGaaeyzaiaab6<br />% gacaqGGaGaaeiDaiaab+gacaqGYbGaaeOBaiaab+gacaqGGaGaaeiz<br />% aiaabwgacaqGGaGaaeiEaiaab2dacaqGYaaabaGaaeOyaiaabMcaca<br />% qGhbGaaeyAaiaabkhacaqGHbGaaeiiaiaabwgacaqGUbGaaeiiaiaa<br />% bshacaqGVbGaaeOCaiaab6gacaqGVbGaaeiiaiaabsgacaqGLbGaae<br />% iiaiaabIhacaqG9aGaaeylaiaabodaaeaaaeaacaqG0aGaaeOlaiaa<br />% bcfacaqGHbGaaeOCaiaabggacaqGGaGaaeyDaiaab6gacaqGHbGaae<br />% iiaiaabYgacaqGHbGaaeyBaiaabMgacaqGUbGaaeyyaiaabccacaqG<br />% WbGaaeiBaiaabggacaqGUbGaaeyyaiaabccacaqGSbGaaeyAaiaab2<br />% gacaqGPbGaaeiDaiaabggacaqGKbGaaeyyaiaabccacaqGWbGaae4B<br />% aiaabkhacaqGGaGaamyEaiabg2da9iaadAgacaGGOaGaamiEaiaacM<br />% cacaqGGaGaaeilaiaabccacaqGSbGaaeyyaiaabohacaqGGaGaaeOC<br />% aiaabwgacaqGJbGaaeiDaiaabggacaqGZbGaaeiiaiaadIhacqGH9a<br />% qpcaWGHbGaaeiiaiaabMhacaqGGaGaamiEaiabg2da9iaadkgacaqG<br />% 7aaabaGaae4CaiaabwgacaqGGaGaaeizaiaabwgacaqGMbGaaeyAai<br />% aab6gacaqGLbGaaeOBaiaabQdaaeaacaWGnbGaamyyaiaadohacaWG<br />% HbGaeyypa0JaeyOaIy7aa8qCaeaacaWGMbGaaiikaiaadIhacaGGPa<br />% GaamizaiaadIhacaGG7aGaaeiiaiabgkGi2kabg2da9iaadsgacaWG<br />% LbGaamOBaiaadohacaWGPbGaamizaiaadggacaWGKbGaaiikaiaado<br />% gacaWG0bGaamyzaiaacMcaaSqaaiaadggaaeaacaWGIbaaniabgUIi<br />% YdaakeaacaqGnbGaae4Baiaab2gacaqGLbGaaeOBaiaabshacaqGVb<br />% GaaeiiaiaabogacaqGVbGaaeOBaiaabccacaqGYbGaaeyzaiaaboha<br />% caqGWbGaaeyzaiaabogacaqG0bGaae4BaiaabccacaqGHbGaaeiiai<br />% aabYgacaqGVbGaae4CaiaabccacaqGLbGaaeOAaiaabwgacaqGZbGa<br />% aeOoaiaabccacaWGnbWaaSbaaSqaaiaadIhaaeqaaOGaeyypa0Jaey<br />% OaIy7aa8qCaeaadaWcaaqaaiaaigdaaeaacaaIYaaaaiaadAgadaah<br />% aaWcbeqaaiaaikdaaaGccaGGOaGaamiEaiaacMcacaWGKbGaamiEai<br />% aacUdacaWGnbWaaSbaaSqaaiaadMhaaeqaaOGaeyypa0JaeyOaIy7a<br />% a8qCaeaacaWG4bGaamOzaiaacIcacaWG4bGaaiykaiaadsgacaWG4b<br />% aaleaacaWGHbaabaGaamOyaaqdcqGHRiI8aOGaaiOlaaWcbaGaamyy<br />% aaqaaiaadkgaa0Gaey4kIipaaOqaaiaaboeacaqGLbGaaeOBaiaabs<br />% hacaqGYbGaae4BaiaabccacaqGKbGaaeyzaiaabccacaqGnbGaaeyy<br />% aiaabohacaqGHbGaaeOoaiaabccacaqGOaGaaeiwaiaabYcacaqGzb<br />% GaaeykaiaabccacaqG7aGaaeiiaiaabIfacaqG9aWaaSaaaeaacaWG<br />% nbWaaSbaaSqaaiaadMhaaeqaaaGcbaGaamyBaaaacaGG7aGaamywai<br />% abg2da9maalaaabaGaamytamaaBaaaleaacaWG4baabeaaaOqaaiaa<br />% d2gaaaaabaGaamyBaiabg2da9iaad2eacaWGHbGaam4Caiaadggaae<br />% aacaqGdbGaaeyyaiaabYgacaqGJbGaaeyDaiaabYgacaqGHbGaaeOC<br />% aiaabccacaqGLbGaae4CaiaabshacaqGVbGaae4CaiaabccacaqGLb<br />% GaaeiBaiaabwgacaqGTbGaaeyzaiaab6gacaqG0bGaae4Baiaaboha<br />% caqGGaGaaeiCaiaabggacaqGYbGaaeyyaiaabccacaqGSbGaaeyyai<br />% aabccacaqGMbGaaeyAaiaabEgacaqG1bGaaeOCaiaabggacaqGGaGa<br />% aeyzaiaab6gacaqGJbGaaeyzaiaabkhacaqGYbGaaeyyaiaabsgaca<br />% qGHbGaaeiiaiaabchacaqGVbGaaeOCaiaabQdaaeaacaWG5bGaey4k<br />% aSIaamiEamaaCaaaleqabaGaaGOmaaaakiabg2da9iaaiAdaaeaaca<br />% WG5bGaey4kaSIaaGOmaiaadIhacqGH9aqpcaaIZaaabaGaae4uaiaa<br />% bMgacaqGGaGaeyOaIyRaaeypaiaabgdaaaaa!A982!<br />\[<br />\begin{gathered}<br /> 3.{\text{Determine el Volumen del cuerpo de rotaci\'o n}}{\text{, cuando el \'a rea limitado por }} \hfill \\<br /> y = 4 - x^2 ;y = 0 \hfill \\<br /> a){\text{Gira en torno de x = 2}} \hfill \\<br /> {\text{b)Gira en torno de x = - 3}} \hfill \\<br /> \hfill \\<br /> {\text{4}}{\text{.Para una lamina plana limitada por }}y = f(x){\text{ }}{\text{, las rectas }}x = a{\text{ y }}x = b{\text{;}} \hfill \\<br /> {\text{se definen:}} \hfill \\<br /> Masa = \partial \int\limits_a^b {f(x)dx;{\text{ }}\partial = densidad(cte)} \hfill \\<br /> {\text{Momento con respecto a los ejes: }}M_x = \partial \int\limits_a^b {\frac{1}<br />{2}f^2 (x)dx;M_y = \partial \int\limits_a^b {xf(x)dx} .} \hfill \\<br /> {\text{Centro de Masa: (X}}{\text{,Y) ; X = }}\frac{{M_y }}<br />{m};Y = \frac{{M_x }}<br />{m} \hfill \\<br /> m = Masa \hfill \\<br /> {\text{Calcular estos elementos para la figura encerrada por:}} \hfill \\<br /> y + x^2 = 6 \hfill \\<br /> y + 2x = 3 \hfill \\<br /> {\text{Si }}\partial {\text{ = 1}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/40d7f522ee2589bbda552f702c6393af.png) Me fue como el Ass en esta T.T -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 06:22 PM
Publicado:
#5
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
PEP 4 Calculo Aplicado
Fecha 30/10/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabseacaqGHbGaaeizaiaabggacaqGGaGaaeiBaiaabgga<br />% caqGGaGaaeOraiaabwhacaqGUbGaae4yaiaabMgacaqGZdGaaeOBai<br />% aabccacaqGGaGaamOzaiaacIcacaWG4bGaaiilaiaadMhacaGGPaGa<br />% aiOoaaqaaiaadAgacaGGOaGaamiEaiaacYcacaWG5bGaaiykaiabg2<br />% da9maalaaabaGaamiEamaaCaaaleqabaGaaGOmaaaakiaadMhadaah<br />% aaWcbeqaaiaaikdaaaaakeaacaWG4bWaaWbaaSqabeaacaaIYaaaaO<br />% GaamyEamaaCaaaleqabaGaaGOmaaaakiabgUcaRiaacIcacaWG4bGa<br />% eyOeI0IaamyEaiaacMcadaahaaWcbeqaaiaaikdaaaaaaOGaai4oai<br />% aabccacaqGtbGaaeyAaiaabccacaGGOaGaamiEaiaacYcacaWG5bGa<br />% aiykaiabgcMi5kaaicdaaeaacaWGMbGaaiikaiaadIhacaGGSaGaam<br />% yEaiaacMcacqGH9aqpcaaIXaGaai4oaiaabccacaqGZbGaaeyAaiaa<br />% bccacaqGOaGaamiEaiaacYcacaWG5bGaaiykaiabg2da9iaaicdaae<br />% aacaqGfbGaae4CaiaabshacaqG1bGaaeizaiaabMgacaqGLbGaaeii<br />% aiaabohacaqG1bGaaeiiaiaabogacaqGVbGaaeOBaiaabshacaqGPb<br />% GaaeOBaiaabwhacaqGPbGaaeizaiaabggacaqGKbGaaeiiaiaabwga<br />% caqGUbGaaeiiaiaabwgacaqGSbGaaeiiaiaabIcacaqGWaGaaeilai<br />% aabcdacaqGPaGaaeiiaiaabMhacaqGGaGaaeyzaiaab6gacaqGJbGa<br />% aeyDaiaabwgacaqGUbGaaeiDaiaabkhacaqGLbGaaeiiamaalaaaba<br />% GaeyOaIyRaamOzaaqaaiabgkGi2kaadIhaaaGaaeiiaiaabMhacaqG<br />% GaWaaSaaaeaacqGHciITcaWGMbaabaGaeyOaIyRaamyEaaaacaqGGa<br />% Gaaeyzaiaab6gacaqGGaGaaeikaiaabcdacaqGSaGaaeimaiaabMca<br />% caqGGaGaaeyEaiaabccacaqGLbGaaeOBaiaabccacaqGOaGaaeymai<br />% aabYcacaqGXaGaaeykaaaaaa!BCF2!<br />\[<br />\begin{gathered}<br /> 1.{\text{Dada la Funci\'o n }}f(x,y): \hfill \\<br /> f(x,y) = \frac{{x^2 y^2 }}<br />{{x^2 y^2 + (x - y)^2 }};{\text{ Si }}(x,y) \ne 0 \hfill \\<br /> f(x,y) = 1;{\text{ si (}}x,y) = 0 \hfill \\<br /> {\text{Estudie su continuidad en el (0}}{\text{,0) y encuentre }}\frac{{\partial f}}<br />{{\partial x}}{\text{ y }}\frac{{\partial f}}<br />{{\partial y}}{\text{ en (0}}{\text{,0) y en (1}}{\text{,1)}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/02244da2741e9e5297b6d73271c9567f.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaaeOmaiaab6<br />% cacaqGGaGaae4uaiaabMgacaqGGaGaamOEaiabg2da9iaadggacaWG<br />% YbGaam4yaiaadshacaWGNbGaaiikaiaadIhacqGHRaWkcaaIYaGaam<br />% yEaiaacMcacqGHRaWkcaWGLbWaaWbaaSqabeaacaWG4bGaeyOeI0Ia<br />% aGOmaiaadMhaaaaaaa!4B99!<br />\[<br />{\text{2}}{\text{. Si }}z = arctg(x + 2y) + e^{x - 2y} <br />\]<br />](./tex/593ebd789df1c1f22a28ec1dcb03feac.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaae4qaiaab+<br />% gacaqGTbGaaeiCaiaabkhacaqG1bGaaeyzaiaabkgacaqGLbGaaeii<br />% aiaabghacaqG1bGaaeyzaiaabccacaqGZbGaaeyyaiaabshacaqGPb<br />% Gaae4CaiaabAgacaqGHbGaae4yaiaabwgacaqGGaGaaeiBaiaabgga<br />% caqGGaGaaeOCaiaabwgacaqGSbGaaeyyaiaabogacaqGPbGaae48ai<br />% aab6gacaqG6aGaaeiiaiaadQhadaWgaaWcbaGaamyEaiaadMhaaeqa<br />% aOGaeyypa0JaaGinaiaadQhadaWgaaWcbaGaamiEaiaadIhaaeqaaa<br />% aa!5F0E!<br />\[<br />{\text{Compruebe que satisface la relaci\'o n: }}z_{yy} = 4z_{xx} <br />\]<br />](./tex/4fb813e303c14ae68fd360159869d2a9.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIZa<br />% GaaiOlaiaaboeacaqGHbGaaeiBaiaabogacaqG1bGaaeiBaiaabwga<br />% caqGGaGaaeyzaiaabYgacaqGGaGaaeyBaiaabggacaqG4bGaaeyAai<br />% aab2gacaqGVbGaaeiiaiaabAhacaqGHbGaaeiBaiaab+gacaqGYbGa<br />% aeiiaiaabsgacaqGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabsgaca<br />% qGLbGaaeOCaiaabMgacaqG2bGaaeyyaiaabsgacaqGHbGaaeiiaiaa<br />% bsgacaqGPbGaaeOCaiaabwgacaqGJbGaae4yaiaabMgacaqGVbGaae<br />% OBaiaabggacaqGSbGaaeiiaiaabsgacaqGLbGaaeiiaiaabYgacaqG<br />% HbGaaeiiaiaabAgacaqG1bGaaeOBaiaabogacaqGPbGaae48aiaab6<br />% gacaqG6aaabaGaamOzaiaacIcacaWG4bGaaiilaiaadMhacaGGSaGa<br />% amOEaiaacMcacqGH9aqpcaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey<br />% OeI0IaaGioaiaadIhacaWG5bGaey4kaSIaamyEamaaCaaaleqabaGa<br />% aGOmaaaakiabgkHiTiaaiIdacaWG4bGaamOEaiabgUcaRiaadQhada<br />% ahaaWcbeqaaiaaikdaaaGccqGHsislcaaI4aGaamyEaiaadQhacaGG<br />% SaGaaeiiaiaabwgacaqGUbGaaeiiaiaabwgacaqGSbGaaeiiaiaabc<br />% hacaqG1bGaaeOBaiaabshacaqGVbGaaeiiaiaadcfacaGGOaGaaGym<br />% aiaacYcacaaIYaGaaiilaiaaiodacaGGPaGaaiOlaaqaaaqaaiaais<br />% dacaGGUaGaae4qaiaabggacaqGSbGaae4yaiaabwhacaqGSbGaaeyz<br />% aiaabccacaqGSbGaaeyyaiaabohacaqGGaGaaeyzaiaabogacaqG1b<br />% GaaeyyaiaabogacaqGPbGaae4Baiaab6gacaqGLbGaae4Caiaabcca<br />% caqGKbGaaeyzaiaabYgacaqGGaGaaeiCaiaabYgacaqGHbGaaeOBai<br />% aab+gacaqGGaGaaeiDaiaabggacaqGUbGaae4zaiaabwgacaqGUbGa<br />% aeiDaiaabwgacaqGGaGaaeiiaiaabMhacaqGGaGaaeiBaiaabggaca<br />% qGGaGaaeOCaiaabwgacaqGJbGaaeiDaiaabggacaqGGaGaaeOBaiaa<br />% b+gacaqGYbGaaeyBaiaabggacaqGSbGaaeiiaiaabggacaqGGaGaae<br />% iBaiaabggacaqGGaGaae4CaiaabwhacaqGWbGaaeyzaiaabkhacaqG<br />% MbGaaeyAaiaabogacaqGPbGaaeyzaiaabQdaaeaacaWG4bGaamyEai<br />% abgUcaRiaaikdacaWG5bGaamOEaiabgkHiTiaadIhacaWG6bWaaWba<br />% aSqabeaacaaIYaaaaOGaey4kaSIaaGymaiaaicdacqGH9aqpcaaIWa<br />% GaaiilaiaabccacaqGLbGaaeOBaiaabccacaqGLbGaaeiBaiaabcca<br />% caqGWbGaaeyDaiaab6gacaqG0bGaae4BaiaabccacaqGOaGaaeylai<br />% aabwdacaqGSaGaaeynaiaabYcacaqGXaGaaeykaaqaaaqaaiaabwda<br />% caqGUaGaaeyraiaab6gacaqGJbGaaeyDaiaabwgacaqGUbGaaeiDai<br />% aabkhacaqGLbGaaeiiaiaabwgacaqGGaGaaeyAaiaabsgacaqGLbGa<br />% aeOBaiaabshacaqGPbGaaeOzaiaabMgacaqGXbGaaeyDaiaabwgaca<br />% qGGaGaaeiBaiaab+gacaqGZbGaaeiiaiaabchacaqG1bGaaeOBaiaa<br />% bshacaqGVbGaae4CaiaabccacaqGJbGaaeOCaiaabMgacaqG0bGaae<br />% yAaiaabogacaqGVbGaae4CaiaabccacaqGKbGaaeyzaiaabccacaqG<br />% SbGaaeyyaiaabccacaqGMbGaaeyDaiaab6gacaqGJbGaaeyAaiaabo<br />% pacaqGUbGaaeOoaaqaaiaadAgacaGGOaGaamiEaiaacYcacaWG5bGa<br />% aiykaiabg2da9iaadIhadaahaaWcbeqaaiaaiodaaaGccqGHRaWkca<br />% WG5bWaaWbaaSqabeaacaaIZaaaaOGaey4kaSIaaGyoaiaadIhadaah<br />% aaWcbeqaaiaaikdaaaGccqGHsislcaaIZaGaamyEamaaCaaaleqaba<br />% GaaGOmaaaakiabgUcaRiaaigdacaaI1aGaamiEaiabgkHiTiaaiMda<br />% caWG5baaaaa!4DD5!<br />\[<br />\begin{gathered}<br /> 3.{\text{Calcule el maximo valor de la derivada direccional de la funci\'o n:}} \hfill \\<br /> f(x,y,z) = x^2 - 8xy + y^2 - 8xz + z^2 - 8yz,{\text{ en el punto }}P(1,2,3). \hfill \\<br /> \hfill \\<br /> 4.{\text{Calcule las ecuaciones del plano tangente y la recta normal a la superficie:}} \hfill \\<br /> xy + 2yz - xz^2 + 10 = 0,{\text{ en el punto ( - 5}}{\text{,5}}{\text{,1)}} \hfill \\<br /> \hfill \\<br /> {\text{5}}{\text{.Encuentre e identifique los puntos criticos de la funci\'o n:}} \hfill \\<br /> f(x,y) = x^3 + y^3 + 9x^2 - 3y^2 + 15x - 9y \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/b1e85034f96e37f6d89be0d1c05c64c8.png) La más Fácil de todas Mensaje modificado por davosalinas el Jan 19 2008, 06:27 PM -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 06:41 PM
Publicado:
#6
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
PER(Prueba Especial de Reemplazo) Calculo Aplicado
Fecha:20/11/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabcfacaqGHbGaaeOCaiaabggacaqGGaGaaeiBaiaabgga<br />% caqGGaGaaeysaiaab6gacaqG0bGaaeyzaiaabEgacaqGYbGaaeyyai<br />% aabYgacaqGGaGaaeizaiaab+gacaqGIbGaaeiBaiaabwgacaqG6aWa<br />% a8qCaeaadaWdXbqaaiaadwgadaahaaWcbeqaaiaadIhadaahaaadbe<br />% qaaiaaisdaaaaaaOGaamizaiaadIhacaWGKbGaamyEaaWcbaWaaOqa<br />% aeaacaWG5baameaacaaIZaaaaaWcbaGaaGOmaaqdcqGHRiI8aaWcba<br />% GaaeimaaqaaiaabIdaa0Gaey4kIipaaOqaaiaabggacaqGPaGaae4r<br />% aiaabkhacaqGHbGaaeOzaiaabMgacaqGXbGaaeyDaiaabwgacaqGGa<br />% GaaeyEaiaabccacaqGJbGaaeyyaiaabYgacaqGJbGaaeyDaiaabYga<br />% caqGLbGaaeiiaiaabwgacaqGSbGaaeiiaiaabggacaqGYbGaaeyzai<br />% aabggacaqGGaGaaeizaiaabwgacaqGSbGaaeiiaiaabsgacaqGVbGa<br />% aeyBaiaabMgacaqGUbGaaeyAaiaab+gaaeaacaqGIbGaaeykaiaabo<br />% eacaqGHbGaaeiBaiaabogacaqG1bGaaeiBaiaabwgacaqGGaGaaeiB<br />% aiaabggacaqGGaGaaeysaiaab6gacaqG0bGaaeyzaiaabEgacaqGYb<br />% GaaeyyaiaabYgaaeaaaeaacaqGYaGaaeOlaiaabYeacaqGHbGaaeii<br />% aiaabMeacaqGUbGaaeiDaiaabwgacaqGNbGaaeOCaiaabggacaqGSb<br />% GaaeiiamaapifabaWaaOaaaeaacaaIXaGaeyOeI0IaamiEamaaCaaa<br />% leqabaGaaGOmaaaakiabgkHiTiaadMhadaahaaWcbeqaaiaaikdaaa<br />% aabeaaaeaacaqGebaabeqdcqGHRiI8cqGHRiI8aOGaamizaiaadgea<br />% caGGSaGaaeiiaiaabofacaqGPbGaaeiiaiaadseacqGH9aqpdaGada<br />% qaaiaacIcacaWG4bGaaiilaiaadMhacaGGPaGaai4laiaadIhadaah<br />% aaWcbeqaaiaaikdaaaGccqGHRaWkcaWG5bWaaWbaaSqabeaacaaIYa<br />% aaaOGaeyizImQaaGymaaGaay5Eaiaaw2haaiaabccacaqGsbGaaeyz<br />% aiaabchacaqGYbGaaeyzaiaabohacaqGLbGaaeOBaiaabshacaqGHb<br />% GaaeiiaiaabwhacaqGUbGaaeiiaaqaaiaabAhacaqGVbGaaeiBaiaa<br />% bwhacaqGTbGaaeyzaiaab6gaaeaacaqGHbGaaeykaiaabEeacaqGYb<br />% GaaeyyaiaabAgacaqGPbGaaeyCaiaabwhacaqGLbGaaeiiaiaabMha<br />% caqGGaGaaeOCaiaabwgacaqGJbGaae4Baiaab6gacaqGVbGaaeOEai<br />% aabogacaqGHbGaaeiiaiaabwgacaqGSbGaaeiiaiaabohacaqGVbGa<br />% aeiBaiaabMgacaqGKbGaae4BaaqaaiaabkgacaqGPaGaae4qaiaabg<br />% gacaqGSbGaae4yaiaabwhacaqGSbGaaeyzaiaabccacaqGLbGaaeiB<br />% aiaabccacaqGwbGaae4BaiaabYgacaqG1bGaaeyBaiaabwgacaqGUb<br />% aabaaabaGaae4maiaab6cacaqGdbGaaeyyaiaabYgacaqGJbGaaeyD<br />% aiaabYgacaqGLbGaaeiiaiaabwgacaqGSbGaaeiiaiaabgoacaqGYb<br />% GaaeyzaiaabggacaqGGaGaaeizaiaabwgacaqGGaGaaeiBaiaabgga<br />% caqGGaGaaeiCaiaabggacaqGYbGaaeiDaiaabwgacaqGGaGaaeizai<br />% aabwgacaqGSbGaaeiiaiaabchacaqGHbGaaeOCaiaabggacaqGIbGa<br />% ae4BaiaabYgacaqGVbGaaeyAaiaabsgacaqGLbGaaeiiaiaadQhacq<br />% GH9aqpcaWG4bWaaWbaaSqabeaacaaIYaaaaOGaey4kaSIaamyEamaa<br />% CaaaleqabaGaaGOmaaaakiaabccacaqGXbGaaeyDaiaabwgacaqGGa<br />% Gaae4CaiaabwgacaqGGaGaaeyzaiaab6gacaqGJbGaaeyDaiaabwga<br />% caqGUbGaaeiDaiaabkhacaqGHbaabaGaaeOyaiaabggacaqGQbGaae<br />% 4BaiaabccacaqGLbGaaeiBaiaabccacaqGWbGaaeiBaiaabggacaqG<br />% UbGaae4BaiaabccacaqG6bGaaeypaiaabMdaaeaaaeaacaqG0aGaae<br />% OlaiaabYeacaqGHbGaaeiiaiaabshacaqGLbGaaeyBaiaabchacaqG<br />% LbGaaeOCaiaabggacaqG0bGaaeyDaiaabkhacaqGHbGaaeiiaiaabw<br />% gacaqGUbGaaeiiaiaabwhacaqGUbGaaeiiaiaabchacaqG1bGaaeOB<br />% aiaabshacaqGVbGaaeiiaiaabcfacaqGOaGaaeiEaiaabYcacaqG5b<br />% GaaeilaiaabQhacaqGPaGaaeiiaiaabwgacaqGZbGaaeiDaiaabgga<br />% caqGGaGaaeizaiaabggacaqGKbGaaeyyaiaabccacaqGWbGaae4Bai<br />% aabkhaaeaacaWGubGaaiikaiaadIhacaGGSaGaamyEaiaacYcacaWG<br />% 6bGaaiykaiabg2da9iaaikdacaaIWaGaaGimaiaadwgadaahaaWcbe<br />% qaaiabgkHiTiaacIcacaWG4bWaaWbaaWqabeaacaaIYaaaaSGaey4k<br />% aSIaaG4maiaadMhadaahaaadbeqaaiaaikdaaaWccqGHRaWkcaaI5a<br />% GaamOEamaaCaaameqabaGaaGOmaaaaliaacMcaaaaakeaacaqGHbGa<br />% aeykaiaabweacaqGUbGaae4yaiaabwhacaqGLbGaaeOBaiaabshaca<br />% qGYbGaaeyzaiaabccacaqGSbGaaeyyaiaabccacaqGYbGaaeyyaiaa<br />% bQhacaqGZdGaaeOBaiaabccacaqGKbGaaeyzaiaabccacaqGJbGaae<br />% yyaiaab2gacaqGIbGaaeyAaiaab+gacaqGGaGaaeizaiaabwgacaqG<br />% GaGaaeiBaiaabggacaqGGaGaaeiDaiaabwgacaqGTbGaaeiCaiaabw<br />% gacaqGYbGaaeyyaiaabshacaqG1bGaaeOCaiaabggacaqGGaGaaeyz<br />% aiaab6gacaqGGaGaaeyzaiaabYgacaqGGaGaaeiCaiaabwhacaqGUb<br />% GaaeiDaiaab+gacaqGGaGaaeiuaiaabIcacaqGYaGaaeilaiaab2ca<br />% caqGXaGaaeilaiaabkdacaqGPaGaaeiiaiaabwgacaqGUbGaaeiiaa<br />% qaaiaabsgacaqGPbGaaeOCaiaabwgacaqGJbGaae4yaiaabMgacaqG<br />% VbGaaeOBaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeODaiaabg<br />% gacaqGGaGaaeyyaiaabYgacaqGGaGaaeiCaiaabwhacaqGUbGaaeiD<br />% aiaab+gacaqGGaGaaeyuaiaabIcacaqGZaGaaeilaiaab2cacaqGZa<br />% GaaeilaiaabodacaqGPaGaaeOlaaqaaiaabkgacaqGPaGaaeiraiaa<br />% bwgacaqG0bGaaeyzaiaabkhacaqGTbGaaeyAaiaab6gacaqGLbGaae<br />% iiaiaabYgacaqGHbGaaeiiaiaab2gacaqGHbGaaeiEaiaabMgacaqG<br />% TbGaaeyyaiaabccacaqGYbGaaeyyaiaabQhacaqGZdGaaeOBaiaabc<br />% cacaqGKbGaaeyzaiaabccacaqGJbGaaeyyaiaab2gacaqGIbGaaeyA<br />% aiaab+gacaqGGaGaaeyzaiaab6gacaqGGaGaaeizaiaabMgacaqGJb<br />% GaaeiAaiaab+gacaqGGaGaaeiCaiaabwhacaqGUbGaaeiDaiaab+ga<br />% aaaa!16E9!<br />\[<br />\begin{gathered}<br /> 1.{\text{Para la Integral doble:}}\int\limits_{\text{0}}^{\text{8}} {\int\limits_{\sqrt[3]{y}}^2 {e^{x^4 } dxdy} } \hfill \\<br /> {\text{a)Grafique y calcule el area del dominio}} \hfill \\<br /> {\text{b)Calcule la Integral}} \hfill \\<br /> \hfill \\<br /> {\text{2}}{\text{.La Integral }}\iint\limits_{\text{D}} {\sqrt {1 - x^2 - y^2 } }dA,{\text{ Si }}D = \left\{ {(x,y)/x^2 + y^2 \leqslant 1} \right\}{\text{ Representa un }} \hfill \\<br /> {\text{volumen}} \hfill \\<br /> {\text{a)Grafique y reconozca el solido}} \hfill \\<br /> {\text{b)Calcule el Volumen}} \hfill \\<br /> \hfill \\<br /> {\text{3}}{\text{.Calcule el \'a rea de la parte del paraboloide }}z = x^2 + y^2 {\text{ que se encuentra}} \hfill \\<br /> {\text{bajo el plano z = 9}} \hfill \\<br /> \hfill \\<br /> {\text{4}}{\text{.La temperatura en un punto P(x}}{\text{,y}}{\text{,z) esta dada por}} \hfill \\<br /> T(x,y,z) = 200e^{ - (x^2 + 3y^2 + 9z^2 )} \hfill \\<br /> {\text{a)Encuentre la raz\'o n de cambio de la temperatura en el punto P(2}}{\text{, - 1}}{\text{,2) en }} \hfill \\<br /> {\text{direccion que va al punto Q(3}}{\text{, - 3}}{\text{,3)}}{\text{.}} \hfill \\<br /> {\text{b)Determine la maxima raz\'o n de cambio en dicho punto}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/2cc0e7f590fcc0ea45beccb845a3c834.png)
-------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 06:54 PM
Publicado:
#7
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
Examen I: Calculo Aplicado
Fecha:27/11/2007 ![TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaaIXa<br />% GaaiOlaiaabggacaqGPaGaaeiiaiaabcfacaqGYbGaaeyDaiaabwga<br />% caqGIbGaaeyzaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeiBai<br />% aabggacaqGGaGaae4uaiaabwgacaqGYbGaaeyAaiaabwgacaqG6aWa<br />% aabCaeaadaWcaaqaaiaabodadaahaaWcbeqaaiaab6gaaaGccaWGUb<br />% WaaWbaaSqabeaacaaIYaaaaaGcbaGaamOBaiaacgcaaaGaaeiiaiaa<br />% bweacaqGZbGaaeiiaiaabogacaqGVbGaaeOBaiaabAhacaqGLbGaae<br />% OCaiaabEgacaqGLbGaaeOBaiaabshacaqGLbaaleaacaqGWaaabaGa<br />% eyOhIukaniabggHiLdaakeaacaWGIbGaaiykaiaabseacaqGLbGaae<br />% iDaiaabwgacaqGYbGaaeyBaiaabMgacaqGUbGaaeyzaiaabccacaqG<br />% LbGaaeiBaiaabccacaqGPbGaaeOBaiaabshacaqGLbGaaeOCaiaabA<br />% hacaqGHbGaaeiBaiaab+gacaqGGaGaaeizaiaabwgacaqGGaGaae4y<br />% aiaab+gacaqGUbGaaeODaiaabwgacaqGYbGaae4zaiaabwgacaqGUb<br />% Gaae4yaiaabMgacaqGHbGaaeiiaiaabsgacaqGLbGaaeiiaiaabYga<br />% caqGHbGaaeiiaiaabohacaqGLbGaaeOCaiaabMgacaqGLbGaaeOoai<br />% aabccadaaeabqaamaalaaabaWaaeWaaeaacaWG4bGaey4kaSIaaGOm<br />% aaGaayjkaiaawMcaamaaCaaaleqabaGaamOBaaaaaOqaaiaad6gaca<br />% aI0aWaaWbaaSqabeaacaWGUbaaaaaaaeqabeqdcqGHris5aaGcbaaa<br />% baGaaGOmaiaac6cacaqGfbGaaeOBaiaabogacaqG1bGaaeyzaiaab6<br />% gacaqG0bGaaeOCaiaabwgacaqGGaGaaeyzaiaab6gacaqGGaGaaeiB<br />% aiaabggacaqGGaGaae4CaiaabwhacaqGWbGaaeyzaiaabkhacaqGMb<br />% GaaeyAaiaabogacaqGPbGaaeyzaiaabQdacaqGGaGaamiEaiaadMha<br />% daahaaWcbeqaaiaaikdaaaGccaqG6bWaaWbaaSqabeaacaqGZaaaaO<br />% GaaeypaiaabkdacaqGGaGaaeilaiaabYgacaqGVbGaae4Caiaabcca<br />% caqGWbGaaeyDaiaab6gacaqG0bGaae4BaiaabohacaqGGaGaaeyBai<br />% aabggacaqGZbGaaeiiaiaabogacaqGLbGaaeOCaiaabogacaqGHbGa<br />% aeOBaiaab+gacaqGZbGaaeiiaiaabggacaqGSbGaaeiiaiaab+gaca<br />% qGYbGaaeyAaiaabEgacaqGLbGaaeOBaiaabYcacaqGGaaabaGaaeyy<br />% aiaabchacaqGSbGaaeyAaiaabogacaqGHbGaaeOBaiaabsgacaqGVb<br />% GaaeiiaiaabYgacaqGVbGaae4CaiaabccacaqGTbGaaeyDaiaabYga<br />% caqG0bGaaeyAaiaabchacaqGSbGaaeyAaiaabogacaqGHbGaaeizai<br />% aab+gacaqGYbGaaeyzaiaabohacaqGGaGaaeizaiaabwgacaqGGaGa<br />% aeitaiaabggacaqGNbGaaeOCaiaabggacaqGUbGaae4zaiaabwgaca<br />% qGUaaabaaabaGaae4maiaab6cacaqGGaGaaeyraiaabYgacaqGGaGa<br />% ae4yaiaabwhacaqGLbGaaeOCaiaabchacaqGVbGaaeiiaiaabwgaca<br />% qGZbGaaeiDaiaabggacaqGGaGaaeiBaiaabMgacaqGTbGaaeyAaiaa<br />% bshacaqGHbGaaeizaiaab+gacaqGGaGaaeiCaiaab+gacaqGYbGaae<br />% iiaiaabYgacaqGHbGaae4CaiaabccacaqGZbGaaeyDaiaabchacaqG<br />% LbGaaeOCaiaabAgacaqGPbGaae4yaiaabMgacaqGLbGaae4Caiaabc<br />% cacaqG6aaabaGaamOEaiabg2da9maalaaabaGaaGOmaaqaaiaadIha<br />% daahaaWcbeqaaiaaikdaaaaaaOGaai4oaiaadMhacqGH9aqpcaaIYa<br />% GaamiEaiabgkHiTiaadIhadaahaaWcbeqaaiaaikdaaaGccaGG7aGa<br />% amiEaiabg2da9maalaaabaGaaGymaaqaaiaaikdaaaGaai4oaiaadI<br />% hacqGH9aqpdaWcaaqaaiaaiodaaeaacaaIYaaaaiaacUdacaWG5bGa<br />% eyypa0JaaGimaiaacUdacaWG6bGaeyypa0JaaGimaaqaaiaabggaca<br />% qGPaGaae4raiaabkhacaqGHbGaaeOzaiaabMgacaqGJbGaaeyyaiaa<br />% bkhacaqGGaGaaeyzaiaabYgacaqGGaGaae4Caiaab+gacaqGSbGaae<br />% yAaiaabsgacaqGVbGaaeilaiaabccacaqGGaGaaeOyaiaabMcacaqG<br />% GaGaae4qaiaabggacaqGSbGaae4yaiaabwhacaqGSbGaaeyzaiaabc<br />% cacaqGLbGaaeiBaiaabccacaqGwbGaae4BaiaabYgacaqG1bGaaeyB<br />% aiaabwgacaqGUbaabaaabaGaaeinaiaab6cacaqGvbGaaeOBaiaabc<br />% cacaqGdbGaaeyyaiaab2gacaqGWbGaae4BaiaabccacaqGKbGaaeyz<br />% aiaabccacaqGMbGaaeyDaiaabwgacaqGYbGaaeOEaiaabggacaqGGa<br />% GaaeyzaiaabohacaqG0bGaaeyyaiaabccacaqGKbGaaeyyaiaabsga<br />% caqGVbGaaeiiaiaabchacaqGVbGaaeOCaiaabQdacaWGgbGaaiikai<br />% aadcfacaGGPaGaeyypa0JaaiikaiaadwgadaahaaWcbeqaaiaadIha<br />% aaGccaGGSaGaamyzamaaCaaaleqabaGaamyEaaaakiaacYcacaWGLb<br />% WaaWbaaSqabeaacaWG6baaaOGaaiykaiaac6caaeaacaqGHbGaaeyk<br />% aiaabcfacaqGYbGaaeyDaiaabwgacaqGIbGaaeyzaiaabccacaqGXb<br />% GaaeyDaiaabwgacaqGGaGaaeyzaiaabohacaqGGaGaaeyDaiaab6ga<br />% caqGGaGaae4qaiaabggacaqGTbGaaeiCaiaab+gacaqGGaGaae4qai<br />% aab+gacaqGUbGaae4CaiaabwgacaqGYbGaaeODaiaabggacaqG0bGa<br />% aeyAaiaabAhacaqGVbGaaeiiaiaabIgacaqGHbGaaeiBaiaabYgaca<br />% qGHbGaaeOBaiaabsgacaqGVbGaaeiiaiaabwgacaqGSbGaaeiiaiaa<br />% bchacaqGVbGaaeiDaiaabwgacaqGUbGaae4yaiaabMgacaqGHbGaae<br />% iBaiaab6caaeaacaqGIbGaaeykaiaaboeacaqGHbGaaeiBaiaaboga<br />% caqG1bGaaeiBaiaabwgacaqGGaGaaeyzaiaabYgacaqGGaGaaeiDai<br />% aabkhacaqGHbGaaeOyaiaabggacaqGQbGaae4BaiaabccacaqGXbGa<br />% aeyDaiaabwgacaqGGaGaaeOCaiaabwgacaqGHbGaaeiBaiaabMgaca<br />% qG6bGaaeyyaiaabccacaqGHbGaaeiBaiaabccacaqGYbGaaeyzaiaa<br />% bogacaqGVbGaaeOCaiaabkhacaqGLbGaaeOCaiaabccacaqGHbGaae<br />% iiaiaabYgacaqGVbGaaeiiaiaabYgacaqGHbGaaeOCaiaabEgacaqG<br />% VbGaaeiiaiaabsgacaqGLbGaaeiiaiaabYgacaqGHbGaaeiiaiaabo<br />% gacaqG1bGaaeOCaiaabAhacaqGHbGaaeiiaiaabggacaqGSbGaaeyy<br />% aiaabkgacaqGLbGaaeyyaiaabsgacaqGHbGaaeOoaaqaaiaadIhacq<br />% GH9aqpcaWG0bGaaiilaiaadMhacqGH9aqpcaWG0bWaaWbaaSqabeaa<br />% caaIYaaaaOGaaiilaiaadQhacqGH9aqpcaWG0bWaaWbaaSqabeaaca<br />% aIZaaaaOGaaeiiaiaabccacaqGKbGaaeyzaiaabohacaqGKbGaaeyz<br />% aiaabccacaqGOaGaaeimaiaabYcacaqGWaGaaeilaiaabcdacaqGPa<br />% GaaeiiaiaabggacaqGGaGaaeikaiaabkdacaqGSaGaaeinaiaabYca<br />% caqG4aGaaeykaaaaaa!2D6C!<br />\[<br />\begin{gathered}<br /> 1.{\text{a) Pruebe que la Serie:}}\sum\limits_{\text{0}}^\infty {\frac{{{\text{3}}^{\text{n}} n^2 }}<br />{{n!}}{\text{ Es convergente}}} \hfill \\<br /> b){\text{Determine el intervalo de convergencia de la serie: }}\sum {\frac{{\left( {x + 2} \right)^n }}<br />{{n4^n }}} \hfill \\<br /> \hfill \\<br /> 2.{\text{Encuentre en la superficie: }}xy^2 {\text{z}}^{\text{3}} {\text{ = 2 }}{\text{,los puntos mas cercanos al origen}}{\text{, }} \hfill \\<br /> {\text{aplicando los multiplicadores de Lagrange}}{\text{.}} \hfill \\<br /> \hfill \\<br /> {\text{3}}{\text{. El cuerpo esta limitado por las superficies :}} \hfill \\<br /> z = \frac{2}<br />{{x^2 }};y = 2x - x^2 ;x = \frac{1}<br />{2};x = \frac{3}<br />{2};y = 0;z = 0 \hfill \\<br /> {\text{a)Graficar el solido}}{\text{, b) Calcule el Volumen}} \hfill \\<br /> \hfill \\<br /> {\text{4}}{\text{.Un Campo de fuerza esta dado por:}}F(P) = (e^x ,e^y ,e^z ). \hfill \\<br /> {\text{a)Pruebe que es un Campo Conservativo hallando el potencial}}{\text{.}} \hfill \\<br /> {\text{b)Calcule el trabajo que realiza al recorrer a lo largo de la curva alabeada:}} \hfill \\<br /> x = t,y = t^2 ,z = t^3 {\text{ desde (0}}{\text{,0}}{\text{,0) a (2}}{\text{,4}}{\text{,8)}} \hfill \\ <br />\end{gathered} <br />\]<br />](./tex/2b3012711d7af1e49fd43bf84abb6fc4.png)
-------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 06:55 PM
Publicado:
#8
|
|
|
Dios Matemático Grupo: Usuario FMAT Mensajes: 234 Registrado: 4-January 07 Desde: Mi PC Miembro Nº: 3.513 Nacionalidad: Colegio/Liceo: Sexo: |
Esas son todas las Pruebas de Calculo Aplicado del 2007. En Marzo, cuando me consiga el Examen II lo subo.
Saludos y ojala que los caxorros y no tan caxorros disfruten este material Saludos DavE -------------------- "Alguna vez has sentido que darías tu vida por alguien, Piensalo dos veces Antes de Entregarla, porque nunca sabras si dicha persona aprovechara todo lo que le estas dando"
"El cigarrillo y las Matemáticas se parecen en dos cosas, Ambos me dan placer al Tenerlos en mis manos, y cuando los termino quiero más. Pero lo bueno es que la Matemática no me mata" Estudiante de II año - Ingenieria Civil Industrial |
|
|
|
|
Jan 19 2008, 09:06 PM
Publicado:
#9
|
|
 Staff FMAT  Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo: |
CITA(davosalinas @ Jan 19 2008, 08:41 PM)  ![TEX: <br />\[<br />\begin{gathered}<br /> {\text{2}}{\text{.La Integral }}\iint\limits_{\text{D}} {\sqrt {1 - x^2 - y^2 } }dA,{\text{ Si }}D = \left\{ {(x,y)/x^2 + y^2 \leqslant 1} \right\}{\text{ Representa un }} \hfill \\<br /> {\text{volumen}} \hfill \\<br /> {\text{b)Calcule el Volumen}} \hfill \\<br />\end{gathered} <br />\]<br />](./tex/342958d575d916046d579617d8e54126.png) 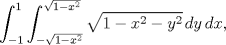Tenemos  que es un círculo entero. Aplicamos la transformación polar y queda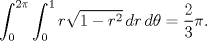 Saludos 
|
|
|
|
|
Jan 20 2008, 12:48 PM
Publicado:
#10
|
|
|
Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad: Sexo: |
CITA(davosalinas @ Jan 19 2008, 07:12 PM) ![TEX: <br />\[<br />\begin{gathered}<br /> 2.{\text{ Pruebe que la ecuaci\'o n:}} \hfill \\<br /> 1 - x^2 (y') - xy + 1 = 0,{\text{ se Cumple tanto para }} \hfill \\<br /> y = \frac{{\ln (x + \sqrt {x^2 - 1} )}}<br />{{\sqrt {x^2 - 1} }},{\text{ como tambi\'e n para: }}y = \frac{{Arc\cos (x)}}<br />{{\sqrt {1 - x^2 } }}.<br />\end{gathered} <br />\]<br />](./tex/8f1797ddb89b5315576cade82a356252.png) 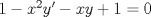Debe haber un error de tipeo en la ecuación diferencial puesto que la solución para  es 
|
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 01:47 PM |
