|
|
|
|
|
|
|
  |
 Feb 2 2006, 01:49 AM Feb 2 2006, 01:49 AM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Consideremos un triangulo
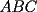 y un punto y un punto 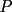 interior a el tal que: interior a el tal que: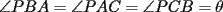 tal cual lo muestra la figura.  El angulo 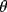 para el cual es posible esta construccion se llama angulo de Brocard. para el cual es posible esta construccion se llama angulo de Brocard.Se pide probar que este angulo en efecto existe y cumple con la siguiente relacion. 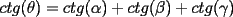 Suerte y veamos que tal les va con este bonito desafio -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 1 2007, 09:45 PM Feb 1 2007, 09:45 PM
Publicado:
#2
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
Antes de comenzar aclaro que esta demostración no es mía, por tanto no puedo vanagloriarme de algo que no hice, ante los demás.
Lo que sí me deja satisfecho, es compartir esta demostración (breve y sencilla por lo demás) con ustedes Construcciones auxiliares:

|
|
|
|
 Feb 1 2007, 09:58 PM Feb 1 2007, 09:58 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 817 Registrado: 28-May 06 Desde: maipú, santiago. Miembro Nº: 1.210 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
CITA Antes de comenzar aclaro que esta demostración no es mía, por tanto no puedo vanagloriarme de algo que no hice, ante los demás. Lo que sí me deja satisfecho, es compartir esta demostración (breve y sencilla por lo demás) con ustedes Tal vez se me fue algo, pero creo que para esa demostración se asume que el ángulo de Brocard existe, por lo que faltaría probar eso aún. Saludos. -------------------- Estudiante de 5º año de Ingeniería Civil Industrial en la U. de Chile
|
|
|
|
 Feb 1 2007, 10:01 PM Feb 1 2007, 10:01 PM
Publicado:
#4
|
|
 Staff FMAT Grupo: Super Moderador Mensajes: 8.124 Registrado: 21-May 06 Miembro Nº: 1.156 Nacionalidad:  Sexo:  |
No me nace cómo hacerlo A la espera de que alguien más fogueado lo haga |
|
|
|
 Feb 18 2007, 04:08 PM Feb 18 2007, 04:08 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad:  Universidad:  Sexo:  |
--------------------    |
|
|
|
 Apr 10 2007, 01:30 PM Apr 10 2007, 01:30 PM
Publicado:
#6
|
|
 Dios Matemático Grupo: Usuario FMAT Mensajes: 374 Registrado: 16-September 06 Desde: New Haven, CT, USA. Miembro Nº: 2.275 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solución Correcta
A resueltos. Saludos |
|
|
|
 Dec 25 2011, 06:14 PM Dec 25 2011, 06:14 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Hola! xD quería revivir este topic para mostrarles una construcción sencilla del punto de Brocard (de ambos)
 fmat.png ( 18.02k )
Número de descargas: 0
fmat.png ( 18.02k )
Número de descargas: 0 Lo entretenido de esto es que los dos puntos de Brocard son conjugados isogonales; pero por más que he buscado no encuentro apuntes relacionados al tema (todos "nombran el hecho" pero nadie le dedica un estudio serio) así que si alguien tiene referencias buenas del tema puchas que se raje con los links Mensaje modificado por Kaissa el Dec 25 2011, 07:21 PM -------------------- |
|
|
|
 Jan 26 2012, 02:51 PM Jan 26 2012, 02:51 PM
Publicado:
#8
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 2 Registrado: 26-January 12 Miembro Nº: 100.617 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Estimados, una referencia completa puede verse en uno de los libros de Ross Honsberger: "Episodes of 18 and 19 ..."
Una joya, que me llevo por primera vez a los puntos de Brocard. El tema lo trabaje en varias oportunidades como una de los ejercicios de cierre de la Introducción a la Geometría Métrica, ya que para su resolución se ponen en juego varios elementos e imágenes conceptuales como los ángulos semi inscriptos. En mi propuesta, partía de la definición y luego de que en el marco del laboratorio se propusiese la construcción, volviamos a otro problema, (en el cual se encuentra no uno sino que dos puntos de estas característias: Considerar en un ABC cualquiera, las circuferencias que son tangentes a uno de los lados en un vértice y pasan por el tercer vértice. Tenemos así 6 circunferencias, pero si las tomo de a tres en sentido horario o antihorario cada uno de estas ternes son concurrentes en un punto, que será luego un punto de Brocard. (Es decir considera las circunferencia C1, que es tangente a AB en A y pasa por C; C2, que es tangente a BC en B y pasa por A y C3 que será tangente a CA en C y pasa por B). Si consideramos las tres restantes tendremos un segundo punto de Brocard. l A continuación se realizaba el cálculo del ángulo de Brocard, tal como se demostro en el foro, con lo cual y visto el resultado se pude deducir que el valor del mismo depende solo del triángulo y ver ademas para ambos puntos hallados se trata del mismo valor. Como siempre, hay mucho mas para ver en esta configuración Saludos |
|
|
|
 Aug 1 2012, 01:49 PM Aug 1 2012, 01:49 PM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 513 Registrado: 25-April 08 Desde: CSMC Miembro Nº: 21.189 Nacionalidad:  Colegio/Liceo:  Sexo:  |
He descubierto un par de cosas, Si
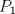 y y 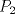 son los puntos de Brocard con angulos son los puntos de Brocard con angulos  y y 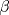 respectivamente, entonces respectivamente, entoncesComo bien se dijo anteriormente, 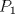 y y 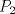 son conjugados isogonales y ambos estan a la misma distancia respecto de circuncentro, esto es son conjugados isogonales y ambos estan a la misma distancia respecto de circuncentro, esto es 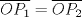 . .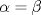 . .Y lo siguiente es de lo mas choro, atencion! 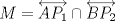 , , 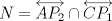 y y 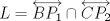 , entonces el triangulo , entonces el triangulo 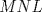 es semejante al triangulo es semejante al triangulo 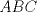 y... y... 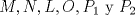 son conciclicos son conciclicos "He encontrado una demostración realmente admirable, pero el margen de esta firma es muy pequeña para ponerla" naah mentira, todo gracias a Geogebra  Brocard.png ( 47.52k )
Número de descargas: 2
Brocard.png ( 47.52k )
Número de descargas: 2-------------------- FunGeometry
SIEMPRE CON LAS MEJORES INTENCIONES DE AYUDAR. ATTE. NABODORBUCO EL TERCER OJO GoGeometry LA IDEA ES QUE NO ESPERES QUE FMAT RESUELVA TUS TAREAS, ESCRIBE SIEMPRE CUALES SON TUS INQUIETUDES |
|
|
|
 Aug 1 2012, 09:32 PM Aug 1 2012, 09:32 PM
Publicado:
#10
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 9.897 Registrado: 6-April 08 Miembro Nº: 19.238 Nacionalidad:  Colegio/Liceo:  Sexo:  |
"He encontrado una demostración realmente admirable, pero el margen de esta firma es muy pequeña para ponerla" Conozco de lejos esa propiedad. Edito!!!! mira: agarra tu figura y dibujale las circunferencias que muestro en mi diagrama; y se te va a hacer fácil probar la ciclicidad con proyectiva. Mensaje modificado por Kaissa el Aug 1 2012, 09:44 PM -------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 08:55 PM |









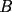 trazamos una paralela al lado
trazamos una paralela al lado 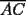
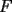 .
.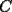 con
con 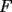 y a su vez por este último punto bajamos una perpendicular a la prolongación del lado
y a su vez por este último punto bajamos una perpendicular a la prolongación del lado 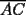 obteniéndose el punto
obteniéndose el punto 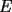 .
.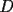 la proyección ortogonal de
la proyección ortogonal de 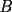 sobre el lado
sobre el lado