Potencias - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa de Enseñanza Básica > 2º Ciclo > 8º Básico > Contenidos 8º Básico

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Potencias, algo basico..

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 7 2008, 02:18 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $\textbf{Se llama potencia}$: a toda multiplicacion de factores iguales. \\ \\ En general $\forall a \in\mathbb{R}, n\in\mathbb{Z}$, se cumple que $$\underbrace{a\cdot a \cdot a \cdots a}_{n \text{ veces}}=a^n$$ \\ $\textbf{Observaci\'on}$: el signo de una potencia depende del signo de la base y la paridad del exponente:\\<br />$\begin{aligned} a^n \Rightarrow &\text{ positivo si } a\in\mathbb{N} \text{ y si } n \text{ par o impar} \\ &\text{ positivo si } a\in\mathbb{Z}^- \text{ y si } n \text{ es par} \\ &\text{ negativo si } a\in\mathbb{Z}^- \text{ y si } n \text{ es impar } \end{aligned}$\\<br />$\textbf{Potencia de base racional y exponente natural}$: segun la definici\'on de potencia podemos decir: $$\left( \dfrac{a}{b} \right)^n=\underbrace{\dfrac{a}{b} \cdot \dfrac{a}{b} \cdots \dfrac{a}{b}}_{n \text{ veces}} =\dfrac{a^n}{b^n}$$ \\ Es decir, $\left( \dfrac{a}{b} \right)^n = \dfrac{a^n}{b^n}$. Un ejemplo para dejar claro:\\ $\left( \dfrac{(-3)}5 \right)^3=\dfrac{(-3)^3}{5^3}=\dfrac{-27}{125}$. \\ $\textbf{Potencia de exponente negativo}$: supongamos que tenemos $a^{-5}$. Segun la definicion de potencia se puede escribir: $\underbrace{a \cdot a \cdot a \ldots}_{-5 \text{ veces}}$, lo que es absurdo. Sean $a\in\mathbb{R}, a\not=0, -n\in\mathbb{Z}^-$, luego, tenemos: $$a^{-n}= \left( \dfrac{1}{a}\right)^n$$ y si el numero fuera racional, sea $b\in\mathbb{Z}, b\not=0$ $$\left(\dfrac{a}{b}\right)^{-n}=\dfrac{a^{-n}}{b^{-n}}=\dfrac{\left(\dfrac{1}{a}\right)^n}{\left(\dfrac{1}{b}\right)^n}=\dfrac{\dfrac{1}{a^n}}{\dfrac{1}{b^n}}=\dfrac{b^n}{a^n}$$ es decir, $\left( \dfrac{a}{b} \right)^{-n}=\dfrac{b^n}{a^n}=\left( \dfrac{b}{a} \right)^n$. Nuevamente un ejemplo para dejar claro:$ $TEX: \noindent $\left( \dfrac{6}{5} \right)^{-3}=\left( \dfrac{5}{6} \right)^3=\dfrac{5^3}{6^3}=\dfrac{125}{216} \\ 4^{-2}=\left(\dfrac{1}{4}\right)^2=\dfrac1{4^2}=\dfrac1{16}$ \\ $\textbf{Propiedades de las potencias}$:\\ 1. Potencia de exponente cero: $$a^0=1, \forall a\in\mathbb{R}, a\not=0$$ Ejemplo: $\pi^0=1$ \\ 2. Potencia de exponente uno: $$a^1=a, \forall a\in\mathbb{R}$$ Ejemplo: $478^1=478$ \\ 3. Potencia de una potencia: $$(a^n)^m=a^{nm}$$ Ejemplo: $(2^4)^2=2^8=256$ \\ 4. Multiplicacion de potencias de igual base: $$a^n\cdot a^m=a^{n+m}, \forall a\in\mathbb{R}, n,m \in\mathbb{Z}$$ Demostracion: $$a^n\cdot a^m=\underbrace{a\cdot a\cdot a\cdots a}_{n \text{ veces}}\cdot \underbrace{a\cdots a}_{m \text{ veces}}=\underbrace{a\cdots a}_{n+m \text{ veces}}= a^{n+m}$$ Ejemplo: $4^3\cdot4^2=(4\cdot4\cdot4)\cdot(4\cdot4)=4^5$, o bien $4^3\cdot4^2=4^{3+2}=4^5$ \\ 5. Divisi\'on de potencias de igual base: $$a^n \div a^m=a^{n-m}, \forall a \in\mathbb{R}, a\not=0, n,m\in\mathbb{Z}$$ Demostraci\'on: $$a^n \div a^m=\dfrac{a^n}{a^m}=\dfrac{\underbrace{a\cdots a}_{n \text{ veces}}}{\underbrace{a\cdots a}_{m \text{ veces}}} ()$$ en $()$, simplificamos, si $n\ge m$, no hay problemas para simplificar y queda $$\dfrac{\underbrace{a\cdots a}_{n-m \text{ veces}}}1=a^{n-m}$$ Si $n<m$, entonces queda$ $TEX: \noindent $$\dfrac{1}{\underbrace{a \cdots a}_{m-n \text{ veces}}}=\dfrac{1}{a^{m-n}}=(a^{m-n})^{-1}= a^{n-m}$$ demostrando lo pedido. \\ Ejemplo: $\dfrac{5^4}{5^8}=\dfrac{5\cdot5\cdot5\cdot5}{5\cdot5\cdot5\cdot5\cdot5\cdot5\cdot5\cdot5}=\dfrac1{5\cdot5\cdot5\cdot5}=(5^4)^{-1}=5^{-4}$, o bien $5^4 \div 5^8 = 5^{4-8}=5^{-4}$ \\ <br />6. Multiplicaci\'on de potencias de igual exponente: $$a^n \cdot b^n=(a \cdot b)^n, \forall a,b\in\mathbb{R}, n\in\mathbb{Z}$$ Demostraci\'on: $$a^n \cdot b^n = \underbrace{a \cdots a}_{n \text{ veces } a} \cdot \underbrace{b\cdots b}_{n \text{ veces } b}= \underbrace{(a \cdot b) \cdot (a \cdot b) \cdots (a \cdot b)}_{n \text{ veces}}=(a \cdot b)^n$$$ Saludos Mensaje modificado por p.j.t el Jan 12 2008, 08:15 PM -------------------- asdf

Uchiha Sasuke Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 9 2008, 12:14 AM Publicado: #2
Dios Matemático Grupo: Usuario FMAT Mensajes: 391 Registrado: 9-January 08 Desde: Clan uchiha...xd Miembro Nº: 14.464 Nacionalidad: Sexo:	Te propongo uno de potencias para poner en practica lo expuesto : cual de las siguientes alternativas es el resultado de reducir al maximo la expresion : $TEX: \[<br />6^{n - 2} \cdot3^{n + 2} \cdot2^3 <br />\]$ a) $TEX: \[<br />9^n <br />\]$ b)18 c) $TEX: \[<br />18^n <br />\]$ d) $TEX: \[<br />36^n <br />\]$ e) $TEX: \[<br />63^n <br />\]$ --------------------

DoomH~ Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 14 2008, 05:27 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987	Esta es una pequeña guia de potencias, bueno, en realidad es una parte porque es algo extensa pero buena , interesante y entretenida. Saludos PD:Las otras partes vienen en otros post. Mensaje modificado por 69___ el Jan 14 2008, 05:59 PM Archivo(s) Adjunto(s) Potencias.PNG ( 239.06k ) Número de descargas: 42 -------------------- CHAO.

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 2 2008, 12:54 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	Para los que quieran la resolucion de los problemas de 69__: Item I $TEX: <br />\[<br />\begin{gathered}<br />\noindent \left.1 \right) (-1)^4=1 \hfill \\<br />\left.2 \right) \left( \dfrac32 \right)^2=\dfrac{3^2}{2^2}=\dfrac94 \hfill \\<br />\left.3 \right) \left(-\dfrac15 \right)^4= \left(-1 \times \dfrac15 \right)^4=\left(-1 \right)^4 \times \dfrac{1^4}{5^4}=\dfrac1{625} \hfill \\<br />\left.4\right) \left(0,25 \right)^2=\left( \dfrac14 \right)^2 = \dfrac{1^2}{4^2}=\dfrac1{16} \hfill \\<br />\left.5 \right) \left(\dfrac23 \right)^3=\dfrac{2^3}{3^3}=\dfrac8{27} \hfill \\<br />\left.6 \right) \left( \dfrac{-1}5 \right)^2=\dfrac{\left(-1\right)^2}{5^2}=\dfrac1{25} \hfill \\<br />\left.7 \right) \left( \dfrac{-3}4 \right)^2= \dfrac{\left(-3\right)^2}{4^2}=\dfrac9{16} \hfill \\<br />\left.8 \right) \left( -0,125 \right)^2= \left( \dfrac{-1}8 \right)^2=\dfrac{\left(-1\right)^2}{8^2}=\dfrac1{64} \hfill \\<br />\left.9 \right) \left( 0,\overline{3} \right)^2= \left( \dfrac13 \right)^2= \dfrac{1^2}{3^2}=\dfrac19 \hfill \\<br />\left.{10} \right) \left(\dfrac{-2}3\right)^5=\dfrac{\left(-2\right)^5}{3^5}=-\dfrac{32}{243} \hfill<br />\end{gathered}<br />\]<br />$ Item II $TEX: <br />\[<br />\begin{gathered}<br />\left.1 \right) \left(\dfrac12\right)^2 \times \left(\dfrac12\right)^3= \left(\dfrac12\right)^{3+2}= \left( \dfrac12 \right)^5= \dfrac{1^5}{2^5}=\dfrac1{32} \hfill \\<br />\left.2 \right) \left(\dfrac{-2}5\right)^4 \times \left(\dfrac{-2}5\right)^1 \times \left(\dfrac{-2}5\right)^{-2}= \left(\dfrac{-2}5\right)^{4+1+\left(-2\right)}= \left(\dfrac{-2}5\right)^3= \dfrac{\left(-2\right)^3}{5^3}=\dfrac{-8}{625} \hfill \\<br />\left.3 \right) \left(\dfrac47\right)^{-3} \times \left(\dfrac47\right)^{5} \times \left(\dfrac47\right)^1 \times \left(\dfrac47\right)^2= \left(\dfrac47\right)^{\left(-3\right)+5+1+2}=\left(\dfrac47\right)^{5}=\dfrac{4^5}{7^5}=\dfrac{1024}{16807} \hfill \\<br />\left.4 \right) \left(0,34\right)^1 \times \left(0,34\right)^2=\left(0,34\right)^3 \hfill \\<br />\left.5 \right) \left(\dfrac{-3}8\right)^3 \times \left(\dfrac{-3}8\right)^{-2} \times \left(\dfrac{-3}8\right)^1= \left(\dfrac{-3}8\right)^{3+\left(-2\right)+1}=\left(\dfrac{-3}8\right)^2=\dfrac{\left(-3\right)^2}{8^2}=\dfrac9{64} \hfill \\<br />\left.6 \right) \left(0,\overline{3}\right)^2 \times \left(\dfrac13\right)^{-1}=\left(\dfrac13\right)^2 \times \left(\dfrac13\right)^{-1}= \left(\dfrac13\right)^{2+\left(-1\right)}=\dfrac13 \hfill<br />\end{gathered}<br />\]<br />$ Cualquier falla me avisan Saludos PD: Uchiha sasuke, estas seguro que esas son las alternativas?. Porque me dio 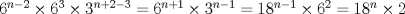$TEX: $6^{n-2}\times 6^3 \times 3^{n+2-3}=6^{n+1}\times 3^{n-1}=18^{n-1} \times 6^2 = 18^n \times 2$$ -------------------- asdf

DoomH~ Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 2 2008, 01:14 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987	No hay fallas p.j.t , esta correcto Felicitaciones. Saludos -------------------- CHAO.

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 2 2008, 11:34 PM Publicado: #6
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(69___ @ Feb 2 2008, 06:10 PM) No hay fallas p.j.t , esta correcto Felicitaciones. Saludos Si tienes razon , ese ejercicio lo recordaba , es uno del texto CEPECH y el ejercicio es asi: $TEX: \[<br />6^{n - 2} \bullet 3^{n + 2} \bullet 2^2 <br />\]$ entonces ahi se puede hacr y obtener un resultado acorde con las alternativas : $TEX: \[<br />\begin{gathered}<br /> 6^{n - 2} \bullet 3^{n + 2} \bullet 2^2 \hfill \\<br /> 6^n \bullet 6^{ - 2} \bullet 3^n \bullet 3^2 \bullet 2^2 \hfill \\<br /> 6^n \bullet 3^n \bullet 3^2 \bullet 2^2 \bullet 6^{ - 2} \hfill \\<br /> 18^n \bullet 6^2 \bullet 6^{ - 2} \hfill \\<br /> \therefore 18^n \hfill \\ <br />\end{gathered} <br />\]$ Alternativa C Saludos -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Uchiha Sasuke Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 18 2008, 03:18 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 391 Registrado: 9-January 08 Desde: Clan uchiha...xd Miembro Nº: 14.464 Nacionalidad: Sexo:	CITA(Uchiha Sasuke @ Jan 9 2008, 05:10 AM) Te propongo uno de potencias para poner en practica lo expuesto : cual de las siguientes alternativas es el resultado de reducir al maximo la expresion : $TEX: \[<br />6^{n - 2} \cdot3^{n + 2} \cdot2^3 <br />\]$ a) $TEX: \[<br />9^n <br />\]$ b)18 c) $TEX: \[<br />18^n <br />\]$ d) $TEX: \[<br />36^n <br />\]$ e) $TEX: \[<br />63^n <br />\]$ disculpa por las molestias salu2 --------------------

Panxoss Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 11 2008, 03:56 PM Publicado: #8
Maestro Matemático Grupo: Usuario FMAT Mensajes: 107 Registrado: 6-February 08 Miembro Nº: 15.305 Nacionalidad: Colegio/Liceo: Sexo:	nunca esta demas...gracias --------------------

†Sasuke† Ver Perfil del Miembro Ver los mensajes de este miembro	Mar 15 2008, 11:41 PM Publicado: #9
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 21 Registrado: 20-April 07 Desde: santiago Miembro Nº: 5.344 Nacionalidad: Colegio/Liceo: Sexo:	por eso no m daba el resultado

DoomH~ Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 20 2008, 01:17 PM Publicado: #10
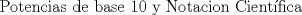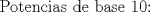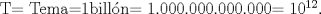Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.429 Registrado: 6-October 07 Miembro Nº: 10.987	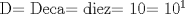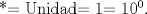$TEX: Potencias de base 10 y Notacion Científica$ $TEX: Potencias de base 10:$ $TEX: T= Tema=1billón= 1.000.000.000.000= $10^{12}$.$ $TEX: G= Giga= 1.000 millones= 1.000.000.000= $10^{9}$.$ $TEX: M= Mega= 1 millón= 1.000.000= $10^{6}$.$ $TEX: K= Kilo= mil= 1.000 =$10^{3}$.$ $TEX: H= Hecto= cien= 100=$10^{2}$.$ $TEX: D= Deca= diez= 10= $10^{1}$$ $TEX: *= Unidad= 1= $10^{0}$.$ Continuara... PD: En un ratito mas termino...falta arto aun. -------------------- CHAO.

« Posterior · Contenidos 8º Básico · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 04:59 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.