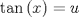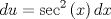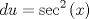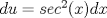Propuesto 95 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Consultas > Banco de Problemas Resueltos > Cálculo > Integrales

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Propuesto 95, Regalo del chef

Jean Renard Gran... Jean Renard Granier Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 6 2008, 03:28 PM Publicado: #1
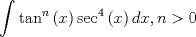
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad: Universidad: Sexo:	Evaluar $TEX: $$\int {\tan ^n } \left( x \right)\sec ^4 \left( x \right)dx,n > 0$$$ Mensaje modificado por Krizalid el Mar 9 2008, 09:01 PM -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:11 PM Publicado: #2
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Uchiha Itachi @ Jan 9 2008, 01:04 AM) Aca voy con mi desarrollo : ^^ $TEX: \[<br />\begin{gathered}<br /> \int {tg^n \alpha \sec ^4 \alpha d\alpha = \int {(\sec ^2 \alpha - 1)^n } } (\sec ^4 )d\alpha \hfill \\<br /> u = \sec ^2 \alpha - 1 \Rightarrow du = 2\sec ^2 \alpha tg\alpha \to du = 2(u - 1)\sqrt u \hfill \\<br /> 2\int {u^n (u + 1)^2 (u - 1)\sqrt u } du = 2\int {u^{\frac{{2n + 1}}<br />{2}} } (u^3 + u^2 - u - 1)du \hfill \\<br /> 2\left[ {\int {u^{\frac{{2n + 7}}<br />{2}} + \int {u^{\frac{{2n + 5}}<br />{2}} } - \int {u^{n + 1} - \int {u^{\frac{{2n + 1}}<br />{2}} } } } } \right] \hfill \\<br /> \therefore I = \frac{{4u^{\frac{{2n + 9}}<br />{2}} }}<br />{{2n + 9}} + \frac{{4u^{\frac{{2n + 7}}<br />{2}} }}<br />{{2n + 7}} - \frac{{2u^{n + 2} }}<br />{{n + 2}} - \frac{{2u^{\frac{{2n + 3}}<br />{2}} }}<br />{{2n + 3}} \hfill \\ <br />\end{gathered} <br />\]$ falta cambiar la variable , pero esta listo ^^ que es : $TEX: \[<br />u = \sec ^2 \alpha - 1<br />\]$ jaja xuta la embarre al principio estoy editando , deberia ser asi . $TEX: \[<br />\sec ^2 \alpha = u + 1<br />\]$ ( cuando reemplaze el du ) Mensaje modificado por Uchiha Itachi el Jan 8 2008, 08:12 PM -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Jean Renard Gran... Jean Renard Granier Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:15 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad: Universidad: Sexo:	CITA(Uchiha Itachi @ Jan 8 2008, 11:04 PM) Aca voy con mi desarrollo : ^^ $TEX: \[<br />\begin{gathered}<br /> \int {tg^n \alpha \sec ^4 \alpha d\alpha = \int {(\sec ^2 \alpha - 1)^n } } (\sec ^4 )d\alpha \hfill \\<br /> u = \sec ^2 \alpha - 1 \Rightarrow du = 2\sec ^2 \alpha tg\alpha \to du = 2(u - 1)\sqrt u \hfill \\<br /> 2\int {u^n (u + 1)^2 (u - 1)\sqrt u } du = 2\int {u^{\frac{{2n + 1}}<br />{2}} } (u^3 + u^2 - u - 1)du \hfill \\<br /> 2\left[ {\int {u^{\frac{{2n + 7}}<br />{2}} + \int {u^{\frac{{2n + 5}}<br />{2}} } - \int {u^{n + 1} - \int {u^{\frac{{2n + 1}}<br />{2}} } } } } \right] \hfill \\<br /> \therefore I = \frac{{4u^{\frac{{2n + 9}}<br />{2}} }}<br />{{2n + 9}} + \frac{{4u^{\frac{{2n + 7}}<br />{2}} }}<br />{{2n + 7}} - \frac{{2u^{n + 2} }}<br />{{n + 2}} - \frac{{2u^{\frac{{2n + 3}}<br />{2}} }}<br />{{2n + 3}} \hfill \\ <br />\end{gathered} <br />\]$ falta cambiar la variable , pero esta listo ^^ que es : $TEX: \[<br />u = \sec ^2 \alpha - 1<br />\]$ La respuesta es incorrecta, con ese cambio de variable el desarrollo va para otro lado. Te recomiendo hacer de nuevo la integral con el siguiente cambo de variable $TEX: $$\tan \left( x \right) = u$$$ Inténtalo de nuevo. Saludos -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:19 PM Publicado: #4
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> 2\int {u^n (u + 1)^3 } \sqrt u du = 2\int {u^n } (u^3 + 3u^2 + 3u + 1)\sqrt u du \hfill \\<br /> 2\int {u^{\frac{{2n + 1}}<br />{2}} } (u^3 + 3u^2 + 3u + 1)du = 2\left[ {\int {u^{\frac{{2n + 7}}<br />{2}} } + 3\int {u^{\frac{{2n + 5}}<br />{2}} } + 3\int {u^{\frac{{2n + 3}}<br />{2}} } + \int {u^{\frac{{2n + 1}}<br />{2}} } } \right] \hfill \\<br /> \therefore 2\left[ {\frac{{2u^{2n + 11} }}<br />{{2n + 11}} + \frac{{6u^{\frac{{2n + 9}}<br />{2}} }}<br />{{2n + 9}} + \frac{{6u^{\frac{{2n + 7}}<br />{2}} }}<br />{{2n + 7}} + \frac{{2u^{\frac{{2n + 5}}<br />{2}} }}<br />{{2n + 5}}} \right] \hfill \\ <br />\end{gathered} <br />\]$ espero ahora este bien ^^ ( lei lo de arriba , lo are con ese cambio de variable ^^ , gracias , saludos ) Mensaje modificado por Uchiha Itachi el Jan 8 2008, 08:20 PM -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:27 PM Publicado: #5
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Nota : me equivoque muy tonto con el cambio de variable ... Haciendolo ... Con errores uno aprende , puxas que me equivoco en tonteras , gracias , saludos . Respuesta : $TEX: \[<br />\begin{gathered}<br /> u = tg(x) \to du = \sec ^2 (x)dx \Rightarrow \frac{{du}}<br />{{\sec ^2 (x)}} = dx \hfill \\<br /> \sec (x) = \sqrt {u^2 + 1} \Rightarrow dx = \frac{{du}}<br />{{u^2 + 1}} \hfill \\<br /> \int {\frac{{u^n (u^2 + 1)^2 }}<br />{{u^2 + 1}}} = \int {u^n (u^2 + 1)} du \hfill \\<br /> \int {u^{n + 2} du + \int {u^n } } du = \frac{{u^{n + 3} }}<br />{{n + 3}} + \frac{{u^{n + 1} }}<br />{{n + 1}} \hfill \\<br /> \therefore I = \frac{{tg^{n + 3} (x)}}<br />{{n + 3}} + \frac{{tg^{n + 1} (x)}}<br />{{n + 1}} + c \hfill \\ <br />\end{gathered} <br />\]$ Mensaje modificado por Uchiha Itachi el Jan 8 2008, 08:51 PM -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

Jean Renard Gran... Jean Renard Granier Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:45 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad: Universidad: Sexo:	Ojo, $TEX: $$du = \sec ^2 \left( x \right)dx$$$ No hay problema, recuerda que reforzando se supera. Saludos P.D Gracias por la observación Xapi. Mensaje modificado por neo shykerex el Jan 8 2008, 09:01 PM -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:58 PM Publicado: #7
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(neo shykerex @ Jan 9 2008, 01:45 AM) Ojo, $TEX: $$du = \sec ^2 \left( x \right)$$$ No hay problema, recuerda que reforzando se supera. Saludos Hola si tienes razon , con esfuerzo uno se supera , ademas que las mates son mucha practica , quiero mejorar en las integrales y se que aki puedo lograrlo , gracias y saludos . $TEX: \[<br />\begin{gathered}<br /> u = tg(x) \to du = \sec ^2 (x)dx \Rightarrow \frac{{du}}<br />{{\sec ^2 (x)}} = dx \hfill \\<br /> \sec (x) = \sqrt {u^2 + 1} \Rightarrow dx = \frac{{du}}<br />{{u^2 + 1}} \hfill \\<br /> \int {\frac{{u^n (u^2 + 1)^2 }}<br />{{u^2 + 1}}} = \int {u^n (u^2 + 1)} du \hfill \\<br /> \int {u^{n + 2} du + \int {u^n } } du = \frac{{u^{n + 3} }}<br />{{n + 3}} + \frac{{u^{n + 1} }}<br />{{n + 1}} \hfill \\<br /> \therefore I = \frac{{tg^{n + 3} (x)}}<br />{{n + 3}} + \frac{{tg^{n + 1} (x)}}<br />{{n + 1}} + c \hfill \\ <br />\end{gathered} <br />\]$ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

XaPi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 08:58 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.872 Registrado: 9-March 06 Desde: Welcome Miembro Nº: 614 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(neo shykerex @ Jan 8 2008, 11:45 PM) Ojo, $TEX: $$du = \sec ^2 \left( x \right)$$$ Ojo $TEX: $du = sec^2(x) dx$$ Saludos -------------------- USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan ----------------- CURRICULUM VITAE ----------------- 296 pts en la PSU de Matemáticas Admisión 2010. Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica U. de Talca VII Region Chile

Jean Renard Gran... Jean Renard Granier Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 09:03 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.920 Registrado: 19-August 06 Desde: DIM, DCC Beauchef Miembro Nº: 1.989 Nacionalidad: Universidad: Sexo:	CITA(Uchiha Itachi @ Jan 8 2008, 11:58 PM) Hola si tienes razon , con esfuerzo uno se supera , ademas que las mates son mucha practica , quiero mejorar en las integrales y se que aki puedo lograrlo , gracias y saludos . $TEX: \[<br />\begin{gathered}<br /> u = tg(x) \to du = \sec ^2 (x)dx \Rightarrow \frac{{du}}<br />{{\sec ^2 (x)}} = dx \hfill \\<br /> \sec (x) = \sqrt {u^2 + 1} \Rightarrow dx = \frac{{du}}<br />{{u^2 + 1}} \hfill \\<br /> \int {\frac{{u^n (u^2 + 1)^2 }}<br />{{u^2 + 1}}} = \int {u^n (u^2 + 1)} du \hfill \\<br /> \int {u^{n + 2} du + \int {u^n } } du = \frac{{u^{n + 3} }}<br />{{n + 3}} + \frac{{u^{n + 1} }}<br />{{n + 1}} \hfill \\<br /> \therefore I = \frac{{tg^{n + 3} (x)}}<br />{{n + 3}} + \frac{{tg^{n + 1} (x)}}<br />{{n + 1}} + c \hfill \\ <br />\end{gathered} <br />\]$ Ahora sí, respuesta correcta. Aplicando Sharingan, fíjate en lo siguiente. 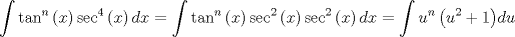$TEX: $$\int {\tan ^n \left( x \right)} \sec ^4 \left( x \right)dx = \int {\tan ^n \left( x \right)} \sec ^2 \left( x \right)\sec ^2 \left( x \right)dx = \int {u^n \left( {u^2 + 1} \right)} du$$$ $TEX: $$\sec ^2 \left( x \right)dx = du,u^2 + 1 = \tan ^2 \left( x \right) + 1 = \sec ^2 \left( x \right)$$$ A eso iba mi comentario, el segundo cambio de variable está incorrecto por un detalle mínimo al aplicar Regla de la Cadena. Aplicando lo que he puesto, terminamos totalmente. De todas formas, felicitaciones. La famosa alineación, se me había olvidado. Mala costumbre, a partir de ahora la aplico. Sorry, no he tenido un día muy bueno que digamos. Mensaje modificado por neo shykerex el Jan 8 2008, 10:37 PM -------------------- Miembro de Anime No Seishin Doukokai, podrías ser el próximo.

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 8 2008, 10:22 PM Publicado: #10
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(neo shykerex @ Jan 9 2008, 02:03 AM) Ahora sí, respuesta correcta. Aplicando Sharingan, fíjate en lo siguiente. 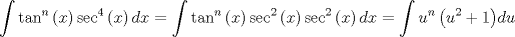$TEX: $$\int {\tan ^n \left( x \right)} \sec ^4 \left( x \right)dx = \int {\tan ^n \left( x \right)} \sec ^2 \left( x \right)\sec ^2 \left( x \right)dx = \int {u^n \left( {u^2 + 1} \right)} du$$$ $TEX: $$\sec ^2 \left( x \right)dx = du,u^2 + 1 = \tan ^2 \left( x \right) + 1 = \sec ^2 \left( x \right)$$$ A eso iba mi comentario, el segundo cambio de variable está incorrecto por un detalle mínimo al aplicar Regla de la Cadena. Aplicando lo que he puesto, terminamos totalmente. De todas formas, felicitaciones. AAA de veras tienes razon , hice un paso innecesario , jaja " ocupando mi sharingan " que wena , muchas gracias neo shykerex , saludos . ^^ Por la cresta, ¿cómo hago para que salga todo en una línea?, ¿se puede reducir el tamaño en ese caso?. AAA de veras tienes razon , hice un paso innecesario , jaja " ocupando mi sharingan " que wena , muchas gracias neo shykerex , saludos . ^^ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

« Posterior · Integrales · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 24th November 2024 - 03:54 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.