C2 Lic. en Matemática - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

C2 Lic. en Matemática, MAT1305 - 1S, 2007

Opciones

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 3 2008, 02:07 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \begin{enumerate}\item Demuestre que en todo tri\'angulo ABC se cumple que: <br />$\dfrac{1}{h_a}+\dfrac{1}{h_b}+\dfrac{1}{h_c}=\dfrac{1}{\rho}$. \item\begin{enumerate} <br />Resuelva la ecuaci\'on: $Arccos(x) - Arcsen(x) = Arccos(x\sqrt{3}) .$ <br />\end{enumerate}\item Resuelva la ecuaci\'on: <br />$\operatorname{sen} 5\theta - \operatorname{sen} 3\theta <br />= \sqrt{2}\cos 4\theta .$\end{enumerate}$ PD: Para el primer ejercicio, h corresponde a la altura (asociada al lado correspondiente) del triángulo ABC, y rho simboliza el radio de la circunferencia inscrita a él. Mensaje modificado por Pily el Jan 3 2008, 02:20 PM --------------------

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 3 2008, 10:01 PM Publicado: #2
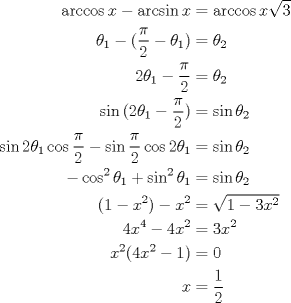
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	No sé si ta bn, pq no sé trabajar mucho con ecuaciones trigonométricas pero al menos el resultado tiene sentido D: ! $TEX: \begin{equation}\begin{aligned}<br />\arccos{x} - \arcsin{x} &= \arccos{x\sqrt{3}}\\<br />\theta_1 - (\dfrac{\pi}{2} - \theta_1) &= \theta_2\\<br />2\theta_1 - \dfrac{\pi}{2} &= \theta_2\\<br />\sin{(2\theta_1-\dfrac{\pi}{2})} &= \sin{\theta_2}\\<br />\sin{2\theta_1}\cos{\dfrac{\pi}{2}}-\sin{\dfrac{\pi}{2}}\cos{2\theta_1} &= \sin{\theta_2}\\<br />-\cos^2{\theta_1}+\sin^2{\theta_1} &= \sin{\theta_2}\\<br />(1-x^2) - x^2 &= \sqrt{1-3x^2}\\<br />4x^4 - 4x^2 &= 3x^2\\<br />x^2(4x^2-1) &= 0\\<br />x &= \dfrac{1}{2}\\<br />\end{aligned}\end{equation}$ Mensaje modificado por Abu-Khalil el Jan 4 2008, 08:45 PM -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 04:12 PM Publicado: #3
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Pily @ Jan 3 2008, 05:07 PM) $TEX: <br />% MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaci4CaiaacM<br />% gacaGGUbGaaGynaiabeI7aXjabgkHiTiGacohacaGGPbGaaiOBaiaa<br />% iodacqaH4oqCcqGH9aqpdaGcaaqaaiaaikdaaSqabaGcciGGJbGaai<br />% 4BaiaacohacaaI0aGaeqiUdehaaa!48A0!<br />\[<br />\sin 5\theta - \sin 3\theta = \sqrt 2 \cos 4\theta <br />\]<br />$ $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGJb<br />% Gaae4Baiaab6gacaqGVbGaae4yaiaabMgacaqGLbGaaeOBaiaabsga<br />% caqGVbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqGVbGaaeOCai<br />% aab2gacaqG1bGaaeiBaiaabggacaqG6aaabaaabaGaae4CaiaabMga<br />% caqGUbGaaeyqaiaab2cacaqGZbGaaeyAaiaab6gacaqGcbGaaeypai<br />% aabkdacaqGZbGaaeyAaiaab6gadaqadaqaamaalaaabaGaaeyqaiaa<br />% b2cacaqGcbaabaGaaeOmaaaaaiaawIcacaGLPaaacqGHflY1ciGGJb<br />% Gaai4BaiaacohadaqadaqaamaalaaabaGaamyqaiabgUcaRiaadkea<br />% aeaacaaIYaaaaaGaayjkaiaawMcaaaqaaaqaaiaabchacaqGHbGaae<br />% OCaiaabggacaqGGaGaaeOzaiaabggacaqGJbGaaeyAaiaabYgacaqG<br />% PbGaaeizaiaabggacaqGKbGaaeiiaiaabsgacaqGLbGaaeiiaiaabw<br />% gacaqGZbGaae4yaiaabkhacaqGPbGaaeiDaiaabwhacaqGYbGaaeyy<br />% aiaabccacaqGLbGaaeOBaiaabccacaqGTbGaaeyyaiaabshacaqGOb<br />% GaaeiDaiaabMhacaqGWbGaaeyzaiaabccacaqG4bGaaeypaiabeI7a<br />% XbqaaaqaaiGacohacaGGPbGaaiOBaiaaiwdacaWG4bGaeyOeI0Iaci<br />% 4CaiaacMgacaGGUbGaaG4maiaadIhacqGH9aqpdaGcaaqaaiaaikda<br />% aSqabaGcciGGJbGaai4BaiaacohacaaI0aGaamiEaaqaaaqaaiaaik<br />% daciGGZbGaaiyAaiaac6gadaqadaqaamaalaaabaGaaGynaiaadIha<br />% cqGHsislcaaIZaGaamiEaaqaaiaaikdaaaaacaGLOaGaayzkaaGaey<br />% yXICTaci4yaiaac+gacaGGZbWaaeWaaeaadaWcaaqaaiaaiwdacaWG<br />% 4bGaey4kaSIaaG4maiaadIhaaeaacaaIYaaaaaGaayjkaiaawMcaai<br />% abg2da9maakaaabaGaaGOmaaWcbeaakiGacogacaGGVbGaai4Caiaa<br />% isdacaWG4baabaaabaGaaGOmaiGacohacaGGPbGaaiOBaiaadIhacq<br />% GHflY1ciGGJbGaai4BaiaacohacaaI0aGaamiEaiabg2da9maakaaa<br />% baGaaGOmaaWcbeaakiGacogacaGGVbGaai4CaiaaisdacaWG4baaba<br />% aabaGaci4CaiaacMgacaGGUbGaamiEaiabg2da9maalaaabaWaaOaa<br />% aeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaeaaaeaadaqjEaqaaiaadI<br />% hacqGH9aqpcaaI0aGaaGynaaaaaaaa!D428!<br />\[<br />\begin{gathered}<br /> {\text{conociendo la formula:}} \hfill \\<br /> \hfill \\<br /> {\text{sinA - sinB = 2sin}}\left( {\frac{{{\text{A - B}}}}<br />{{\text{2}}}} \right) \cdot \cos \left( {\frac{{A + B}}<br />{2}} \right) \hfill \\<br /> \hfill \\<br /> {\text{para facilidad de escritura en mathtype x = }}\theta \hfill \\<br /> \hfill \\<br /> \sin 5x - \sin 3x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin \left( {\frac{{5x - 3x}}<br />{2}} \right) \cdot \cos \left( {\frac{{5x + 3x}}<br />{2}} \right) = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin x \cdot \cos 4x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> \sin x = \frac{{\sqrt 2 }}<br />{2} \hfill \\<br /> \hfill \\<br /> \boxed{x = 45} \hfill \\ <br />\end{gathered} <br />\]<br />$ saludos editado: con respeto a la 1 se podria decir que p (rho) es circunradio? Mensaje modificado por naxoobkn el Jan 31 2008, 04:29 PM -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 05:25 PM Publicado: #4
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(naxoobkn @ Jan 31 2008, 06:12 PM) $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGJb<br />% Gaae4Baiaab6gacaqGVbGaae4yaiaabMgacaqGLbGaaeOBaiaabsga<br />% caqGVbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqGVbGaaeOCai<br />% aab2gacaqG1bGaaeiBaiaabggacaqG6aaabaaabaGaae4CaiaabMga<br />% caqGUbGaaeyqaiaab2cacaqGZbGaaeyAaiaab6gacaqGcbGaaeypai<br />% aabkdacaqGZbGaaeyAaiaab6gadaqadaqaamaalaaabaGaaeyqaiaa<br />% b2cacaqGcbaabaGaaeOmaaaaaiaawIcacaGLPaaacqGHflY1ciGGJb<br />% Gaai4BaiaacohadaqadaqaamaalaaabaGaamyqaiabgUcaRiaadkea<br />% aeaacaaIYaaaaaGaayjkaiaawMcaaaqaaaqaaiaabchacaqGHbGaae<br />% OCaiaabggacaqGGaGaaeOzaiaabggacaqGJbGaaeyAaiaabYgacaqG<br />% PbGaaeizaiaabggacaqGKbGaaeiiaiaabsgacaqGLbGaaeiiaiaabw<br />% gacaqGZbGaae4yaiaabkhacaqGPbGaaeiDaiaabwhacaqGYbGaaeyy<br />% aiaabccacaqGLbGaaeOBaiaabccacaqGTbGaaeyyaiaabshacaqGOb<br />% GaaeiDaiaabMhacaqGWbGaaeyzaiaabccacaqG4bGaaeypaiabeI7a<br />% XbqaaaqaaiGacohacaGGPbGaaiOBaiaaiwdacaWG4bGaeyOeI0Iaci<br />% 4CaiaacMgacaGGUbGaaG4maiaadIhacqGH9aqpdaGcaaqaaiaaikda<br />% aSqabaGcciGGJbGaai4BaiaacohacaaI0aGaamiEaaqaaaqaaiaaik<br />% daciGGZbGaaiyAaiaac6gadaqadaqaamaalaaabaGaaGynaiaadIha<br />% cqGHsislcaaIZaGaamiEaaqaaiaaikdaaaaacaGLOaGaayzkaaGaey<br />% yXICTaci4yaiaac+gacaGGZbWaaeWaaeaadaWcaaqaaiaaiwdacaWG<br />% 4bGaey4kaSIaaG4maiaadIhaaeaacaaIYaaaaaGaayjkaiaawMcaai<br />% abg2da9maakaaabaGaaGOmaaWcbeaakiGacogacaGGVbGaai4Caiaa<br />% isdacaWG4baabaaabaGaaGOmaiGacohacaGGPbGaaiOBaiaadIhacq<br />% GHflY1ciGGJbGaai4BaiaacohacaaI0aGaamiEaiabg2da9maakaaa<br />% baGaaGOmaaWcbeaakiGacogacaGGVbGaai4CaiaaisdacaWG4baaba<br />% aabaGaci4CaiaacMgacaGGUbGaamiEaiabg2da9maalaaabaWaaOaa<br />% aeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaeaaaeaadaqjEaqaaiaadI<br />% hacqGH9aqpcaaI0aGaaGynaaaaaaaa!D428!<br />\[<br />\begin{gathered}<br /> {\text{conociendo la formula:}} \hfill \\<br /> \hfill \\<br /> {\text{sinA - sinB = 2sin}}\left( {\frac{{{\text{A - B}}}}<br />{{\text{2}}}} \right) \cdot \cos \left( {\frac{{A + B}}<br />{2}} \right) \hfill \\<br /> \hfill \\<br /> {\text{para facilidad de escritura en mathtype x = }}\theta \hfill \\<br /> \hfill \\<br /> \sin 5x - \sin 3x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin \left( {\frac{{5x - 3x}}<br />{2}} \right) \cdot \cos \left( {\frac{{5x + 3x}}<br />{2}} \right) = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin x \cdot \cos 4x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> \sin x = \frac{{\sqrt 2 }}<br />{2} \hfill \\<br /> \hfill \\<br /> \boxed{x = 45} \hfill \\ <br />\end{gathered} <br />\]<br />$ saludos editado: con respeto a la 1 se podria decir que p (rho) es circunradio? En la primera, $TEX: ${\color{red}\rho}$$ corresponde al radio de la circunferencia inscrita (inradio). Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 08:05 PM Publicado: #5
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Rurouni Kenshin @ Jan 31 2008, 08:25 PM) En la primera, $TEX: ${\color{red}\rho}$$ corresponde al radio de la circunferencia inscrita (inradio). Saludos gracias, si es asi entonces pude demostrar esa igualdad $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjua<br />% qaaiaadcfacaGGUaGaamiraiaac6cacaWGrbaaaaqaaaqaamaalaaa<br />% baGaaGymaaqaaiaadIgacaWGHbaaaiabgUcaRmaalaaabaGaaGymaa<br />% qaaiaadIgacaWGIbaaaiabgUcaRmaalaaabaGaaGymaaqaaiaadIga<br />% caWGJbaaaiabg2da9maalaaabaGaaGymaaqaaiabeg8aYbaaaeaaae<br />% aacaqG0bGaaeyzaiaab6gacaqGLbGaaeyBaiaab+gacaqGZbGaaeii<br />% aiaabghacaqG1bGaaeyzaiaabccacaqGZbGaaeyyaiaabkgacaqGLb<br />% GaaeOCaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeiBaiaabgga<br />% caqGGaGaaeyyaiaabYgacaqG0bGaaeyDaiaabkhacaqGHbGaaeiiai<br />% aabohacaqGLbGaaeiiaiaabchacaqG1bGaaeyzaiaabsgacaqGLbGa<br />% aeiiaiaabwgacaqGUbGaae4yaiaab+gacaqGUbGaaeiDaiaabkhaca<br />% qGHbGaaeOCaiaabccacaqGLbGaaeOBaiaabccacaqGMbGaaeyDaiaa<br />% b6gacaqGJbGaaeyAaiaab+gacaqGUbGaaeiiaiaabsgacaqGLbGaae<br />% iiaiaabYgacaqGVbGaae4CaiaabccacaqGSbGaaeyyaiaabsgacaqG<br />% VbGaae4CaaqaaaqaaiaadohacaWGLbGaamyyaiaacQdacaWGibGaey<br />% ypa0ZaaOaaaeaacaWGZbGaaiikaiaadohacqGHsislcaWGHbGaaiyk<br />% aiaacIcacaWGZbGaeyOeI0IaamOyaiaacMcacaGGOaGaam4Caiabgk<br />% HiTiaadogacaGGPaaaleqaaaGcbaaabaWaaSaaaeaacaaIXaaabaWa<br />% aSaaaeaacaaIYaGaamisaaqaaiaadggaaaaaaiabgUcaRmaalaaaba<br />% GaaGymaaqaamaalaaabaGaaGOmaiaadIeaaeaacaWGIbaaaaaacqGH<br />% RaWkdaWcaaqaaiaaigdaaeaadaWcaaqaaiaaikdacaWGibaabaGaam<br />% 4yaaaaaaGaeyypa0ZaaSaaaeaacaWGHbaabaGaaGOmaiaadIeaaaGa<br />% ey4kaSYaaSaaaeaacaWGIbaabaGaaGOmaiaadIeaaaGaey4kaSYaaS<br />% aaaeaacaWGJbaabaGaaGOmaiaadIeaaaGaeyypa0ZaaSaaaeaacaaI<br />% XaaabaGaaGOmaiaadIeaaaGaaiikaiaadggacqGHRaWkcaWGIbGaey<br />% 4kaSIaam4yaiaacMcaaeaaaeaacaqGWbGaaeyzaiaabkhacaqGVbGa<br />% aeiiaiaabogacaqGVbGaaeyBaiaab+gacaqGGaGaaeisaiaabccaca<br />% qGLbGaae4CaiaabccacaqGLbGaaeiBaiaabccacaqGHbGaaeOCaiaa<br />% bwgacaqGHbGaaeiiaiaabsgacaqGLbGaaeiiaiaabwgacaqGSbGaae<br />% iiaiaabsgacaqGLbGaaeiBaiaabccacaqG0bGaaeOCaiaabMgacaqG<br />% HbGaaeOBaiaabEgacaqG1bGaaeiBaiaab+gacaqGSaGaaeiiaiaabY<br />% gacaqGHbGaaeiiaiaabogacaqG1bGaaeyyaiaabYgacaqGGaGaaeiD<br />% aiaabggacaqGTbGaaeOyaiaabMgacaqGLbGaaeOBaiaabccacaqGWb<br />% GaaeyDaiaabwgacaqGKbGaaeyzaiaabccacaqGZbGaaeyzaiaabkha<br />% caqGGaGaaeyzaiaabIhacaqGWbGaaeOCaiaabwgacaqGZbGaaeyyai<br />% aabsgacaqGHbaabaGaae4yaiaab+gacaqGUbGaaeiiaiaabYgacaqG<br />% HbGaaeiiaiaabohacaqGPbGaae4zaiaabwhacaqGPbGaaeyzaiaab6<br />% gacaqG0bGaaeyzaiaabccacaqGMbGaae4BaiaabkhacaqGTbGaaeyD<br />% aiaabYgacaqGHbaabaaabaGaamyyaiaadkhacaWGLbGaamyyaiablo<br />% Bjwjabg2da9maakaaabaGaam4CaiaacIcacaWGZbGaeyOeI0Iaamyy<br />% aiaacMcacaGGOaGaam4CaiabgkHiTiaadkgacaGGPaGaaiikaiaado<br />% hacqGHsislcaWGJbGaaiykaaWcbeaakiabg2da9maalaaabaGaeqyW<br />% diNaaeikaiaabggacaqGRaGaaeOyaiaabUcacaqGJbGaaeykaaqaai<br />% aaikdaaaaaaaa!3140!<br />\[<br />\begin{gathered}<br /> \left. {\underline {\, <br /> {P.D.Q} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> \frac{1}<br />{{ha}} + \frac{1}<br />{{hb}} + \frac{1}<br />{{hc}} = \frac{1}<br />{\rho } \hfill \\<br /> \hfill \\<br /> {\text{tenemos que saber que la altura se puede encontrar en funcion de los lados}} \hfill \\<br /> \hfill \\<br /> sea:H = \sqrt {s(s - a)(s - b)(s - c)} \hfill \\<br /> \hfill \\<br /> \frac{1}<br />{{\frac{{2H}}<br />{a}}} + \frac{1}<br />{{\frac{{2H}}<br />{b}}} + \frac{1}<br />{{\frac{{2H}}<br />{c}}} = \frac{a}<br />{{2H}} + \frac{b}<br />{{2H}} + \frac{c}<br />{{2H}} = \frac{1}<br />{{2H}}(a + b + c) \hfill \\<br /> \hfill \\<br /> {\text{pero como H es el area de el del triangulo}}{\text{, la cual tambien puede ser expresada}} \hfill \\<br /> {\text{con la siguiente formula}} \hfill \\<br /> \hfill \\<br /> area\vartriangle = \sqrt {s(s - a)(s - b)(s - c)} = \frac{{\rho {\text{(a + b + c)}}}}<br />{2} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaWGKb<br />% Gaam4Baiaad6gacaWGKbGaamyzaiaacQdaaeaaaeaacaWGZbGaeyyp<br />% a0ZaaSaaaeaacaqGOaGaaeyyaiaabUcacaqGIbGaae4kaiaabogaca<br />% qGPaaabaGaaGOmaaaaaeaaaeaacaWGYbGaamyzaiaadwgacaWGTbGa<br />% amiCaiaadYgacaWGHbGaamOEaiaadggacaWGTbGaam4Baiaadohaca<br />% GG6aaabaaabaWaaSaaaeaacaaIXaaabaGaaGOmaiabgwSixpaalaaa<br />% baGaeqyWdiNaaeikaiaabggacaqGRaGaaeOyaiaabUcacaqGJbGaae<br />% ykaaqaaiaaikdaaaaaaiabgwSixlaacIcacaWGHbGaey4kaSIaamOy<br />% aiabgUcaRiaadogacaGGPaGaeyypa0ZaaSaaaeaacaaIXaaabaGaeq<br />% yWdiNaaiikaiaadggacqGHRaWkcaWGIbGaey4kaSIaam4yaiaacMca<br />% aaGaeyyXICTaaiikaiaadggacqGHRaWkcaWGIbGaey4kaSIaam4yai<br />% aacMcacqGHuhY2daqjuaqaamaalaaabaGaaGymaaqaaiabeg8aYbaa<br />% aaaabaaabaGaamyzaiaad6gacaWG0bGaam4Baiaad6gacaWGJbGaam<br />% yzaiaadohaaeaaaeaadaqjEaqaamaalaaabaGaaGymaaqaaiaadIga<br />% caWGHbaaaiabgUcaRmaalaaabaGaaGymaaqaaiaadIgacaWGIbaaai<br />% abgUcaRmaalaaabaGaaGymaaqaaiaadIgacaWGJbaaaiabg2da9maa<br />% laaabaGaaGymaaqaaiabeg8aYbaaaaGaaeiiaiaabgfacaqGUaGaae<br />% yraiaab6cacaqGebaaaaa!937A!<br />\[<br />\begin{gathered}<br /> donde: \hfill \\<br /> \hfill \\<br /> s = \frac{{{\text{(a + b + c)}}}}<br />{2} \hfill \\<br /> \hfill \\<br /> reemplazamos: \hfill \\<br /> \hfill \\<br /> \frac{1}<br />{{2 \cdot \frac{{\rho {\text{(a + b + c)}}}}<br />{2}}} \cdot (a + b + c) = \frac{1}<br />{{\rho (a + b + c)}} \cdot (a + b + c) \Leftrightarrow \left. {\underline {\, <br /> {\frac{1}<br />{\rho }} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> entonces \hfill \\<br /> \hfill \\<br /> \boxed{\frac{1}<br />{{ha}} + \frac{1}<br />{{hb}} + \frac{1}<br />{{hc}} = \frac{1}<br />{\rho }}{\text{ Q}}{\text{.E}}{\text{.D}} \hfill \\ <br />\end{gathered} <br />\]<br />$ si es necesario demostrar alguna igualdad o explicar algun paso, solo posteenlo saludos editado: siempre que escribo mucho en mathytipe me sale tex error Mensaje modificado por naxoobkn el Jan 31 2008, 08:07 PM -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

fs_tol Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 09:35 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad: Universidad: Sexo:	CITA(naxoobkn @ Jan 31 2008, 06:12 PM) $TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGJb<br />% Gaae4Baiaab6gacaqGVbGaae4yaiaabMgacaqGLbGaaeOBaiaabsga<br />% caqGVbGaaeiiaiaabYgacaqGHbGaaeiiaiaabAgacaqGVbGaaeOCai<br />% aab2gacaqG1bGaaeiBaiaabggacaqG6aaabaaabaGaae4CaiaabMga<br />% caqGUbGaaeyqaiaab2cacaqGZbGaaeyAaiaab6gacaqGcbGaaeypai<br />% aabkdacaqGZbGaaeyAaiaab6gadaqadaqaamaalaaabaGaaeyqaiaa<br />% b2cacaqGcbaabaGaaeOmaaaaaiaawIcacaGLPaaacqGHflY1ciGGJb<br />% Gaai4BaiaacohadaqadaqaamaalaaabaGaamyqaiabgUcaRiaadkea<br />% aeaacaaIYaaaaaGaayjkaiaawMcaaaqaaaqaaiaabchacaqGHbGaae<br />% OCaiaabggacaqGGaGaaeOzaiaabggacaqGJbGaaeyAaiaabYgacaqG<br />% PbGaaeizaiaabggacaqGKbGaaeiiaiaabsgacaqGLbGaaeiiaiaabw<br />% gacaqGZbGaae4yaiaabkhacaqGPbGaaeiDaiaabwhacaqGYbGaaeyy<br />% aiaabccacaqGLbGaaeOBaiaabccacaqGTbGaaeyyaiaabshacaqGOb<br />% GaaeiDaiaabMhacaqGWbGaaeyzaiaabccacaqG4bGaaeypaiabeI7a<br />% XbqaaaqaaiGacohacaGGPbGaaiOBaiaaiwdacaWG4bGaeyOeI0Iaci<br />% 4CaiaacMgacaGGUbGaaG4maiaadIhacqGH9aqpdaGcaaqaaiaaikda<br />% aSqabaGcciGGJbGaai4BaiaacohacaaI0aGaamiEaaqaaaqaaiaaik<br />% daciGGZbGaaiyAaiaac6gadaqadaqaamaalaaabaGaaGynaiaadIha<br />% cqGHsislcaaIZaGaamiEaaqaaiaaikdaaaaacaGLOaGaayzkaaGaey<br />% yXICTaci4yaiaac+gacaGGZbWaaeWaaeaadaWcaaqaaiaaiwdacaWG<br />% 4bGaey4kaSIaaG4maiaadIhaaeaacaaIYaaaaaGaayjkaiaawMcaai<br />% abg2da9maakaaabaGaaGOmaaWcbeaakiGacogacaGGVbGaai4Caiaa<br />% isdacaWG4baabaaabaGaaGOmaiGacohacaGGPbGaaiOBaiaadIhacq<br />% GHflY1ciGGJbGaai4BaiaacohacaaI0aGaamiEaiabg2da9maakaaa<br />% baGaaGOmaaWcbeaakiGacogacaGGVbGaai4CaiaaisdacaWG4baaba<br />% aabaGaci4CaiaacMgacaGGUbGaamiEaiabg2da9maalaaabaWaaOaa<br />% aeaacaaIYaaaleqaaaGcbaGaaGOmaaaaaeaaaeaadaqjEaqaaiaadI<br />% hacqGH9aqpcaaI0aGaaGynaaaaaaaa!D428!<br />\[<br />\begin{gathered}<br /> {\text{conociendo la formula:}} \hfill \\<br /> \hfill \\<br /> {\text{sinA - sinB = 2sin}}\left( {\frac{{{\text{A - B}}}}<br />{{\text{2}}}} \right) \cdot \cos \left( {\frac{{A + B}}<br />{2}} \right) \hfill \\<br /> \hfill \\<br /> {\text{para facilidad de escritura en mathtype x = }}\theta \hfill \\<br /> \hfill \\<br /> \sin 5x - \sin 3x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin \left( {\frac{{5x - 3x}}<br />{2}} \right) \cdot \cos \left( {\frac{{5x + 3x}}<br />{2}} \right) = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> 2\sin x \cdot \cos 4x = \sqrt 2 \cos 4x \hfill \\<br /> \hfill \\<br /> \sin x = \frac{{\sqrt 2 }}<br />{2} \hfill \\<br /> \hfill \\<br /> \boxed{x = 45} \hfill \\ <br />\end{gathered} <br />\]<br />$ saludos editado: con respeto a la 1 se podria decir que p (rho) es circunradio? ¿Qué pasa si 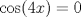$TEX: $\cos(4x)=0$$ ? 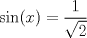Además 45º no es la única solución de $TEX: $\sin(x)=\dfrac{1}{\sqrt{2}}$$ Saludos -------------------- $TEX: $CARITA$$

Ictio Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 31 2008, 10:08 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 309 Registrado: 28-July 07 Desde: Copiapó-Santiago Miembro Nº: 7.899 Nacionalidad: Universidad: Sexo:	CITA(Abu-Khalil @ Jan 4 2008, 01:01 AM) No sé si ta bn, pq no sé trabajar mucho con ecuaciones trigonométricas pero al menos el resultado tiene sentido D: ! $TEX: \begin{equation}\begin{aligned}<br />\arccos{x} - \arcsin{x} &= \arccos{x\sqrt{3}}\\<br />\theta_1 - (\dfrac{\pi}{2} - \theta_1) &= \theta_2\\<br />2\theta_1 - \dfrac{\pi}{2} &= \theta_2\\<br />\sin{(2\theta_1-\dfrac{\pi}{2})} &= \sin{\theta_2}\\<br />\sin{2\theta_1}\cos{\dfrac{\pi}{2}}-\sin{\dfrac{\pi}{2}}\cos{2\theta_1} &= \sin{\theta_2}\\<br />-\cos^2{\theta_1}+\sin^2{\theta_1} &= \sin{\theta_2}\\<br />(1-x^2) - x^2 &= \sqrt{1-3x^2}\\<br />4x^4 - 4x^2 &= 3x^2\\<br />x^2(4x^2-1) &= 0\\<br />x &= \dfrac{1}{2}\\<br />\end{aligned}\end{equation}$ Solución alternativa Primero, recordaremos un par de hechos conocidos: $TEX: Recuerdo: \\<br />\begin{equation}<br />\begin{aligned}<br />\cos \theta &= \sqrt{1-\operatorname{sen}^2 \theta }\\<br />\cos (\operatorname{arcsen} x) &= \sqrt{1-x^2}\\<br />\\<br />\operatorname{sen} \theta &= \sqrt{1-\cos^2 \theta }\\<br />\operatorname{sen} (\arccos x) &= \sqrt{1-x^2}<br />\end{aligned}<br />\end{equation}<br />Tenemos por resolver <br />\begin{equation}<br />\begin{aligned}<br />\arccos{x} - \arcsin{x} &= \arccos{x\sqrt{3}} \qquad \big/ \cos ( )\\<br />\cos (\arccos x - \operatorname{arcsen} x) &= x\sqrt 3\\<br />x\cdot \cos (\operatorname{arcsen} x) + x\cdot \operatorname{sen} (\arccos x) &= x\sqrt 3\\<br />\not x \cdot (\cos (\operatorname{arcsen} x) + \operatorname{sen} (\arccos x)) &= \not x \sqrt 3\\<br />\sqrt{1-x^2} + \sqrt{1-x^2} &= \sqrt 3\\<br />2\sqrt{1-x^2} &= \sqrt 3 \qquad \big/ ( )^2 \\<br />4(1-x^2) &= 3\\<br />4-4x^2 &= 3\\<br />4x^2 &= 1\\<br />x^2 &= \dfrac14 \\<br />x &= \pm \dfrac12<br />\end{aligned}<br />\end{equation}<br /><br />Si no me equivoco, $\arccos$ no admite valores negativos en su dominio por lo que $x$ sería $\dfrac12$$ --------------------

« Posterior · Geometría · Anterior »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 10th April 2025 - 11:49 AM