|
|
|
|
|
|
|
  |
 Jan 28 2006, 04:13 PM Jan 28 2006, 04:13 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
En esta unidad se introducira este tema interesante de Teoria de numeros, que es fundamental para entender otros contenidos que se profundizaran mas adelante en este sector. Comenzaremos con dos definiciones.
Definicion 1: Sean 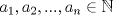 . El maximo comun divisor de . El maximo comun divisor de 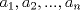 es el mayor numero es el mayor numero 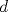 tal que tal que 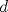 divide a divide a 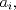 para para 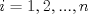 . Esto quiere decir, . Esto quiere decir, 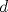 divide a divide a 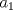 , , 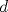 divide a divide a 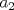 ,..., ,...,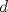 divide a divide a 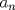 . Usualmente escribimos esto como . Usualmente escribimos esto como 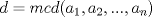 , , 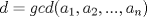 (proveniente de greatest common divisor) o (proveniente de greatest common divisor) o 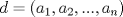 . En este topic se ocupara por comodidad la primera notacion presentada. . En este topic se ocupara por comodidad la primera notacion presentada. Ejemplo 1: Calcule el maximo comun divisor entre  Solucion: Veamos que  , , 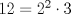 , , 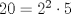 . Los factores primos en estos 3 numeros a la vista son . Los factores primos en estos 3 numeros a la vista son 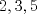 , entonces , entonces 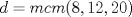 posee a posee a 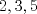 como factores primos. Pero como factores primos. Pero  no divide a no divide a 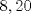 y y 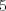 no divide a no divide a 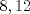 . Sin embargo, . Sin embargo, 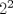 si divide a si divide a 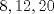 por lo que por lo que 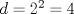  Definicion 2: Sean 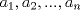 naturales. El minimo comun multiplo de naturales. El minimo comun multiplo de 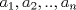 es el menor natural es el menor natural 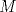 tal que tal que 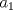 divide a divide a 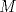 , , 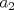 divide a divide a 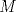 ,.., ,..,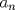 divide a divide a 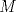 . Se escribe usualmente como . Se escribe usualmente como 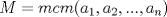 , , 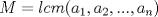 (proveniente del ingles leatest common multiple) o (proveniente del ingles leatest common multiple) o ![TEX: $M=[a_1, a_2,...,a_n]$](./tex/639cb1649a70e752df49955dcd442b62.png) Por comodidad, se ocupara la primera notacion. Por comodidad, se ocupara la primera notacion. Ejemplo 2: Calcule el minimo comun multiplo entre 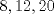 Solucion: Veamos que  , , 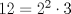 ,y ,y 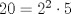 . Al igual que en el ejemplo 1, debemos notar que los factores primos que podemos ver a simple vista son . Al igual que en el ejemplo 1, debemos notar que los factores primos que podemos ver a simple vista son 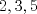 . Claramente . Claramente 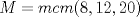 es multiplo de es multiplo de 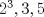 y luego y luego 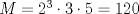  Ahora... con estas dos definiciones estamos en condicion de intentar los dos siguientes problemas -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Oct 11 2009, 08:49 PM Oct 11 2009, 08:49 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problemas:
Problema 1: Considere la recta 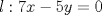 en el plano cartesiano, con origen en el plano cartesiano, con origen 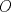 . Sea . Sea 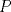 un punto de un punto de  cuya abscisa es cuya abscisa es 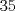 . ¿Cuantos puntos . ¿Cuantos puntos 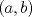 de coordenadas enteras tiene el segmento de coordenadas enteras tiene el segmento 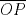 ? ? A) 2 puntos B) 6 puntos C) 7 puntos D) 8 puntos E) Ninguna de las anteriores (Un presente para el team PSU) Problema 2: Sebastian, Matias y Ricardo son muy metodicos para sus compras. Sebastian va cada 12 dias al almacen de David, Matias cada 15 dias y Ricardo cada 10 dias. Si hoy Viernes, se reunieron los 3 en el almacen, que dia de la semana se reuniran la proxima vez? A) Miercoles B) Jueves C) Viernes D) Sabado E) Ninguna de los anteriores. (Otro presente para el team PSU) Solucion: Problema 3: Sean 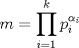 y y 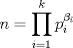 las factorizaciones aritmeticas de las factorizaciones aritmeticas de 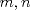 respectivamente. Sean respectivamente. Sean 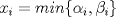 y y 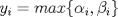 para para 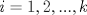 . Demuestre que: . Demuestre que:i) 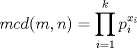 ii) 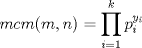 iii) 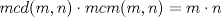 Problema 4: Demuestre que si 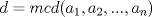 , entonces: , entonces: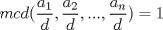 Problema 5: Sea 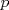 un numero primo. Determine todos los posibles valores de un numero primo. Determine todos los posibles valores de 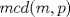 , con , con  natural. natural. Problema 6: Sea 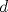 un divisor comun de un divisor comun de 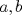 (esto es, (esto es, 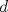 divide a divide a  y y 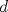 divide a divide a  ). Demuestre que ). Demuestre que 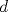 divide a divide a 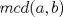 . ¿Es posible generalizar esto? . ¿Es posible generalizar esto?Problema 7: Sea 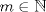 . Demuestre que: . Demuestre que: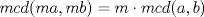 Problema 8: Dado 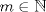 , asuma que podemos hallar , asuma que podemos hallar 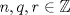 tales que tales que 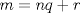 . Demuestre que . Demuestre que 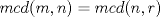 Problema 9: Sea 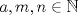 , con , con 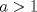 . Sea . Sea 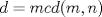 . Demuestre que: . Demuestre que: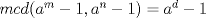 Problema 10: Se tiene un rectángulo de lados enteros 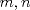 se subdivide en se subdivide en  cuadraditos de lado 1. Encontrar el número de cuadraditos que son atravesados por la diagonal (sin contabilizar los que son tocados sólo en un vértice) cuadraditos de lado 1. Encontrar el número de cuadraditos que son atravesados por la diagonal (sin contabilizar los que son tocados sólo en un vértice)(I Olimpiada nacional de matematicas, 1989) continuara..... atentos que se vienen mas problemas -------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Oct 11 2009, 09:32 PM Oct 11 2009, 09:32 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.103 Registrado: 31-March 06 Desde: Santiago de Chile Miembro Nº: 739 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Solución problema 1.
Notar que: ![TEX: <br />\[\begin{gathered}<br /> P(x,y) = (35,y) \in l,{\text{ luego:}} \hfill \\<br /> 7(35) = 5y \Rightarrow y = 7 \times 7 \times 5 = 5y \hfill \\<br /> \therefore y = 49 \Rightarrow P(x,y) = (35,49). \hfill \\ <br />\end{gathered} \]<br />](./tex/68e5460597d7599c1f472faafd989853.png) Además: ![TEX: <br />\[\begin{gathered}<br /> mcm(7,5) = 7 \times 5 = 35 \hfill \\<br /> mcd(7,5) = 1 \hfill \\ <br />\end{gathered} \]<br />](./tex/3cb3ac6f73638e069adf59208bb1bcaf.png) Los pares ![TEX: <br />\[(a,b);a,b \in \mathbb{Z}\]<br />](./tex/2ad2a993fc60abd75a837365fb226d2e.png) son mayores o iguales son mayores o iguales a cero (tomando en cuenta el segmento ![TEX: <br />\[\overline {OP} \]<br />](./tex/f7aa7ef46266a9f121950ea07463877c.png) ), cumplen con la igualdad ), cumplen con la igualdad ![TEX: <br />\[7a = 5b\]<br />](./tex/ef77afd3d6b48d5102ff1d9abae08272.png) y además y además ![TEX: <br />\[b \leqslant 49\]<br />](./tex/72e44dfbfdc0ec191b3d5ab21d53badd.png) ![TEX: % MathType!MTEF!2!1!+-<br />% feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbd9wBPn<br />% gitfMBZbsttbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhi<br />% ov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-<br />% Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq<br />% 0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaq<br />% aafaaakqaabeqaaiabgsJiCjaabccacaqGSbGaae4BaiaabohacaqG<br />% GaGaaeiCaiaabwhacaqGUbGaaeiDaiaab+gacaqGZbGaaeiiaiaabI<br />% cacaqGHbGaaeilaiaabkgacaqGPaGaeyicI48aa0aaaeaacaWGpbGa<br />% amiuaaaacaqGGaGaaeyCaiaabwhacaqGLbGaaeiiaiaabogacaqG1b<br />% GaaeyBaiaabchacaqGSbGaaeyzaiaab6gacaqGGaGaaeiBaiaab+ga<br />% caqGGaaabaGaaeiCaiaabwgacaqGKbGaaeyAaiaabsgacaqGVbGaae<br />% iiaiaabohacaqGVbGaaeOBaiaabccacaqGYaGaaeilaiaabccacaqG<br />% HbGaaeiiaiaabohacaqGHbGaaeOyaiaabwgacaqGYbGaae4oaiaabc<br />% cacaqGOaGaaeimaiaabYcacaqGWaGaaeykaiaabUdacaqGGaGaaeik<br />% aiaabodacaqG1aGaaeilaiaabsdacaqG5aGaaeykaaaaaa!77E8!<br />\[\begin{gathered}<br /> \therefore {\text{ los puntos (a}}{\text{,b)}} \in \overline {OP} {\text{ que cumplen lo }} \hfill \\<br /> {\text{pedido son 2}}{\text{, a saber; (0}}{\text{,0); (35}}{\text{,49)}} \hfill \\ <br />\end{gathered} \]<br />](./tex/6e0687f8364d60f65687e4684bbdd9e3.png) Mensaje modificado por Shinichi el Oct 11 2009, 09:37 PM -------------------- "Caer, Aprender, Levantarse y Seguir" R.C.B.
"Education is an admirable thing, but it is well to remember from time to time that nothing worth knowing can be taught". Oscar Wilde, “The Critic as Artist,” 1890. "That's the reason they're called lessons, because they lesson from day to day". Lewis Carroll |
|
|
|
 Oct 11 2009, 09:43 PM Oct 11 2009, 09:43 PM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Respuesta incorrecta, Shinichi, que me dices del punto
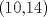 ?? ??-------------------- Ricardo Vargas Obando
Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile.  Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico:
|
|
|
|
 Oct 11 2009, 09:45 PM Oct 11 2009, 09:45 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.169 Registrado: 11-June 08 Desde: rancagua Miembro Nº: 26.922 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Problema 2
Notemos que el MCM es 60 entonces: en 60 dias mas se juntaran de nuevo, como se juntaron un dia viernes, en 56 dias mas vlvera a ser viernes luego falta 4 dias mas para 60 dias, entonces se volveran a juntar un dia martes en conclusion Alternativa E Mensaje modificado por Kain #13 el Oct 11 2009, 10:14 PM -------------------- Richard Fabian Jerez
Ex alumno del Liceo Oscar Castro 4ºL matemático ¿Necesitas ayuda para la psu y no tienes dinero?: Agrega a logratus850@hotmail.com y comienza a preguntar! Somos un grupo de universitarios dispuestos a ayudarte de manera gratuita para que logres tus sueños, todos tuvimos como promedio más de 800 puntos en la PSU. Team PSU 2010!! Únete!  [color="#000080"][/color] [color="#000080"][/color] |
|
|
|
 Oct 11 2009, 09:58 PM Oct 11 2009, 09:58 PM
Publicado:
#6
|
|
 Dios Matemático Supremo Grupo: Team Ensayos FMAT Mensajes: 1.103 Registrado: 31-March 06 Desde: Santiago de Chile Miembro Nº: 739 Nacionalidad:  Colegio/Liceo:  Sexo:  |
Noté algo "interesante" entre los a,b de los puntos (a,b), pero no se cómo formalizarlo.
![TEX: % MathType!MTEF!2!1!+-<br />% feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2Caerbd9wBPn<br />% gitfMBZbsttbqedmvETj2BSbqefm0B1jxALjhiov2DaerbuLwBLnhi<br />% ov2DGi1BTfMBaebbnrfifHhDYfgasaacH8srps0lbbf9q8WrFfeuY-<br />% Hhbbf9v8qqaqFr0xc9pk0xbba9q8WqFfea0-yr0RYxir-Jbba9q8aq<br />% 0-yq-He9q8qqQ8frFve9Fve9Ff0dmeaabaqaciGacaGaaeqabaWaaq<br />% aafaaakqaabeqaaiaabYeacaqGVbGaae4CaiaabccacaqGWbGaaeyD<br />% aiaab6gacaqG0bGaae4BaiaabohacaqGGaGaaeikaiaabggacaqGSa<br />% GaaeOyaiaabMcacaqGGaGaaeiCaiaab+gacaqGKbGaaeyzaiaab2ga<br />% caqGVbGaae4CaiaabccacaqG2bGaaeyzaiaabkhacaqGSbGaae4Bai<br />% aabohacaqGGaGaae4yaiaab+gacaqGTbGaae4BaaqaaiaabcfacaqG<br />% OaGaaeyyaiaabYcacaqGIbGaaeykaiaab2dacaqGOaGaaeynaiaabI<br />% hacaqGSaGaae4naiaabMhacaqGPaGaaeilaiaabccacaqGJbGaae4B<br />% aiaab6gacaqGGaGaaeiEaiaabYcacaqG5bGaaeiiaiaabwgacaqGUb<br />% GaaeiDaiaabwgacaqGYbGaae4BaiaabohacaqGUaaabaGaaeyqaiaa<br />% bsgacaqGLbGaaeyBaiaabgoacaqGZbGaaeiiaiaabwgacaqGUbGaae<br />% iDaiaabkhacaqGLbGaaeiiaiaabsgacaqGVbGaae4CaiaabccacaqG<br />% WbGaaeyDaiaab6gacaqG0bGaae4BaiaabohacaqGGaGaae4yaiaab+<br />% gacaqGUbGaae4CaiaabwgacaqGJbGaaeyDaiaabshacaqGPbGaaeOD<br />% aiaab+gacaqGZbGaaeiiaaqaaiaabIcacaqG4bGaaeilaiaabMhaca<br />% qGPaGaaeiiaiaabwgacaqGSbGaaeyzaiaabEgacaqGPbGaaeizaiaa<br />% b+gacaqGZbGaaeiiaiaabwgacaqG4bGaaeyAaiaabohacaqG0bGaae<br />% yzaiaabccacaqG1bGaaeOBaiaabggacaqGGaGaaeizaiaabMgacaqG<br />% MbGaaeyzaiaabkhacaqGLbGaaeOBaiaabogacaqGPbGaaeyyaiaabc<br />% cacaqGKbGaaeyzaiaabccacaqG1aGaaeiiaiaabwhacaqGUbGaaeyA<br />% aiaabsgacaqGHbGaaeizaiaabwgacaqGZbGaaeilaaqaaiaabwgaca<br />% qGZbGaaeiDaiaab+gacaqGGaGaaeyzaiaabohacaqG6aGaaeiiaaqa<br />% aiaabofacaqGPbGaaeiiaiaabcfacaqGOaGaaeyyaiaabYcacaqGIb<br />% Gaaeykaiaab2dacaqGOaGaaeynaiaabIhacaqGSaGaae4naiaabMha<br />% caqGPaGaaeiiaiabgIGiopaanaaabaGaam4taiaadcfaaaGaeyO0H4<br />% TaamiuaiaacEcacaGGOaGaamyyaiaacYcacaWGIbGaaiykaiabg2da<br />% 9iaacIcacaaI1aGaai4waiaadIhacqGHRaWkcaaI1aGaaiyxaiaacY<br />% cacaaI3aGaai4waiaadMhacqGHRaWkcaaI1aGaaiyxaiaacMcacqGH<br />% iiIZdaqdaaqaaiaad+eacaWGqbaaaaaaaa!F28A!<br />\[\begin{gathered}<br /> {\text{Los puntos (a}}{\text{,b) podemos verlos como}} \hfill \\<br /> {\text{P(a}}{\text{,b) = (5x}}{\text{,7y)}}{\text{, con x}}{\text{,y enteros}}{\text{.}} \hfill \\<br /> {\text{Adem\'a s entre dos puntos consecutivos }} \hfill \\<br /> {\text{(x}}{\text{,y) elegidos existe una diferencia de 5 unidades}}{\text{,}} \hfill \\<br /> {\text{esto es: }} \hfill \\<br /> {\text{Si P(a}}{\text{,b) = (5x}}{\text{,7y) }} \in \overline {OP} \Rightarrow P'(a,b) = (5[x + 5],7[y + 5]) \in \overline {OP} \hfill \\ <br />\end{gathered} \]<br />](./tex/79889167fd1ceca029aa4f6ea8619ed0.png) Se que es sólo una conjetura, pero si de alguna forma pudiera formalizar esta intuición, el problema saldría más fácil. Saludos PD: Aún me falta mucho -------------------- "Caer, Aprender, Levantarse y Seguir" R.C.B.
"Education is an admirable thing, but it is well to remember from time to time that nothing worth knowing can be taught". Oscar Wilde, “The Critic as Artist,” 1890. "That's the reason they're called lessons, because they lesson from day to day". Lewis Carroll |
|
|
|
 Oct 11 2009, 10:21 PM Oct 11 2009, 10:21 PM
Publicado:
#7
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.244 Registrado: 11-October 09 Desde: Santiago Miembro Nº: 60.148 Nacionalidad:  Universidad:  Sexo:  |
Problema 2
Primero debemos encontrar el minimo comum multiplo (m.c.m) entre 12, 15, 10 Tomamos las bases primas 2^2*3=12 3*5=15 2*5=10 De estas tenemos a 2^2, 3, 5. Multiplicamos cada termino y nos daria 60. Esto lo dividimos por 7 (por los dia ke trae la semana) y de esta division nos dara un resto que seria igual a 4. 60/7 = 8 resto= 4 Pasaran 8 semanas para volverse a encontrar, y 4 dias a contar del dia viernes, por lo tanto se encontraran un dia martes si no me equivoco -------------------- |
|
|
|
 Oct 14 2009, 07:02 AM Oct 14 2009, 07:02 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 2.139 Registrado: 11-June 08 Desde: UK Miembro Nº: 26.837 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
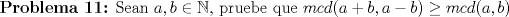 ![TEX: \begin{flushleft}\textbf{Problema 12:} Sean $a,b\in{\Bbb N}$ tal que $mcd(a,b)\not= 1$, entonces pruebe que $mcd(a,b)|mcm(a,b)$ pero $[mcd(a,b)]^2\nmid mcm(a,b)$<br /><br />\end{flushleft}<br />](./tex/f288fddf8aabca9a5157345086e9796d.png)  saludos -------------------- blep
|
|
|
|
 May 4 2011, 09:26 AM May 4 2011, 09:26 AM
Publicado:
#9
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 4.874 Registrado: 19-January 07 Desde: Mathematics!! Miembro Nº: 3.830 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
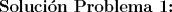 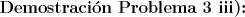 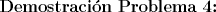 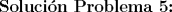 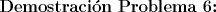 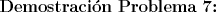 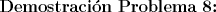 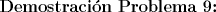 Saludos y espero que estén bien mis resultados, todavía quedan algunos por resolver. --------------------  "... Lo veo, pero no puedo creerlo ... se trata de mostrar que las superficies, los volúmenes e incluso las variedades continuas de n dimensiones pueden ponerse en correspondencia unívoca con curvas continuas, o sea, con variedades de una sola dimensión, y que por consiguiente, las superficies, los volúmenes y las variedades de n dimensiones tienen también la misma potencia que las curvas ..." G. Cantor. Las Matemáticas son el lenguaje de la naturaleza, todo lo que nos rodea se puede representar y entender mediante números. Si se hace un gráfico con los números de un sistema, se forman modelos; éstos modelos están por todas partes en la naturaleza. Max Cohen.  Licenciado en Matemática (2021). Universidad de Concepción, Chile. |
|
|
|
 Sep 1 2011, 03:48 PM Sep 1 2011, 03:48 PM
Publicado:
#10
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 43 Registrado: 5-August 10 Miembro Nº: 75.027 Sexo:  |
Problema 13
Mensaje modificado por dieguindiegao el Sep 1 2011, 04:49 PM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 18th February 2025 - 06:10 PM |











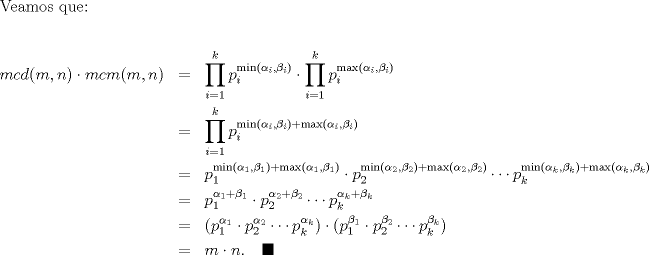



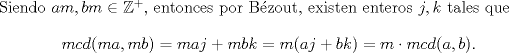
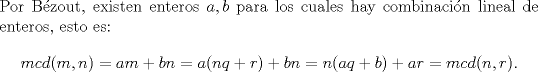

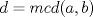 entonces existen enteros
entonces existen enteros 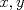 tales que
tales que 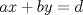 . En efecto consideremos al conjunto
. En efecto consideremos al conjunto 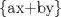 con
con 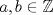 . Luego, sea
. Luego, sea 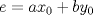 el menor elemento del conjunto en cuestión. Luego, no es difícil notar que
el menor elemento del conjunto en cuestión. Luego, no es difícil notar que 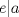 y
y 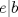 , pues si
, pues si  no dividiera a
no dividiera a  entonces deben existir enteros
entonces deben existir enteros 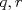 tales que
tales que 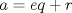 con
con 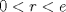 . Pero,
. Pero, 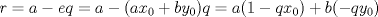 , es decir
, es decir  pertenece al conjunto
pertenece al conjunto 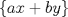 , lo que contradice nuestra minimilidad supuesta. Entonces
, lo que contradice nuestra minimilidad supuesta. Entonces 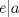 . De forma análoga se prueba que
. De forma análoga se prueba que 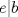 . Ahora solo nos resta probar que
. Ahora solo nos resta probar que 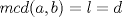 . En efecto, dado que
. En efecto, dado que 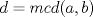 existen enteros
existen enteros 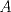 y
y 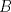 tales que
tales que 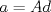 y
y  . Luego,
. Luego, 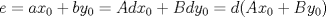 . De ésto último se desprende que
. De ésto último se desprende que 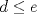 . Ahora, claramente no puede ocurrir que
. Ahora, claramente no puede ocurrir que 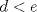 . Luego
. Luego 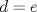 .
. 