C1 Lic. en Matemática - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Geometría

2 Páginas:

1 2 >

Reply to this topic

Start new topic

C1 Lic. en Matemática, MAT1305

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2007, 01:10 PM Publicado: #1
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \begin{enumerate}\item Desde un monumento de 80 m de alto, los \'angulos de depresi\'on de dos objetos situados en el suelo al oeste del monumento son de $45^\circ$ y $30^\circ.$ Determine la distancia entre los objetos.\item\begin{enumerate}\item[a) ] Demuestre que: $ \cos ^2 \beta \cdot \cot \beta + \operatorname{sen} ^2 \beta \cdot \operatorname{tg} \beta + \operatorname{sen} 2\beta = \operatorname{tg} \beta + \cot \beta .$\item[b) ] Demuestre que: $ \operatorname{sen} ^2 \beta + \operatorname{sen} ^2 \left( {\frac{2}<br />{3}\pi + \beta } \right) + \operatorname{sen} ^2 \left( {\frac{2}<br />{3}\pi - \beta } \right) = \frac{3}<br />{2}.$\end{enumerate}\item Demuestre que: $ \dfrac{{\operatorname{sen} \beta + \operatorname{sen} 2\beta + \operatorname{sen} 4\beta + \operatorname{sen} 5\beta }}<br />{{\cos \beta + \cos 2\beta + \cos 4\beta + \cos 5\beta }} = \operatorname{tg} 3\beta .$\end{enumerate}$ Mensaje modificado por Pily el Dec 28 2007, 06:15 PM --------------------

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 24 2007, 06:19 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Calentando motores pa la U 1. Tenemos la sgte. situación: $TEX: \begin{equation}\begin{aligned}<br />\tan{60º} &= \dfrac{\overline{AC}}{80[m]} &= \sqrt{3} \\<br />\Longrightarrow \overline{AC} &= 80\sqrt{3} [m]<br />\end{aligned}\end{equation}$ Y, $TEX: \begin{equation}\begin{aligned}<br />\tan{45º} &= \dfrac{\overline{DC}}{80[m]} &= 1 \\<br />\Longrightarrow \overline{DC} &= 80[m]<br />\end{aligned}\end{equation}$ $TEX: \begin{equation}\begin{aligned}<br />\Longrightarrow \overline{AD} &= 80 (\sqrt{3} - 1 )[m]<br />\end{aligned}\end{equation}$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

PXO11 Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2007, 02:58 AM Publicado: #3
Matemático Grupo: Usuario FMAT Mensajes: 64 Registrado: 6-April 07 Miembro Nº: 4.985 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \textbf{2b)} Demuestre que: $sen^2\beta+sen^2(\dfrac{2\pi}{3}+\beta)+sen^2(\dfrac{2\pi}{3}-\beta)=\dfrac{3}{2}$.\\\\Por suma y diferencia de senos se tiene que:\\\\$sen^2\beta+sen^2(\dfrac{2\pi}{3}+\beta)+sen^2(\dfrac{2\pi}{3}-\beta)=sen^2\beta+\left(sen(\dfrac{2\pi}{3})cos\beta+cos(\dfrac{2\pi}{3})sen\beta\right)^2+\left(sen(\dfrac{2\pi}{3})cos\beta-cos(\dfrac{2\pi}{3})sen\beta\right)^2$\\Como sabemos que $sen(\dfrac{2\pi}{3})=\dfrac{\sqrt{3}}{2}$ y $cos(\dfrac{2\pi}{3})=\dfrac{-1}{2}$ tenemos que lo anterior es equivalente a:\\\\$sen^2\beta+\left(\dfrac{\sqrt{3}cos\beta}{2}-\dfrac{sen\beta}{2}\right)^2+\left(\dfrac{\sqrt{3}cos\beta}{2}+\dfrac{sen\beta}{2}\right)^2$ elevando al cuadrado los par\'entesis(cuadrados de binomio) y sum\'andolos se tiene que lo anterior es equivalente a:\\\\$$sen^2\beta+\dfrac{6cos^2\beta+2sen^2\beta}{4}$$sumando las expresiones y factorizando se tiene$$\dfrac{6(cos^2\beta+sen^2\beta)}{4}$$y como sabemos que $cos^2\beta+sen^2\beta=1$ simplificando se obtiene que lo anterior equivale a $\dfrac{3}{2}$, concluyendo lo pedido $\blacksquare$$ La 2a) me parece que tiene un error xD es fácil comprobarlo con beta=pi/6 y la 3) es muy larga para postearla aunque debe haber un método más directo que el que usé, el método cortito està abajo hecho por fs_tol xD Mensaje modificado por PXO11 el Dec 26 2007, 02:11 PM

fs_tol Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 26 2007, 03:58 AM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 670 Registrado: 30-January 06 Desde: Ñuñoa, Santiago Miembro Nº: 524 Nacionalidad: Universidad: Sexo:	CITA(PXO11 @ Dec 26 2007, 04:58 AM) la 3) es muy larga para postearla aunque debe haber un método más directo que el que usé De hecho la 3 es la más corta xD, si recordamos que 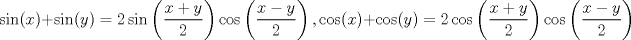$TEX: $\sin(x)+\sin(y)=2\sin\left(\dfrac{x+y}{2}\right)\cos\left(\dfrac{x-y}{2}\right), \cos(x)+\cos(y)=2\cos\left(\dfrac{x+y}{2}\right)\cos\left(\dfrac{x-y}{2}\right)$$ entonces agrupamos los términos con 1 y 5 beta y los con 2 y 4 beta en el numerador y denominador, y reducimos los factores 2, quedando 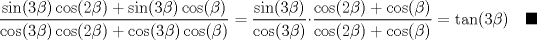$TEX: $\noindent \dfrac{\sin(3\beta)\cos(2\beta)+\sin(3\beta)\cos(\beta)}{\cos(3\beta)\cos(2\beta)+\cos(3\beta)\cos(\beta)} = \dfrac{\sin(3\beta)}{\cos(3\beta)}\cdot\dfrac{\cos(2\beta)+\cos(\beta)}{\cos(2\beta)+\cos(\beta)} = \tan(3\beta) \quad \blacksquare$$ Notar que la identidad no se cumple siempre, ya que la última fracción se indetermina si 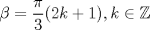$TEX: $\beta=\dfrac{\pi}{3}(2k+1), k \in \mathbb{Z}$$ , mientras que $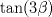TEX: $\tan(3\beta)$$ existe para todos estos valores. Saludos -------------------- $TEX: $CARITA$$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 28 2007, 12:18 AM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(PXO11 @ Dec 26 2007, 05:58 AM) La 2a) me parece que tiene un error xD es fácil comprobarlo con beta=pi/6 y la 3) es muy larga para postearla aunque debe haber un método más directo que el que usé, el método cortito està abajo hecho por fs_tol xD Yo probé tb con $TEX: $\dfrac{\pi}{6}$$ y tpco me dió, en volá falta un cuadrao por ahí o:? Asumo que la forma larga es esta xD: 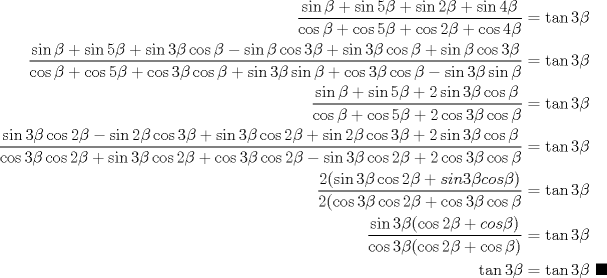$TEX: \begin{equation}\begin{aligned}<br />\dfrac{\sin{\beta}+\sin{5\beta}+\sin{2\beta}+\sin{4\beta}}{\cos{\beta}+\cos{5\beta}+ \cos{2\beta}+\cos{4\beta}} &= \tan{3\beta}\\<br />\dfrac{\sin{\beta} + \sin{5\beta} + \sin{3\beta}\cos{\beta} - \sin{\beta}\cos{3\beta} + \sin{3\beta}\cos{\beta} + \sin{\beta}\cos{3\beta}}{\cos{\beta} + \cos{5\beta} + \cos{3\beta}\cos{\beta} + \sin{3\beta}\sin{\beta} + \cos{3\beta}\cos{\beta} - \sin{3\beta}\sin{\beta}} &= \tan{3\beta}\\<br />\dfrac{\sin{\beta} + \sin{5\beta} + 2\sin{3\beta}\cos{\beta}}{\cos{\beta} + \cos{5\beta} + 2\cos{3\beta}\cos{\beta}} &= \tan{3\beta}\\<br />\dfrac{\sin{3\beta}\cos{2\beta}-\sin{2\beta}\cos{3\beta}+\sin{3\beta}\cos{2\beta}+\sin{2\beta}\cos{3\beta}+ 2\sin{3\beta}\cos{\beta}}{\cos{3\beta}\cos{2\beta}+\sin{3\beta}\cos{2\beta}+\cos{3\beta}\cos{2\beta}- \sin{3\beta}\cos{2\beta} +2\cos{3\beta}\cos{\beta}} &= \tan{3\beta}\\<br />\dfrac{2(\sin{3\beta}\cos{2\beta}+sin{3\beta}cos{\beta})}{2(\cos{3\beta}\cos{2\beta}+\cos{3\beta}\cos{\beta}} &= \tan{3\beta}\\<br />\dfrac {\sin{3\beta}(\cos{2\beta}+cos{\beta})}{\cos{3\beta}(\cos{2\beta}+\cos{\beta})} &= \tan{3\beta}\\<br />\tan{3\beta}&= \tan{3\beta}\ \blacksquare\\ <br />\end{aligned}\end{equation}$ Bleh, se veía más corta en el papel xD. Mensaje modificado por Abu-Khalil el Dec 28 2007, 01:06 AM -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 28 2007, 06:18 PM Publicado: #6
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	Disculpen, había un cuadrado demás. Mensaje anterior editado . --------------------

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 28 2007, 09:00 PM Publicado: #7
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	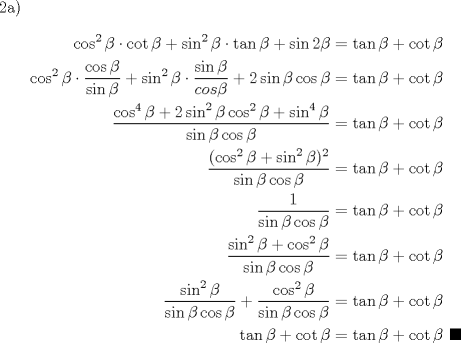$TEX: 2a) \begin{equation}\begin{aligned}<br />\cos^2{\beta} \cdot \cot{\beta} + \sin^2{\beta} \cdot \tan{\beta} + \sin{2\beta} &= \tan{\beta}+\cot{\beta}\\<br />\cos^2{\beta} \cdot \dfrac{\cos{\beta}}{\sin{\beta}} + \sin^2{\beta} \cdot \dfrac{\sin{\beta}}{cos{\beta}} + 2\sin{\beta}\cos{\beta} &= \tan{\beta}+\cot{\beta}\\<br />\dfrac{\cos^4{\beta}+2\sin^2{\beta}\cos^2{\beta}+\sin^4{\beta}}{\sin{\beta}\cos{\beta}} &= \tan{\beta}+\cot{\beta}\\<br />\dfrac{(\cos^2{\beta}+\sin^2{\beta})^2}{\sin{\beta}\cos{\beta}} &= \tan{\beta}+\cot{\beta}\\<br />\dfrac{1}{\sin{\beta}\cos{\beta}}&= \tan{\beta}+\cot{\beta}\\<br />\dfrac{\sin^2{\beta}+\cos^2{\beta}}{\sin{\beta}\cos{\beta}}&= \tan{\beta}+\cot{\beta}\\<br />\dfrac{\sin^2{\beta}}{\sin{\beta}\cos{\beta}} + \dfrac{\cos^2{\beta}}{\sin{\beta}\cos{\beta}} &= \tan{\beta}+\cot{\beta}\\<br />\tan{\beta}+\cot{\beta} &= \tan{\beta}+\cot{\beta} \ \blacksquare\\<br />\end{aligned}\end{equation}$ PD: Editado. Mensaje modificado por Abu-Khalil el Dec 30 2007, 05:46 PM -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

XaPi Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 28 2007, 09:46 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.872 Registrado: 9-March 06 Desde: Welcome Miembro Nº: 614 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	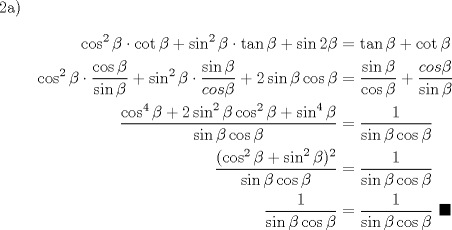CITA(Abu-Khalil @ Dec 29 2007, 12:00 AM) $TEX: 2a) \begin{equation}\begin{aligned}<br />\cos^2{\beta} \cdot \cot{\beta} + \sin^2{\beta} \cdot \tan{\beta} + \sin{2\beta} &= \tan{\beta}+\cot{\beta}\\<br />\cos^2{\beta} \cdot \dfrac{\cos{\beta}}{\sin{\beta}} + \sin^2{\beta} \cdot \dfrac{\sin{\beta}}{cos{\beta}} + 2\sin{\beta}\cos{\beta} &= \dfrac{\sin{\beta}}{\cos{\beta}} + \dfrac{cos{\beta}}{\sin{\beta}}\\<br />\dfrac{\cos^4{\beta}+2\sin^2{\beta}\cos^2{\beta}+\sin^4{\beta}}{\sin{\beta}\cos{\beta}} &= \dfrac{1}{\sin{\beta}\cos{\beta}}\\<br />\dfrac{(\cos^2{\beta}+\sin^2{\beta})^2}{\sin{\beta}\cos{\beta}} &= \dfrac{1}{\sin{\beta}\cos{\beta}}\\<br />\dfrac{1}{\sin{\beta}\cos{\beta}}&= \dfrac{1}{\sin{\beta}\cos{\beta}} \ \blacksquare\\<br />\end{aligned}\end{equation}$ No se como evaluan este tipo de demostraciones, pero la idea es llegar desde un lado para el otro, ''sin tocar'' un lado de la igualdad. Es un par de pasos mas solamente. Saludos -------------------- USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan ----------------- CURRICULUM VITAE ----------------- 296 pts en la PSU de Matemáticas Admisión 2010. Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica U. de Talca VII Region Chile

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 28 2007, 10:14 PM Publicado: #9
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(XaPi @ Dec 29 2007, 12:46 AM) No se como evaluan este tipo de demostraciones, pero la idea es llegar desde un lado para el otro, ''sin tocar'' un lado de la igualdad. Es un par de pasos mas solamente. Saludos Ah, yo tenía entendido que mientras no se hicieran pasos que involucraban que la igualdad era una igualdad, debido a que era lo que se keria demostrar, todo valía xD. -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Pily Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 29 2007, 10:28 PM Publicado: #10
Dios Matemático Grupo: Usuario FMAT Mensajes: 365 Registrado: 27-May 05 Desde: Puente Asalto, Santiago Miembro Nº: 68 Nacionalidad: Colegio/Liceo: Sexo:	CITA(Abu-Khalil @ Dec 29 2007, 12:14 AM) Ah, yo tenía entendido que mientras no se hicieran pasos que involucraban que la igualdad era una igualdad, debido a que era lo que se keria demostrar, todo valía xD. La idea, como dice Xapi, es llegar de un lado hacia el otro... ahora, como "truco" de repente se usa que si por ejemplo comienzas a desarrollar la parte izquierda y llegas a una expresión "A" sin saber qué más hacer, tomas el lado derecho y tratas de llegar a esa misma expresión "A" y luego haces un copy-paste [de atrás hacia adelante] en la parte izquierda (asegurándote que cada paso sea revertible, obviamente). --------------------

« Posterior · Geometría · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 10th April 2025 - 11:51 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.