|
|
|
|
|
|
|
  |
 Dec 13 2007, 09:16 PM Dec 13 2007, 09:16 PM
Publicado:
#1
|
|
 Maestro Matemático Grupo: Usuario FMAT Mensajes: 119 Registrado: 1-June 07 Desde: Santiago Miembro Nº: 6.347 Nacionalidad:  Colegio/Liceo:  Sexo:  |
![TEX: Si $f:[a,b] \rightarrow \mathbb{R}$ es una funcion definida tal que $f(x)=0$, excepto para $x \in \{c_1,...,c_n\} \subset [a,b]$. Pruebe que $f$ es integrable y calcule su integral](./tex/71081a91c77cb4c2fc96c943232402c6.gif) 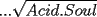
|
|
|
|
 Dec 18 2007, 12:33 PM Dec 18 2007, 12:33 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Colaborador Gold Mensajes: 874 Registrado: 18-October 07 Desde: The Matrix... Miembro Nº: 11.478 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
![TEX: Si $f:[a,b] \rightarrow \mathbb{R}$ es una funcion definida tal que $f(x)=0$, excepto para $x \in \{c_1,...,c_n\} \subset [a,b]$. Pruebe que $f$ es integrable y calcule su integral](./tex/71081a91c77cb4c2fc96c943232402c6.gif) 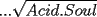 Se define una partición del intervalo [a,b]. El ancho de estos intervalos da lo mismo, pero supondré (por simplicidad) que son todos iguales a ![TEX: \[<br />\Delta x = \frac{{b - a}}<br />{n}<br />\]](./tex/d9ed7527d5109ce83f4e9d9b5dcb4ccc.gif) . .Dentro de cada uno de los subintervalos que se forman, podrá o no haber alguno de los valores ![TEX: \[c_n\]](./tex/ddf3ad8e61ccefc9ce44a6095ceed147.gif) . Para el k-ésimo de estos "intervalitos", sea . Para el k-ésimo de estos "intervalitos", sea ![TEX: \[x_k\]](./tex/cc646e0b4cb2fd3ee36f60cf70cf200a.gif) el valor que genera el máximo valor de f(x). el valor que genera el máximo valor de f(x).Ahora, para verificar la integrabilidad, hay que calcular las sumas superior e inferior de Riemann, y verificar que convergen al mismo valor. Calculemos la suma superior: ![TEX: \[<br />S = f\left( {x_1 } \right)\Delta x + f\left( {x_2 } \right)\Delta x + \ldots + f\left( {x_n } \right)\Delta x = \left[ {f\left( {x_1 } \right) + f\left( {x_2 } \right) + \ldots + f\left( {x_n } \right)} \right]\Delta x<br />\]](./tex/9cde216112543ccff567f2a38627fe96.gif) luego, ![TEX: \[<br />\mathop {\lim }\limits_{\Delta x \to 0} S = \mathop {\lim }\limits_{\Delta x \to 0} \left[ {f\left( {x_1 } \right) + f\left( {x_2 } \right) + \ldots + f\left( {x_n } \right)} \right]\Delta x = 0<br />\]](./tex/9944499329652ea16aa11d639308836c.gif) La suma inferior, por su parte, es evidentemente idéntica a cero, pues el valor que minimiza la función dentro de cada subintervalo es cualquiera distinto de los puntos ![TEX: \[c_n\]](./tex/3d86c160acd4acb3a6fc187daea0c66f.gif) , y así el valor de f(x) para la suma inferior es siempre igual a cero. , y así el valor de f(x) para la suma inferior es siempre igual a cero.Luego, como las sumas superior e inferior convergen al mismo valor, la función es integrable y ![TEX: \[<br />\int\limits_a^b {f\left( x \right)dx} = \mathop {\lim }\limits_{\Delta x \to 0} S = \mathop {\lim }\limits_{\Delta x \to 0} s = 0<br />\]](./tex/e7ad9d8bf8d53dfc4339a33ac6a6a6a2.gif)
-------------------- |
|
|
|
 Dec 21 2007, 11:56 PM Dec 21 2007, 11:56 PM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
Se puede tomar este problema con teoria de la medida y la integral de lebesque ...solo ver que
![TEX: $\mu ([a,b]\cap \{ c_1, ..., c_n \} )=\mu (\{ c_1, ..., c_n \})=0$](./tex/d6c91465fdec8c8896119a53af85167f.png) y se llega a lo mismo y se llega a lo mismosaludos |
|
|
|
 Apr 5 2008, 11:38 AM Apr 5 2008, 11:38 AM
Publicado:
#4
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
ESTO TAMBIEN PUEDE RESPONDERSE USANDO UN ARGUMENTO DE DIMENSIONALIDAD, LA INTEGRAL COMO MIDE AREAS, AL HACER SUMA DE RIEMANN, ES OBIO QUE LA SUMA DA CERO, YA QUE LOS PUNTOS DADOS NO TIENEN DIMENSION, DE MODO QUE UN PUNTO EN EL ESPACIO NO TIENE PERIMETRO, NI AREA, NI VOLUMEN, ES SOLO UN PUNTO, SIN EMBARGO ES INTEGRABLE A MENOS QUE EN ALGUNOS DE LOS PUNTOS SE COMPORTE COMO UNA DELTA DE DIRAC, EN ESTE CASO LA INTEGRAL SERIA DE ALMENOS 1 O -1 SEGUN MCOMO VAYA DIRECCIONADO LA DELTA NOTAR QUE F NO ES CONTINUA, Y SIN EMBARGO AMENOS QUE 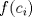 sea FINITA LA INTEGRAL ES CERO, sea FINITA LA INTEGRAL ES CERO, ESOP SALUDOOOS CLAUDIO -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
 May 26 2015, 11:26 AM May 26 2015, 11:26 AM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
ESTO TAMBIEN PUEDE RESPONDERSE USANDO UN ARGUMENTO DE DIMENSIONALIDAD, LA INTEGRAL COMO MIDE AREAS, AL HACER SUMA DE RIEMANN, ES OBIO QUE LA SUMA DA CERO, YA QUE LOS PUNTOS DADOS NO TIENEN DIMENSION, DE MODO QUE UN PUNTO EN EL ESPACIO NO TIENE PERIMETRO, NI AREA, NI VOLUMEN, ES SOLO UN PUNTO, SIN EMBARGO ES INTEGRABLE A MENOS QUE EN ALGUNOS DE LOS PUNTOS SE COMPORTE COMO UNA DELTA DE DIRAC, EN ESTE CASO LA INTEGRAL SERIA DE ALMENOS 1 O -1 SEGUN MCOMO VAYA DIRECCIONADO LA DELTA NOTAR QUE F NO ES CONTINUA, Y SIN EMBARGO AMENOS QUE 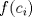 sea FINITA LA INTEGRAL ES CERO, sea FINITA LA INTEGRAL ES CERO, ESOP SALUDOOOS CLAUDIO Parece que ud. no leyo el post del finado jorgeston señor "e" de hace 7 años. ¿Porque menciono la delta de dirac? que tiene que ver? Estoy perdiendo el tiempo con "ud" en el cual deberia estar estudiando para la interrogacion de metodos estadisticos dictado por el señor Manuel Galea. Todo es facil si se estudia el recorrido en vez del dominio, esta manera es mucho mas efectiva que la particion usual de riemann ya que se utiliza el concepto de medida, el cual obviamente no sabe. Sin embargo estoy de acuerdo en que no existe especificacion de cuanto debiese valer la funcion en los puntos señalados, solo señala "excepto", pero ello no me dice nada. Perfectamente puede explotar en algun punto de los mencionados. Ud menciono la delta de dirac, pero no formulo bien su argumento. Ademas, me parece muy molesto para la vista que haya escrito con letras mayusculas, el amo y señor Kenshin le regañara por que parece que estuviera gritando y le suspendera por 24 horas. Ud. Deberia poner mas atencion a los ramos de analisis, por que le servirá en el futuro y poner menos atencion a meiko rokudo y dejar de llorar por su amiga tamy. No merece ni un saludo, me voy, indignadisimo. PD: pu'ta que cansa hablar como coquitao w'n. PD2: Catolica por siempre PD3: volvi a autocorregirme. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 11:02 PM |