I3 Cálculo II - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad Católica > Cálculo II

Reply to this topic

Start new topic

I3 Cálculo II, MAT1512 2S 2007

EnnaFrad Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 10 2007, 01:36 PM Publicado: #1
Maestro Matemático Grupo: Usuario FMAT Mensajes: 121 Registrado: 6-December 05 Desde: Las Condes - Chillán Miembro Nº: 460 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />$ $ \\<br />MAT1512 - INTERROGACI\'ON 3 \\<br />12 de Noviembre de 2007 \\<br />$ $ \\<br />$\boxed{1}$ Estudie la convergencia de las siguientes series num\'ericas: \\<br />a) $\displaystyle\sum\limits_{n=0}^\infty \dfrac{2^n-n}{3^n+n}$ \\<br />b) $\displaystyle\sum\limits_{n=1}^\infty {(-1)^n}{(\log(n+1) - \log{n})}$<br />$ $ \\<br />$\boxed{2}$ Estudie la convergencia de las siguientes integrales impropias: \\<br />a) $\displaystyle\int\limits_0^1 \dfrac{dx}{\sqrt{x} (1-x)}$ \\<br />b) $\displaystyle\int\limits_0^1 \dfrac{dx}{e^{\sqrt{x}}-\cos{x}}$ \\<br />$ $ \\<br />$\boxed{3}$ \\<br />a) Calcule el valor exacto de $\displaystyle\sum\limits_{n=0}^\infty \dfrac{(-1)^n}{2n+1}$. Justifique su respuesta. \\<br />b) Sean $a$,$b$ n\'umeros reales positivos. Se construye la siguiente serie: \\<br />$1+a+ab+a^2 b+ a^2 b^2 + a^3 b^2 + a^3 b^3 + a^4 b^3 + a^4 b^4 + ...$ \\<br /> Determine todos los valores de $a$ y $b$ de manera que la serie sea convergente. \\<br /> $ $ \\<br /> $\boxed{4}$ Considere la funci\'on $g(x) = \dfrac{9x}{x^2-4x+13}$. \\<br /> a) Represente a $g$ como una serie de potencias en torno a $x=2$. \\<br /> b) Determine los valores de $x$ donde la representaci\'on de $g$ es v\'alida.\\<br />$ Mensaje modificado por EnnaFrad el Dec 10 2007, 01:43 PM

EnnaFrad Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 10 2007, 01:43 PM Publicado: #2
Maestro Matemático Grupo: Usuario FMAT Mensajes: 121 Registrado: 6-December 05 Desde: Las Condes - Chillán Miembro Nº: 460 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Ahora si... perdón por la tardanza, ahora me pondré al día. Saludos y respondan la I3

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 10 2008, 10:59 PM Publicado: #3
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> b)S_n = \sum\limits_{n = 1}^\infty {\left( { - 1} \right)^n \left( {\log (n + 1) - \log (n)} \right)} \hfill \\<br /> \hfill \\<br /> \Rightarrow S_{n1} = \sum\limits_{n = 1}^\infty {\left\| {\log (n + 1) - \log (n)} \right\|} = \sum\limits_{n = 1}^\infty {\left\| {\log \left( {1 + \frac{1}<br />{n}} \right)} \right\|} \hfill \\<br /> \hfill \\<br /> {\text{Sea }}a_n = \log \left( {1 + \frac{1}<br />{n}} \right) \Rightarrow a_n \leqslant 2{\text{ y ademas }}a_n {\text{ es decreciente}} \Rightarrow S_{n1} {\text{ converge }} \Leftrightarrow S_n \hfill \\<br /> {\text{tambien converge}} \hfill \\ <br />\end{gathered} <br />\]<br />$ aunque probar la convergencia de esta serie, es trival aplicando Leibniz -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 11 2008, 08:20 PM Publicado: #4
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> a)S = \sum\limits_{n = 0}^\infty {\frac{{2^n - n}}<br />{{3^n + n}} < } \sum\limits_{n = 0}^\infty {\frac{{2^n - n}}<br />{{3^n }}} = \sum\limits_{n = 0}^\infty {\left( {\frac{2}<br />{3}} \right)^n - \frac{n}<br />{{3^n }}} \hfill \\<br /> \hfill \\<br /> {\text{Es claro que }}\left( {\frac{2}<br />{3}} \right)^n {\text{ converge}}{\text{, el resto tambien}}{\text{, pero si no es tan evidente:}} \hfill \\<br /> a_n = \frac{n}<br />{{3^n }} \Rightarrow \mathop {\lim }\limits_{n \to \infty } \frac{{a_{n + 1} }}<br />{{a_n }} = \mathop {\lim }\limits_{n \to \infty } \frac{{n + 1}}<br />{{3^n \cdot 3}} \cdot \frac{{3^n }}<br />{n} = \frac{1}<br />{3} < 1 \Rightarrow a_n {\text{ coverge}} \hfill \\<br /> \hfill \\<br /> \therefore \sum\limits_{n = 0}^\infty {\left( {\frac{2}<br />{3}} \right)^n - \frac{n}<br />{{3^n }}} {\text{ converge}} \Rightarrow S{\text{ converge}} \hfill \\ <br />\end{gathered} <br />\]<br />$ -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

DressedToKill Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 11 2008, 09:20 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.818 Registrado: 21-December 06 Miembro Nº: 3.434	CITA(naxoobkn @ Oct 11 2008, 09:10 PM) $TEX: \[<br />\begin{gathered}<br /> a)S = \sum\limits_{n = 0}^\infty {\frac{{2^n - n}}<br />{{3^n + n}} < } \sum\limits_{n = 0}^\infty {\frac{{2^n - n}}<br />{{3^n }}} = \sum\limits_{n = 0}^\infty {\left( {\frac{2}<br />{3}} \right)^n - \frac{n}<br />{{3^n }}} \hfill \\<br /> \hfill \\<br /> {\text{Es claro que }}\left( {\frac{2}<br />{3}} \right)^n {\text{ converge}}{\text{, el resto tambien}}{\text{, pero si no es tan evidente:}} \hfill \\<br /> a_n = \frac{n}<br />{{3^n }} \Rightarrow \mathop {\lim }\limits_{n \to \infty } \frac{{a_{n + 1} }}<br />{{a_n }} = \mathop {\lim }\limits_{n \to \infty } \frac{{n + 1}}<br />{{3^n \cdot 3}} \cdot \frac{{3^n }}<br />{n} = \frac{1}<br />{3} < 1 \Rightarrow a_n {\text{ coverge}} \hfill \\<br /> \hfill \\<br /> \therefore \sum\limits_{n = 0}^\infty {\left( {\frac{2}<br />{3}} \right)^n - \frac{n}<br />{{3^n }}} {\text{ converge}} \Rightarrow S{\text{ converge}} \hfill \\ <br />\end{gathered} <br />\]<br />$ Del primer paso pudiste haber notado que 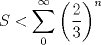$TEX: $S < \displaystyle\sum_0^{\infty} \left(\dfrac{2}{3}\right)^n$$ Y ahí concluyes rápido. -------------------- http://www.youtube.com/watch?v=sp_WV91jx8E...feature=related

Naxoo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 12 2008, 01:51 PM Publicado: #6
Staff FMAT Grupo: Moderador Mensajes: 2.604 Registrado: 2-March 07 Desde: Somewhere over the rainbow Miembro Nº: 4.244 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(DressedToKill @ Oct 11 2008, 10:10 PM) Del primer paso pudiste haber notado que 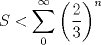$TEX: $S < \displaystyle\sum_0^{\infty} \left(\dfrac{2}{3}\right)^n$$ Y ahí concluyes rápido. tienes razon xD aca va la 3.a) $TEX: \[<br />\begin{gathered}<br /> \sum\limits_{n = 0}^\infty {\left( { - x^2 } \right)^n } = \sum\limits_{n = 0}^\infty {\left( { - 1} \right)^n x^{2n} } = \frac{1}<br />{{1 + x^2 }}\forall x \in \left( { - 1,1} \right) \hfill \\<br /> {\text{Sea }}f:\left( { - 1,1} \right) \to \mathbb{R}{\text{ definida por }}f(x) = \frac{1}<br />{{1 + x^2 }} = \sum\limits_{n = 0}^\infty {\left( { - 1} \right)^n x^{2n} } \hfill \\<br /> \Rightarrow \int {\sum\limits_{n = 0}^\infty {\left( { - 1} \right)^n x^{2n} } } dx = \sum\limits_{n = 0}^\infty {\frac{{\left( { - 1} \right)^n x^{2n + 1} }}<br />{{2n + 1}}} + C \hfill \\<br /> \hfill \\<br /> {\text{Pero la funcion cuta derivada es }}f{\text{ corresponde al arctangente}} \hfill \\<br /> {\text{Sea }}F:\left( { - 1,1} \right) \to \mathbb{R}{\text{ definida por }}F(x) = \arctan (x) = \sum\limits_{n = 0}^\infty {\frac{{\left( { - 1} \right)^n x^{2n + 1} }}<br />{{2n + 1}}} + C \hfill \\<br /> F(0) = \arctan (0) = \sum\limits_{n = 0}^\infty {\frac{{\left( { - 1} \right)^n 0^{2n + 1} }}<br />{{2n + 1}}} + C \Rightarrow C = 0 \hfill \\<br /> \hfill \\<br /> \therefore F(x) = \sum\limits_{n = 0}^\infty {\frac{{\left( { - 1} \right)^n x^{2n + 1} }}<br />{{2n + 1}}} = \arctan (x) \Rightarrow F(1) = \arctan (1) = \boxed{\sum\limits_{n = 0}^\infty {\frac{{\left( { - 1} \right)^n }}<br />{{2n + 1}} = } \frac{\pi }<br />{4}} \hfill \\ <br />\end{gathered} <br />\]<br />$ me gusta esta materia -------------------- INRIA - Francia, Sophia Antipolis Biocore Team Ingeniero Civil en Biotecnología Ingeniería Civil Químico “(…) los elementos que él (¿o Él?) [Dios] mismo nos ha dado (raciocinio, sensibilidad, intuición) no son en absoluto suficientes como para garantizarnos ni su existencia ni su no existencia. Gracias a una corazonada puedo creer en Dios y acertar o no creer en Dios y también acertar" Mario Benedetti $TEX: \[\iiint\limits_\Omega {\left( {\nabla \cdot \vec F} \right)dV} = \iint\limits_{\partial \Omega } {\left( {\vec F \cdot \hat n} \right)}dS\]<br />$

khuzdul Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 25 2008, 02:11 PM Publicado: #7
Dios Matemático Grupo: Usuario FMAT Mensajes: 404 Registrado: 1-October 07 Desde: Santiago Miembro Nº: 10.782 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	2.a) $TEX: \[<br />\int_0^1 {\frac{{dx}}{{\sqrt x \left( {1 - x} \right)}}} <br />\]<br />$ Tenemos que tanto 0 como 1 son singularidad, es decir,la función se dispara al infinito en estos puntos. Por eso separaremos la integral de la siguiente manera: $TEX: <br />\[<br />\int_0^1 {\frac{{dx}}{{\sqrt x \left( {1 - x} \right)}}} = \underbrace {\int_0^{1/2} {\frac{{dx}}{{\sqrt x \left( {1 - x} \right)}}} }_{I1} + \underbrace {\int_{1/2}^1 {\frac{{dx}}{{\sqrt x \left( {1 - x} \right)}}} }_{I2}<br />\]<br />$ Analizaremos la convergencia de I1 y de I2, si alguna de las dos diverge la integral original diverge Para I1 se tiene $TEX: <br />\[<br />f(x) = \frac{1}{{\sqrt x \left( {1 - x} \right)}}<br />\]$ Sea $TEX: \[<br />{\rm{g(x) = }}\frac{1}{{\sqrt x }}<br />\]$ , $TEX: \[<br />\int_0^1 {\frac{{dx}}{{\sqrt x }}} <br />\]<br />$ Converge, pues $TEX: \[<br />{\rm{1/2 < 1}}{\rm{.}}<br />\]<br />$ Luego $TEX: <br />\[<br />{\rm{L = }}\mathop {\lim }\limits_{x \to 0^ + } \frac{{f(x)}}{{g(x)}} = \mathop {\lim }\limits_{x \to 0^ + } \frac{{\frac{1}{{\sqrt x \left( {1 - x} \right)}}}}{{\frac{1}{{\sqrt x }}}} = \mathop {\lim }\limits_{x \to 0^ + } \frac{1}{{\left( {1 - x} \right)}} = 1<br />\]$ L es finito por lo que I1 converge Para I2 $TEX: \[<br />f(x) = \frac{1}{{\sqrt x \left( {1 - x} \right)}}<br />\]$ Sea $TEX: \[<br />{\rm{g(x) = }}\frac{1}{{\left( {1 - x} \right)}}<br />\]<br /><br />$ , $TEX: \[<br />\int_1^{1/2} {\frac{{dx}}{{\left( {1 - x} \right)}}} <br />\]<br />$ Diverge pues, el exponente de $TEX: \[<br />1 - x<br />\]$ es 1. Luego. $TEX: <br />\[<br />{\rm{L = }}\mathop {\lim }\limits_{x \to 0^ + } \frac{{\frac{1}{{\sqrt x \left( {1 - x} \right)}}}}{{\frac{1}{{\left( {1 - x} \right)}}}} = \mathop {\lim }\limits_{x \to 0^ + } \frac{1}{{\sqrt x }} = 1<br />\]<br />$ Como L es finito se tiene que I2 diverge. Concluimos finalmente que $TEX: \[<br />\int_0^1 {\frac{{dx}}{{\sqrt x \left( {1 - x} \right)}}} <br />\]$ diverge Mensaje modificado por khuzdul el Oct 25 2008, 02:35 PM -------------------- $TEX: % MathType!MTEF!2!1!+-<br />% feaaguart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGcbaGaamOuamaaBa<br />% aaleaacqaH8oqBcqaH9oGBaeqaaOGaeyOeI0YaaSaaaeaacaaIXaaa<br />% baGaaGOmaaaacaWGNbWaaSbaaSqaaiabeY7aTjabe27aUbqabaGcca<br />% WGsbGaey4kaSIaam4zamaaBaaaleaacqaH8oqBcqaH9oGBaeqaaOGa<br />% eu4MdWKaeyypa0ZaaSaaaeaacaaI4aGaeqiWdaNaam4raaqaaiaado<br />% gadaahaaWcbeqaaiaaisdaaaaaaOGaamivamaaBaaaleaacqaH8oqB<br />% cqaH9oGBaeqaaaaa!53E0!<br />\[{R_{\mu \nu }} - \frac{1}<br />{2}{g_{\mu \nu }}R + {g_{\mu \nu }}\Lambda = \frac{{8\pi G}}<br />{{{c^4}}}{T_{\mu \nu }}\]<br />$

« Posterior · Cálculo II · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 17th April 2025 - 04:59 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.