|
|
|
|
|
|
|
  |
 Dec 8 2007, 05:41 PM Dec 8 2007, 05:41 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
 P y Q son puntos externos a esa circunferencia, de las cuales se trazan unas secantes hacia el circulo tan que forman el cuadrilatero ABCD. Luego se trazan las bisectrices PX y QY. Probar que PX es perpendicular a QY. Con 2 formas distintas estamos pasando a resueltos =D salu2 --------------------  |
|
|
|
 Feb 8 2008, 09:06 PM Feb 8 2008, 09:06 PM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Solucion :
 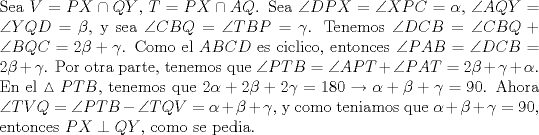
Mensaje modificado por Felipe_ambuli el Feb 10 2008, 02:33 PM |
|
|
|
 Feb 8 2008, 10:48 PM Feb 8 2008, 10:48 PM
Publicado:
#3
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Solucion : 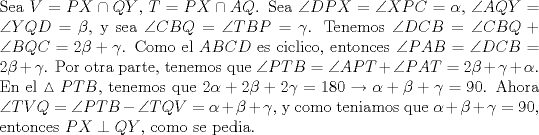 Tu solución es correcta, aunque falta la figura 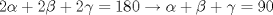 ", debería decir "en el triángulo PAB..."). Como pelao pide dos soluciones distintas, este problema sigue en la sección de propuestos. ", debería decir "en el triángulo PAB..."). Como pelao pide dos soluciones distintas, este problema sigue en la sección de propuestos.Saludos -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
 Feb 9 2008, 12:50 PM Feb 9 2008, 12:50 PM
Publicado:
#4
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 45 Registrado: 20-October 07 Miembro Nº: 11.559 Nacionalidad:  Sexo:  |
![TEX: \begin{minipage}{0.1<br />\textwidth}\psshadowbox[linecolor=Black,framearc=0.5,linewidth=0.5pt,fillstyle=gradient,gradbegin=Blue,grad<br />end=white,framesep=4pt,shadowcolor=Black,gradmidpoint=0.9]<br />{Solución}\\[1cm]\end{minipage}](./tex/10557c39d265d983d0b798bc44d755f1.png)  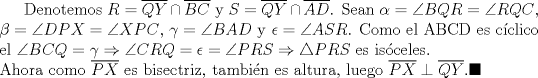
|
|
|
|
 Feb 10 2008, 02:40 PM Feb 10 2008, 02:40 PM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 836 Registrado: 9-January 07 Desde: Santiasko Miembro Nº: 3.659 Nacionalidad:  Sexo:  |
Killua pero en el triangulo PTB tbn se cumple que
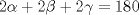 Ah y lo de la imagen no pude ponerla en el post anterior pq no podia subirla a imageshack Saludos |
|
|
|
 Feb 10 2008, 11:33 PM Feb 10 2008, 11:33 PM
Publicado:
#6
|
|
 Staff Fmat Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
Killua pero en el triangulo PTB tbn se cumple que 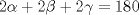 Ah y lo de la imagen no pude ponerla en el post anterior pq no podia subirla a imageshack Saludos Toda la razón, me confundí ya que no tenías figura ![TEX: \begin{minipage}{0.1<br />\textwidth}\psshadowbox[linecolor=Black,framearc=0.5,linewidth=0.5pt,fillstyle=gradient,gradbegin=Blue,grad<br />end=white,framesep=4pt,shadowcolor=Black,gradmidpoint=0.9]<br />{Solución}\\[1cm]\end{minipage}](./tex/10557c39d265d983d0b798bc44d755f1.png)  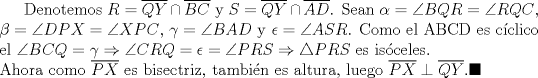 La solución es correcta, pero creo que te saltaste un paso, cuando concluyes que 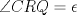 . Notar que viene dado por la suma de los ángulos en el triángulo ASQ ( . Notar que viene dado por la suma de los ángulos en el triángulo ASQ (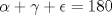 ) y en el triángulo CRQ tenemos ) y en el triángulo CRQ tenemos 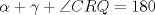 . .Con dos soluciones básicamente distintas, pasamos a resueltos Saludos. -------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 17th October 2025 - 04:17 AM |










