Una Novedosa - Foro fmat.cl

Una Novedosa, Resuelta por Zeus

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 25 2006, 12:50 AM Publicado: #1
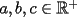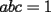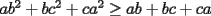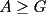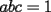Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	Problema Sean $TEX: $a,b,c\in\mathbb{R}^+$$ tales que $TEX: $abc=1$$ Probar que: $TEX: $ab^2+bc^2+ca^2\ge ab+bc+ca$$ Solucion: Por desigualdad $TEX: $A\ge G$$ y por el enunciado que dice que $TEX: $abc =1$$ , tenemos que: $TEX: $\frac{\displaystyle{ab^2 + bc^2 + bc^2}}{\displaystyle{3}}\ge \sqrt[3]{ab^4c^4} = bc \sqrt[3]{abc} = bc$$ .................................................................................................... ........................... $TEX: $\frac{\displaystyle{bc^2 + ca^2 + ca^2}}{\displaystyle{3}}\ge \sqrt[3]{bc^4a^4} = ac \sqrt[3]{abc} = ac$$ .................................................................................................... ........................... $TEX: $\frac{\displaystyle{ca^2 + ab^2 + ab^2}}{\displaystyle{3}}\ge \sqrt[3]{ca^4b^4} = ab \sqrt[3]{abc} = ab$$ Sumando las tres desigualdades tenemos que: 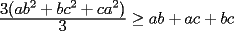$TEX: $\frac{\displaystyle{3 (ab^2 + bc^2 + ca^2)}}{\displaystyle{3}}\ge ab + ac + bc$$ Problema solucionado! Resuelto por Zeus -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)