Identificarse Registrarse

Psu
Enseñanza Básica
Enseñanza Media
Universidad
Olimpiadas
Comunidad



 
 Reply to this topicStart new topic
> calculo vectorial, medio
imog
mensaje Nov 26 2007, 02:48 PM
Publicado: #1


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 4
Registrado: 17-October 07
Miembro Nº: 11.441
Nacionalidad:
Sexo:



Si f(x)≤f(a) para todo x de B(a) de mostrar que el gradf(a)=0,suponiendo que f es diferenciable en toda n-bola B(a). donde B(a) es una bola centrada en a
att:imog, salu2

Mensaje modificado por imog el Aug 21 2008, 05:53 PM
Go to the top of the page
 
+Quote Post
Jorgeston
mensaje Dec 1 2007, 05:53 PM
Publicado: #2


Dios Matemático Supremo


Grupo: Baneado
Mensajes: 2.588
Registrado: 7-November 06
Miembro Nº: 2.747
No entiendo la bola B(a)...es una bola abierta centrada en a? centrada en x? de radio a y centro x? al reves?


por favor sé mas claro,..asi no se puede empezar una demostracion


salu2

Mensaje modificado por jorgeston el Dec 1 2007, 05:53 PM
Go to the top of the page
 
+Quote Post
XaPi
mensaje Dec 1 2007, 05:55 PM
Publicado: #3


Dios Matemático Supremo
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 1.872
Registrado: 9-March 06
Desde: Welcome
Miembro Nº: 614
Nacionalidad:
Colegio/Liceo: Liceo Jose Victorino Lastarria
Universidad: Universidad de Talca
Sexo:



es una bola centrada en a...

y x es un elemento de la bola.


--------------------
USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan

-----------------
CURRICULUM VITAE
-----------------

296 pts en la PSU de Matemáticas Admisión 2010.

Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica
U. de Talca
VII Region
Chile
Go to the top of the page
 
+Quote Post
Jorgeston
mensaje Dec 1 2007, 06:20 PM
Publicado: #4


Dios Matemático Supremo


Grupo: Baneado
Mensajes: 2.588
Registrado: 7-November 06
Miembro Nº: 2.747
A ver, he salido de la practica en lo que se refiere a calculo 3 xD. pero se me ocurrio algo..

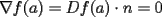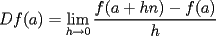Solo basta notar que TEX: $\nabla f(a)=Df(a)\cdot n=0$ puesto que TEX: $$Df(a)=\lim_{h\to 0}\frac{f(a+hn)-f(a)}{h}$$ es cero

esto se demuestra usando teorema del sandwich en el limite...

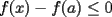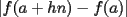como TEX: $f(x)- f(a)\leq 0$ para todo elemento TEX: $x$ de una bola centrada en TEX: $a$ en tenemos que TEX: $|f(a+hn)-f(a)|$ es menor que cero, en especial si h se va a cero...es la idea intuitiva de lo que pasa en la vecindad de TEX: $a$

salu2

Mensaje modificado por jorgeston el Dec 1 2007, 06:26 PM
Go to the top of the page
 
+Quote Post
imog
mensaje Aug 21 2008, 05:50 PM
Publicado: #5


Principiante Matemático
Ícono de Grupo

Grupo: Usuario FMAT
Mensajes: 4
Registrado: 17-October 07
Miembro Nº: 11.441
Nacionalidad:
Sexo:



CITA(jorgeston @ Dec 1 2007, 06:43 PM) *
No entiendo la bola B(a)...es una bola abierta centrada en a? centrada en x? de radio a y centro x? al reves?
por favor sé mas claro,..asi no se puede empezar una demostracion
salu2


es una bola centrada en a y x pertenece a la bola.
att:imog, salu2
Go to the top of the page
 
+Quote Post
 

Reply to this topicStart new topic
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):

 

Versión Lo-Fi Fecha y Hora actual: 23rd November 2024 - 08:12 PM
Powered By IP.Board 2.2.1 © 2007  IPS, Inc.