 Otro problema, Resuelto por pelao_malo |
|
|
|
|
|
|
  |
 Nov 17 2007, 04:25 PM
Publicado:
#1
|
|
|
Doctor en Matemáticas  Grupo: Usuario FMAT Mensajes: 170 Registrado: 25-July 07 Miembro Nº: 7.812  |
Probar que en un grupo de n personas
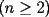 , siempre hay a lo menos 2 que tienen el mismo número de amigos dentro del grupo
|
 |
 
|
|
Nov 17 2007, 08:56 PM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad:  Colegio/Liceo:  Sexo:  |
una persona puede tener a lo mas n-1 amigos, ya que no puede ser amigo de si misma. Asi todas las personas tendran n-1,n-2,n-3,...,2,1,0 amigos. Son n amigos para n personas. pero hay que observar que una persona no puede tener 0 amigos y otra n-1 amigos, ya que esta ultima considera amigo al primero, el cual no tiene amigos. entonces hay n-1 amigos a elegir entre n personas, por lo que si cada persona tiene una cantidad distinta, la n-esima tendra algun amigo ya amigado xD y ese duo sera el que demuestre el problema.
Mensaje modificado por pelao_malo el Nov 17 2007, 08:56 PM --------------------  |
|
|
|
|
Nov 17 2007, 11:12 PM
Publicado:
#3
|
|
 Staff Fmat  Grupo: Moderador Mensajes: 1.185 Registrado: 29-October 05 Desde: Santiago, Chile Miembro Nº: 352 Nacionalidad: Colegio/Liceo:  Universidad:  Sexo: |
La solución de pelao_malo es correcta. Agregar que este es un problema clásico de olimpíadas nacionales. Moviendo a la sección correspondiente (problemas resueltos sector "otros")
Saludos 
-------------------- "He looks rather ill, but he looks all over the genius he was" (G. H. Hardy)
"A mathematician is a device for turning coffee into theorems" (Paul Erdös) |
|
|
|
|
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 23rd November 2024 - 04:21 PM |
