Un sistema y algo de paciencia - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector PreOlímpico > Álgebra > Problemas Propuestos

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Un sistema y algo de paciencia, [basico]

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 12 2006, 11:16 PM Publicado: #1
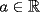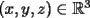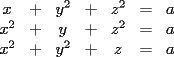Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Para cada $TEX: $a\in\mathbb{R}$$ , determine el número de soluciones $TEX: $(x,y,z)\in\mathbb{R}^3$$ del siguiente sistema de ecuaciones: $TEX: <br />$\begin{array}{ccccccc}<br />x & + & y^2 & + & z^2 & = & a \\<br />x^2 & + & y & + & z^2 & = & a \\<br />x^2 & + & y^2 & + & z & = & a<br />\end{array}$<br />$ Fuente: Polonia, ronda 2, año 1997 -------------------- Sebastián Elías Puelma Moya Administrador FMAT

DQA Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 10 2006, 02:59 PM Publicado: #2
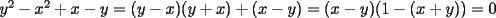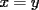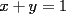Matemático Grupo: Usuario FMAT Mensajes: 44 Registrado: 4-December 05 Desde: Talcahuano Miembro Nº: 451	no entendi lo del enunciado (de que pertencen a los reales al cubo) pero aca va mi solucion del sistema. se toman dos ecuaciones cualquiera y se restan, por ejemplo (1) y (2) $TEX: $y^2 - x^2 + x - y = (y-x)(y+x) + (x-y) = (x - y)(1 - (x+y)) = 0$$ hay dos posibilidades, $TEX: $x=y$$ o $TEX: $x+y = 1$$ . 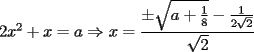en el primer caso dada la simetria del sistema todas las incognitas son iguales, entonces el problema se reduciria a despejar la incognita en una ecuacion de la forma $TEX: $2x^2 + x = a \Rightarrow{x = \displaystyle{\frac{\pm{\sqrt{a + \frac{1}{8}}} - \frac{1}{2\sqrt{2}}}{\sqrt{2}}}}$$ en el segundo caso se toman, por ejem, (2) y (3) y se suman 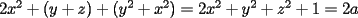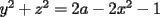$TEX: $2x^2 + (y + z) + (y^2 + x^2) = 2x^2 + y^2 + z^2 + 1 = 2a$$ $TEX: $y^2 + z^2 = 2a - 2x^2 - 1$$ reemplazando en la primera ecuacion queda que las soluciones son de la forma 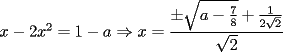$TEX: $ x - 2x^2 = 1 - a\Rightarrow{x = \displaystyle{\frac{\pm{\sqrt{a - \frac{7}{8}}} + \frac{1}{2\sqrt{2}}}{\sqrt{2}}}}$$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 10 2006, 07:27 PM Publicado: #3
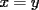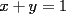Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	CITA(DQA @ Feb 10 2006, 04:59 PM) no entendi lo del enunciado (de que pertencen a los reales al cubo). ... hay dos posibilidades, $TEX: $x=y$$ o $TEX: $x+y = 1$$ . en el primer caso dada la simetria del sistema todas las incognitas son iguales... La solución está incorrecta... necesitas ser un poco más oriental, o sea tener algo más de paciencia. A continuación te explico un poco mejor de qué estoy hablando: Cuando escribo " 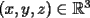$TEX: $(x,y,z)\in\mathbb{R}^3$$ ", quiero decir solamente que las tres incógnitas han de ser reales. Es solamente eso: cuando tomo tres números reales, la terna de ellos esta en la tercera potencia cartesiana. Lo que puse después, es donde cometiste el primer error. No puedes decir que forzosamente las tres incógnitas deben ser iguales, en el caso 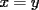$TEX: $x=y$$ . Puedes notar que la incógnita $TEX: $z$$ puede ser diferente. Cuando llegas a una ecuación cuadrática, como 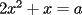$TEX: $2x^2+x=a$$ , el hecho que las incógnitas sean reales, da información sobre los posibles valores de $TEX: $a$$ Y bueno, por esto es evidente que el problema sigue pendiente de respuesta, y no hablo más para no seguir dándoles pistas -------------------- Sebastián Elías Puelma Moya Administrador FMAT

picosenotheta Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 11 2006, 04:15 AM Publicado: #4
Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(xsebastian @ Jan 12 2006, 11:16 PM) Para cada $TEX: $a\in\mathbb{R}$$ , determine el número de soluciones $TEX: $(x,y,z)\in\mathbb{R}^3$$ del siguiente sistema de ecuaciones: $TEX: <br />$\begin{array}{ccccccc}<br />x & + & y^2 & + & z^2 & = & a \\<br />x^2 & + & y & + & z^2 & = & a \\<br />x^2 & + & y^2 & + & z & = & a<br />\end{array}$<br />$ $TEX: <br />escribamos el sistema de la forma<br /><br />$\begin{array}{ccccccc}<br /> 1)& y^2 & + & z^2 & +x & = & a \\<br />2) x^2 & + & z^2 & +& y & = & a \\<br />3) x^2 & + & y^2 & + & z & = & a<br />\end{array}$<br /><br /><br /><br /><br /><br />restemos la primera ecuacion de la segunda y al mismo tiempo la segunda de la tercera<br /><br /><br /> <br />4) $y^{2}-x^{2}+x-y=\allowbreak \left( y-1+x\right) \left( y-x\right) =0$<br /> <br />5) $y^{2}-z^{2}+z-y=\allowbreak \left( y-1+z\right) \left( y-z\right) =0$<br /> <br /><br /> <br />jugando con las ecuaciones tenemos<br /> <br /><br /> <br />$y-x=0,x=y$<br /> <br />$y=z=0,y=z$<br /> <br /><br /> <br />reemplazando estos valores en la ecuacion 1) queda<br /> <br />$x+x^{2}+x^{2}=a,2x^{2}+x-a=0$<br /> <br /><br /> <br />resolviendo y remplazando se obtiene<br /> <br />$2x^{2}+x-a=0$, <br /> <br /><br /> <br />$x_{1}=y_{1}=z_{1}=\dfrac{-1+\sqrt{\left( 1+8a\right) }}{4}$<br /> <br /><br /> <br />$x_{2}=y_{2}=z_{2}=\dfrac{-1-\sqrt{\left( 1+8a\right) }}{4}$<br /> <br /><br /> <br />\bigskip $con$ $1+8a\geq 0,$para raices en los reales<br /> <br />\bigskip jugando otra vez<br /> <br />$y-z=0,y-1+x=0$<br /><br />\bigskip <br /> <br />de aqui<br /> <br />\bigskip $y=z,x=1-y$<br /> <br />reemplazando en 1)<br /> <br />\bigskip $1-y+y^{2}+y^{2}=a$<br /> <br />\bigskip $2y^{2}-y+1-a=0,desarrollando$<br /> <br />$2y^{2}-y+1-a=0$, <br /> <br />\bigskip <br /> <br />$y_{3}=z_{3}=\dfrac{1+\sqrt{\left( 8a-7\right) }}{4}\allowbreak $, $x_{3}=1-y=\dfrac{3-\sqrt{\left( 8a-7\right) }}{4}$<br /> <br />\bigskip <br /> <br />$y_{4}=z_{4}=\dfrac{1-\sqrt{\left( 8a-7\right) }}{4}\allowbreak $, $x_{4}=1-y=\dfrac{3+\sqrt{\left( 8a-7\right) }}{4}$<br /> <br />\bigskip <br /> <br />$con$ $8a-7\geq 0,$para raices en los reales<br /> <br />$ $TEX: <br /> <br />aqui hay varias combinaciones mas , creo que las otras dan numeros no reales<br /> <br />pero tengo mucho tuto , hasta aqui llego....<br /> <br />$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 11 2006, 07:42 AM Publicado: #5
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Este intento se acerca más a la solución del problema. Solamente comento que la separación de casos podría ser bastante agotadora... y recuerda que $TEX: $a$$ es "quien manda". Para cada valor de $TEX: $a$$ tienes que determinar todas las posibles soluciones (o en realidad, el número de ellas). No olvides que en ciertos casos, hay un cierto valor de $TEX: $a$$ que hace coincidir algunas raíces. Cuando lleguemos a una solución correcta, supongo que podré compartir la mía, en caso que sea diferente. Me parece que vas por buen camino, aunque debes tener cuidado con ciertos detalles, y también tengo el temor que la solución resulte muy larga (a mayor extensión, más se agota quien desee revisarla, y más lata da leerla en cualquier caso) Salu -------------------- Sebastián Elías Puelma Moya Administrador FMAT

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 15 2006, 08:56 AM Publicado: #6
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	HINT (Antes que les salgan canas verdes): Vean los casos en que todas las incógnias son iguales, en que dos son iguales y una es distinta, y en que todas son distintas... tengan cuidado al hacer esta separación de casos y después festejamos -------------------- Sebastián Elías Puelma Moya Administrador FMAT

picosenotheta Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 19 2006, 02:54 AM Publicado: #7
Dios Matemático Supremo Grupo: Moderador Mensajes: 765 Registrado: 25-November 05 Desde: Algun lugar de la V region Miembro Nº: 415 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(xsebastian @ Feb 15 2006, 06:56 AM) HINT (Antes que les salgan canas verdes): Vean los casos en que todas las incógnias son iguales, en que dos son iguales y una es distinta, y en que todas son distintas... tengan cuidado al hacer esta separación de casos y después festejamos jugando bastante no llego a más de 8 trios de sol. ¿estoy bien?

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 19 2006, 08:56 AM Publicado: #8
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Supongo que te entendí bien, a ver si puedo responderte De hecho, hay valores de $TEX: $a$$ para los cuales hay ocho soluciones, pero no hay valores de $TEX: $a$$ para los cuales tengamos nueve o más soluciones (recordamos que las soluciones son tríos de números reales, representados por $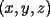TEX: $(x,y,z)$$ ). Ahora, como dice el título, a armarse de paciencia y seguir la indicación que di antes Salu -------------------- Sebastián Elías Puelma Moya Administrador FMAT

pprimo Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 21 2017, 06:26 PM Publicado: #9
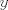Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 817 Registrado: 21-February 14 Miembro Nº: 127.064	Plantearé mi solución aunque no creo que sea así, ya que no pide resolver el sistema, sino que ver el número de soluciones viendo el valor del parámetro $TEX: $\alpha$$ para los números $TEX: $x$$ , $TEX: $y$$ , $TEX: $z$$ reales Tenemos el sistema 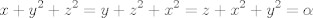$TEX: $$x+y^{2}+z^{2}=y+z^{2}+x^{2}=z+x^{2}+y^{2}=\alpha$$$ Sumemos miembro a miembro las tres ecuaciones 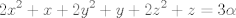$TEX: $$2x^{2}+x+2y^{2}+y+2z^{2}+z=3\alpha$$$ armando cuadrados se puede notar que 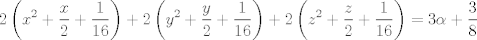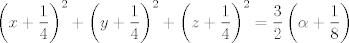$TEX: $$2\left( x^{2}+\frac{x}{2}+\frac{1}{16} \right)+2\left( y^{2}+\frac{y}{2}+\frac{1}{16} \right)+2\left( z^{2}+\frac{z}{2}+\frac{1}{16} \right)=3\alpha +\frac{3}{8}$$$ $TEX: $$\left( x+\frac{1}{4} \right)^{2}+\left( y+\frac{1}{4} \right)^{2}+\left( z+\frac{1}{4} \right)^{2}=\frac{3}{2}\left( \alpha +\frac{1}{8} \right)$$$ Si $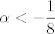TEX: $$\alpha <-\frac{1}{8}$$$ no existe solución para ningún $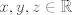TEX: $$x,y,z\in \mathbb{R}$$$ ya que el lado izquierdo de la ecuación sera siempre no negativo $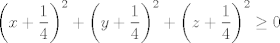TEX: $$\left( x+\frac{1}{4} \right)^{2}+\left( y+\frac{1}{4} \right)^{2}+\left( z+\frac{1}{4} \right)^{2}\ge 0$$$ y el lado derecho de la ecuación será siempre negativo, absurdo. Si $TEX: $$\alpha =-\frac{1}{8}$$$ tenemos $TE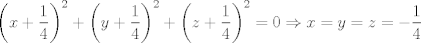X: $$\left( x+\frac{1}{4} \right)^{2}+\left( y+\frac{1}{4} \right)^{2}+\left( z+\frac{1}{4} \right)^{2}=0\Rightarrow x=y=z=-\frac{1}{4}$$$ Si 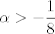$TEX: $$\alpha >-\frac{1}{8}$$$ Hagamos distinción en tres casos: 1. 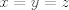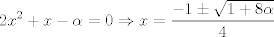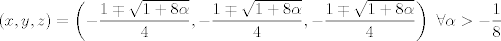Si $TEX: $$x=y=z$$$ es evidente que $TEX: $$2x^{2}+x-\alpha =0\Rightarrow x=\frac{-1\pm \sqrt{1+8\alpha }}{4}$$$ Entonces las soluciones son $TEX: $$\left( x,y,z \right)=\left( -\frac{1\mp \sqrt{1+8\alpha }}{4},-\frac{1\mp \sqrt{1+8\alpha }}{4},-\frac{1\mp \sqrt{1+8\alpha }}{4} \right)\ \forall \alpha >-\frac{1}{8}$$$ 2. 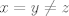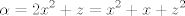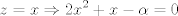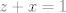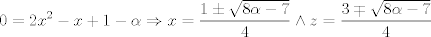Si $TEX: $$x=y\ne z$$$ (o cualquiera de sus permutaciones) tenemos el sistema $TEX: $$\alpha =2x^{2}+z=x^{2}+x+z^{2}$$$ , restando miembro a miembro $TEX: $$0=z^{2}-x^{2}-z+x=\left( z-x \right)\left( z+x-1 \right)$$$ Caso 2.1 $TEX: $$z=x\Rightarrow 2x^{2}+x-\alpha =0$$$ la solución nos lleva al caso anterior Caso 2.2 $TEX: $$z+x=1$$$ implica que $TEX: $$0=2x^{2}-x+1-\alpha \Rightarrow x=\frac{1\pm \sqrt{8\alpha -7}}{4}\wedge z=\frac{3\mp \sqrt{8\alpha -7}}{4}$$$ Entonces 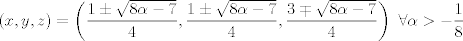$TEX: $$\left( x,y,z \right)=\left( \frac{1\pm \sqrt{8\alpha -7}}{4},\frac{1\pm \sqrt{8\alpha -7}}{4},\frac{3\mp \sqrt{8\alpha -7}}{4} \right)\ \forall \alpha >-\frac{1}{8}$$$ Por último, si 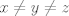$TEX: $$x\ne y\ne z$$$ podemos notar que no hay solución, puesto que si restamos las primeras dos ecuaciones miembro a miembro $TEX: $$0=x-y+y^{2}-x^{2}=\left( \underbrace{x-y}_{x\ne y} \right)\left( 1-\left( x+y \right) \right)\Rightarrow y=1-x$$$ reemplazando $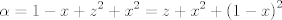TEX: $$\alpha =1-x+z^{2}+x^{2}=z+x^{2}+\left( 1-x \right)^{2}$$$ factorizando 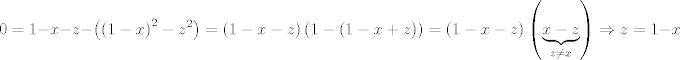$TEX: $$0=1-x-z-\left( \left( 1-x \right)^{2}-z^{2} \right)=\left( 1-x-z \right)\left( 1-\left( 1-x+z \right) \right)=\left( 1-x-z \right)\left( \underbrace{x-z}_{z\ne x} \right)\Rightarrow z=1-x$$$ llegamos a 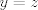$TEX: $$y=z$$$ contradicción ya que supusimos que $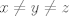TEX: $$x\ne y\ne z$$$ , se pudo haber hecho de manera similar para las otras variables. 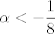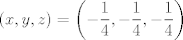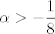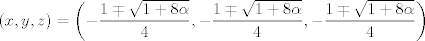Resumen, Si $TEX: $$\alpha <-\frac{1}{8}$$$ No hay soluciones reales Si $TEX: $$\alpha =-\frac{1}{8}$$$ Tenemos la solución al sistema $TEX: $$\left( x,y,z \right)=\left( -\frac{1}{4},-\frac{1}{4},-\frac{1}{4} \right)$$$ Si $TEX: $$\alpha >-\frac{1}{8}$$$ Tenemos las soluciones al sistema $TEX: $$\left( x,y,z \right)=\left( -\frac{1\mp \sqrt{1+8\alpha }}{4},-\frac{1\mp \sqrt{1+8\alpha }}{4},-\frac{1\mp \sqrt{1+8\alpha }}{4} \right)$$$ $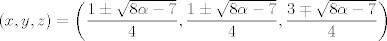TEX: $$\left( x,y,z \right)=\left( \frac{1\pm \sqrt{8\alpha -7}}{4},\frac{1\pm \sqrt{8\alpha -7}}{4},\frac{3\mp \sqrt{8\alpha -7}}{4} \right)$$$ y sus permutaciones, por lo tanto en total son 9 soluciones del sistema Saludos.

Legition Rompedi... Legition Rompediskoteqa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 21 2017, 07:17 PM Publicado: #10
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.566 Registrado: 20-June 11 Desde: Region del Maule Miembro Nº: 90.738 Sexo:	llegue a lo mismo que pprimo, las mismas contradicciones, elevando al cuadrado x,y,z sumando 0, despues iguale los a, llego a que necesariamente x=y=z. Mensaje modificado por Legition Rompediskoteqa el Jul 22 2017, 09:06 AM -------------------- Actualmente en Ingenieria Industrial y en 3er año Ingeniería Civil Mecánica. From my personal life: I highly recommend this video Click Here! Es altamente deseable tener aptitud para la quimica(termodinámica), la programación, alta comprensión de un problema y planteamiento del mismo, y tener resiliencia al estudiar Ingenieria Civil Industrial. Civil Industrial es en gran parte saber levantar(modelar problemas) procesos logísticos. Puedo dar fe que la Universidad Nacional Andres Bello está adelante de varias U'es Regionales(Calidad similar a la UTAL). Realidad universidades del mundo (18:30): Youtube Quiten Filosofia, Musica y Religión del Curriculum de la Media!! No es recomendado trabajar/colaborar entre matemáticos en general. En general, y a menos que Chile gaste mínimo 2% PIB en I+D, quedarse a investigar en el país, es matarse académicamente. Como recomendación Brasil es un pais muy adelantado en investigación versus AL. Gasto 2023: 0,34%.

« Posterior · Problemas Propuestos · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 02:49 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.