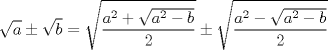Fórmulas - Foro fmat.cl

8 Páginas:

« < 3 4 5 6 7 > »

Fórmulas

Opciones

TheAvenger Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 19 2008, 11:50 PM Publicado: #41
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 590 Registrado: 5-January 08 Desde: Valdivia. Miembro Nº: 14.345 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Initium @ Jun 21 2008, 04:51 PM) para trigonometria el las razones trigonometricas el co ca co ca hip hip tienen que aprenderse este orden. sen - cos - tang - cotang - sec - cosec entonces empiezan a poner "co - ca - co - ca - hip - hip" en todos los numeradores de las razones....asi: y despues denuevo escriben "co - ca - co - ca - hip - hip" pero desde abajo y en el denominador...asi: y ahi estan todas sus razones trigonometricas... Notable, si se fijan es cómo decir Coca Cola Hip Hip!.. muy rebueno. sl2! -------------------- Medicina - 4º Año Twitter Facebook

hsigrist Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 23 2008, 12:44 PM Publicado: #42
Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 26-January 08 Miembro Nº: 15.000 Nacionalidad: Universidad: Sexo:	Para razones trigonométricas de los ángulos fundamentales (para ángulos intermedios o factores usar seno y/o coseno del ángulo medio y/o doble). Buscar ángulo en la fila de arriba y hacerlo coincidir con la función trigonométrica buscada, calcular la raíz y luego dividir por dos. Razones_trig.tiff ( 23.65k ) Número de descargas: 136

Kapranos Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 23 2008, 04:08 PM Publicado: #43
Matemático Grupo: Usuario FMAT Mensajes: 60 Registrado: 18-June 08 Desde: Maipu Miembro Nº: 27.542 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(TheAvenger @ Jul 19 2008, 11:40 PM) Notable, si se fijan es cómo decir Coca Cola Hip Hip!.. muy rebueno. sl2! ese es muy bueno, al igual que el de la raiz para obtener los valores de la funciones mas comunes, 30 45 60 90 --------------------

Soul_Hunter Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2008, 05:31 PM Publicado: #44
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	bisectriz.PNG ( 13.11k ) Número de descargas: 6 $TEX: \noindent Dado un $\triangle ABC$, la longitud de la bisectriz de un ángulo $\gamma$ es $$w_{\gamma}=\dfrac{2ab}{a+b}\left( \cos \dfrac{\gamma}{2}\right)$$ Si se quiere evitar el uso de la trigonometría, también puede usarse la fórmula $$w_{\gamma}=\sqrt{ab\left( 1-\dfrac{c^2}{(a+b)^2}\right)}$$$ --------------------

Soul_Hunter Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 2 2008, 05:44 PM Publicado: #45
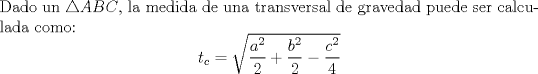
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	transversal.PNG ( 13.56k ) Número de descargas: 7 $TEX: \noindent Dado un $\triangle ABC$, la medida de una transversal de gravedad puede ser calculada como: $$t_c=\sqrt{\dfrac{a^2}{2}+\dfrac{b^2}{2}-\dfrac{c^2}{4}}$$$ Mensaje modificado por Apolonio el Sep 27 2008, 10:13 PM --------------------

benjamin demarco Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 4 2008, 10:03 PM Publicado: #46
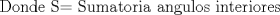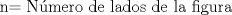
Maestro Matemático Grupo: Usuario FMAT Mensajes: 88 Registrado: 9-July 08 Desde: Viña del mar Miembro Nº: 29.553 Nacionalidad: Universidad: Sexo:	$TEX: Sumatoria de angulos interiores:$ $TEX: S= 180º (n-2)$ $TEX: Donde S= Sumatoria angulos interiores$ $TEX: n= Número de lados de la figura$ -------------------- El 98% de los adolescentes han fumado, si eres del dichoso 2% que no lo ha hecho, copia y pega esto en tu firma

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 19 2008, 05:13 PM Publicado: #47
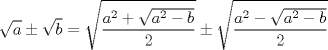Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: Radicales dobles$ $TEX: $$<br />\sqrt a \pm \sqrt b = \sqrt {\frac{{a^2 + \sqrt {a^2 - b} }}<br />{2}} \pm \sqrt {\frac{{a^2 - \sqrt {a^2 - b} }}<br />{2}} <br />$$$

Soul_Hunter Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 19 2008, 08:09 PM Publicado: #48
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 665 Registrado: 12-June 07 Desde: the city of the fallen angels Miembro Nº: 6.649 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(vivanco @ Aug 19 2008, 05:04 PM) $TEX: Radicales dobles$ $TEX: $$<br />\sqrt a \pm \sqrt b = \sqrt {\frac{{a^2 + \sqrt {a^2 - b} }}<br />{2}} \pm \sqrt {\frac{{a^2 - \sqrt {a^2 - b} }}<br />{2}} <br />$$$ Ya estaba... --------------------

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 20 2008, 09:50 PM Publicado: #49
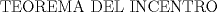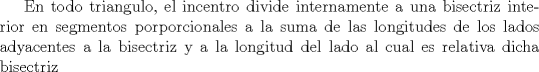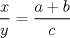Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: TEOREMA DEL INCENTRO$ $TEX: En todo triangulo, el incentro divide internamente a una bisectriz interior en segmentos porporcionales a la suma de las longitudes de los lados adyacentes a la bisectriz y a la longitud del lado al cual es relativa dicha bisectriz$ $TEX: $$<br />\frac{x}<br />{y} = \frac{{a + b}}<br />{c}<br />$$$

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	Aug 20 2008, 09:52 PM Publicado: #50
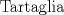Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: Tartaglia$ $TEX: formula para hallar el volumen de un tetraedro$ $TEX: $$<br />v = a^3 \frac{1}<br />{{12}}\sqrt 2 <br />$$$

8 Páginas:

« < 3 4 5 6 7 > »

3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 3rd April 2025 - 05:44 AM