EDP #9 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Ecuaciones Diferenciales > EDP

Reply to this topic

Start new topic

EDP #9

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 5 2007, 10:47 PM Publicado: #1
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	$TEX: \noindent Resolver el problema de Dirichlet sobre un anillo, si $\Delta u=0$ en toda la region, $u(1,\theta)=1$ y, $u(2, \theta)=sin^2(\theta)$<br /><br />( Debe determinar $u(r, \theta)$ en las tres regiones diferentes que se forman)$ salu2

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 2 2010, 01:27 AM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	¿Alguien me podría decir exactamente cual es la "región"?¿Es todo el disco de radio 2? -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

aleph_omega Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 2 2010, 12:59 PM Publicado: #3
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 560 Registrado: 24-December 09 Miembro Nº: 64.629	En el problema se dice que la región de referencia es un anillo. Por lo datos del problema se infiere que la región de referencia es 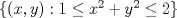$TEX: $\{(x,y):1\leq x^2+y^2\leq 2\}$$ las "tres regiones que se forman" serían adentro del anillo , el circulo de radio 1 que esta al exterior del anillo ( "region encerrada por el anillo"), y lo que está afuera (mas alla de radio 2). Luego " La Región Total" es todo el plano. Mensaje modificado por aleph_omega el Jul 2 2010, 01:03 PM

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 2 2010, 01:42 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(aleph_omega @ Jul 2 2010, 01:59 PM) En el problema se dice que la región de referencia es un anillo. Por lo datos del problema se infiere que la región de referencia es 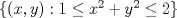$TEX: $\{(x,y):1\leq x^2+y^2\leq 2\}$$ las "tres regiones que se forman" serían adentro del anillo , el circulo de radio 1 que esta al exterior del anillo ( "region encerrada por el anillo"), y lo que está afuera (mas alla de radio 2). Luego " La Región Total" es todo el plano. Aaa dale -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 13 2010, 10:48 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Estuve tratando de hacer el problema, pero me pasó algo curioso: $TEX: \noindent Buscamos una solución de la forma <br />\begin{equation}u(r,\theta)=f®g(\theta).\end{equation}<br />Así, se tiene que<br />\[g\left(f''+\frac 1rf'\right)+\frac1{r^2}fg''=0,\]<br />es decir,<br />\begin{equation}\frac{r^2}f\left(f''+\frac 1rf'\right)=-\frac{g''}{g}.\end{equation}<br />Sea $\lambda^2$ la constante de separación, entonces resolvemos<br />\begin{equation}g''+\lambda^2 g=0.\end{equation}<br />Luego, $g=e^{\pm i\theta}$. Como además, debe tenerse que $u(r,\theta)=u(r,\theta+2\pi)$, entonces $\lambda=n\in\mathbb{N}_0$. Así, nos queda<br />\begin{equation}f''+\frac 1rf'-\frac{n^2}{r^2}f=0.\end{equation}<br />Dada su homogeneidad, planteamos una solución de la forma $f=Cr^\beta$ y reemplazando, se obtiene que $\beta=\pm n$. Como queremos que el mundo no explote en $r=0$, nos quedamos con $\beta>0$.\\<br />\\<br />En consecuencia, dado que suma de soluciones de Laplace es solución, planteamos una solución de la forma<br />\begin{equation}u(r,\theta)=\sum_{n=0}^\infty r^n\left(a_ne^{in\theta}+b_ne^{-in\theta}\right).\end{equation}<br />Si impongo<br />\[\sum_{n=0}^\infty \left(a_ne^{in\theta}+b_ne^{-in\theta}\right)=1,<br />\]<br />para $n>0$<br />\[a_n=\frac{1}{2\pi}\int_{0}^{2\pi}e^{-in\theta}d\theta=0 \quad , \quad <br />b_n=\frac{1}{2\pi}\int_{0}^{2\pi}e^{in\theta}d\theta=0,\]<br />y<br />\[a_0+b_0=1\Rightarrow u\equiv 1.\]$ Que es lo que uno esperaría pues $TEX: $u$$ es armónica. Sin embargo, si impongo la otra condición, tengo que $TEX: \noindent Para $n\ne 2,n>0$, <br />\[a_n=\frac{1}{2^n 2\pi}\int_{0}^{2\pi}\sin^2\theta e^{-in\theta}d\theta=0 \quad , \quad <br />a_n=\frac{1}{2^n 2\pi}\int_{0}^{2\pi}\sin^2\theta e^{in\theta}d\theta=0,\]<br />y<br />\[a_0+b_0=\frac{1}{2}\quad , \quad a_2=b_2=-\frac{1}{8}.\]<br />Es decir, obtengo <br />\[u(r,\theta)=\frac{1}{2}-\frac{r^2}{8}\cos 2\theta.\]<br />$ --- Por lo cual pensaría que este tipo de problemas no se pueden resolver así o no D:? -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

« Posterior · EDP · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:55 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.