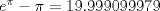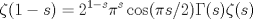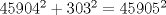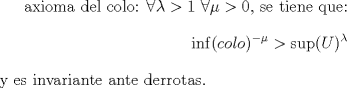|
|
|
|
|
|
|
  |
 Jan 1 2006, 11:57 PM Jan 1 2006, 11:57 PM
Publicado:
#1
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Antes de iniciar este Capitulo debo confesar que esta es una de las Desigualdades que mas me gusta...y a la cual le he dado mucha utilidad en variadas Olimpiadas.
Por fin aprenderemos algo realmente lindo....jejejejejeje(y de paso nos toparemos con calculo) Consideremos 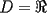 o bien o bien 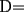 Intervalo en Intervalo en 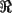 (en el futuro diremos que D es un conjunto convexo) (en el futuro diremos que D es un conjunto convexo)Una funcion 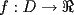 se dira Convexa si: se dira Convexa si:![TEX: $\left(\forall x,y\in D\right)\left(\forall \lambda\in[0,1]\right) f((1-\lambda)x+\lambda y)\le (1-\lambda) f(x)+\lambda f(y)$](./tex/8087.gif) Graficamente esto significa que en cada intervalo ![TEX: [x,y]](./tex/8093.gif) , la grafica de , la grafica de 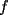 queda por debajo del segmento que une queda por debajo del segmento que une 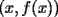 con con 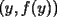 Esto lo podemos visualizar en el siguiente "Grafico Ilustrativo"  screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img313.imageshack.us/img313/9934/convexa2zm.png');}" /> screen.width*0.6) {this.resized=true; this.width=screen.width*0.4; this.alt='Pincha Aqui para ver esta imagen en su tamaño original';}" onmouseover="if(this.resized) this.style.cursor='hand';" onclick="if(this.resized) {window.open('http://img313.imageshack.us/img313/9934/convexa2zm.png');}" />De la misma forma 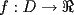 se dira Concava si: se dira Concava si:![TEX: $\left(\forall x,y\in D\right)\left(\forall \lambda\in[0,1]\right) f((1-\lambda)x+\lambda y)\ge (1-\lambda) f(x)+\lambda f(y)$](./tex/8088.gif)
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 12:48 AM Jan 2 2006, 12:48 AM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Algunos ejemplos de Funciones Convexas importantes:
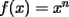 con con 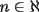 y y 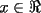 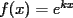 con con 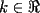 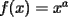 con con 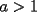 y y 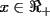 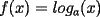 con con 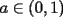 y y 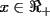 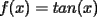 para para 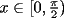 Algunos ejemplos de Funciones Concavas importantes: 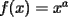 para para 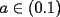 y y 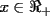 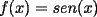 para para ![TEX: $x\in[0,\pi]$](./tex/8147.gif) (Una de mis favoritas,y que no se malentienda (Una de mis favoritas,y que no se malentienda 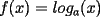 para para 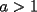 y y 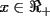 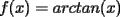 para para 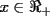
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 01:11 AM Jan 2 2006, 01:11 AM
Publicado:
#3
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Para aquellos que se manejen un poco en Calculo Diferencial, si
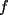 resulta ser derivable entonces sera convexa si resulta ser derivable entonces sera convexa si 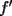 es creciente en es creciente en 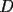 . .Si 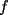 es dos veces derivable basta verificar que es dos veces derivable basta verificar que 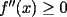 para para 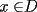 Nota:Esto no quiere decir que todas las funciones convexas(o concavas) tienen que ser derivables...solo indico que si lo fueran,seria "mas facil"(dependiendo el caso) saber si son o no convexas(o concavas). Como ultimo comentario,se tiene la siguiente equivalencia: 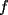 es concava es concava  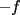 es convexa es convexa(esto ultimo independiente de que 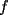 sea o no sea derivable) sea o no sea derivable)Finalmente el Gran Momento ![TEX: \[ \boxed{Desigualdad\ de\ Jensen}\]](./tex/8187.gif) Sea 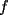 una funcion convexa en una funcion convexa en 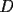 , , 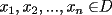 y y 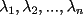 reales positivos reales positivostales que: 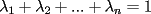 Bajo estas condiciones se cumple que: 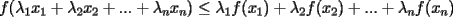 Demostracion: Nuestra demostracion la haremos por Induccion sobre  ![TEX: \[\boxed{Si\ n=2}\]](./tex/8192.gif) Eso es simplemente la desigualdad de la Convexidad, y por ende se cumple( Eso es simplemente la desigualdad de la Convexidad, y por ende se cumple(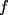 es convexa) es convexa)![TEX: \[\boxed{H.I.}\]](./tex/8223.gif) Supongamos que para cierto Supongamos que para cierto  es cierta la propiedad, o sea que: es cierta la propiedad, o sea que:Si 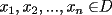 y y 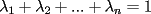 ( (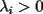 ) entonces: ) entonces: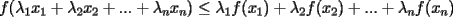 ![TEX: \[\boxed{P.d.q.}\]](./tex/8226.gif) La propiedad es valida tambien para La propiedad es valida tambien para 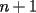 Esto es: Si 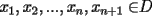 y y 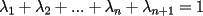 ( (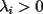 ) entonces: ) entonces: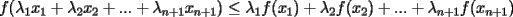 Ahora viene la parte interesante,o sea la demostracion en si: Caso 1 Si 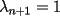 entonces entonces 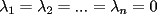 y la desigualdad se transforma en una igualdad. y la desigualdad se transforma en una igualdad.Caso 2 Entonces veamos que sucede si 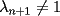 Definamos 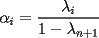 para para 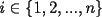 Notemos que 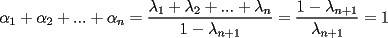 Notemos que: 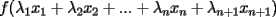 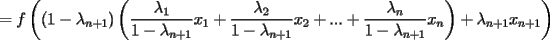 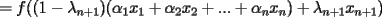 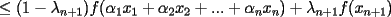 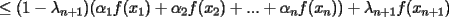 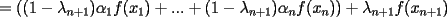 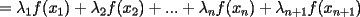 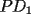 : El primer : El primer  fue porque fue porque 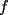 es convexa es convexaEsto tomando: 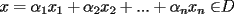 pues pues 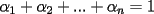 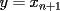 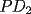 : El segundo : El segundo  por la por la 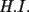 y porque y porque 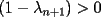 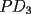 : En el caso que la funcion : En el caso que la funcion 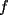 fuese concava la demostracion es identica,y el teorema solo cambia en el sentido de la desigualdad(cambia de fuese concava la demostracion es identica,y el teorema solo cambia en el sentido de la desigualdad(cambia de 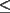 a a  ) )
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 02:43 AM Jan 2 2006, 02:43 AM
Publicado:
#4
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 1:
Probar que 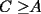 (esto ya lo probamos antes usando Cauchy-Shwarz-Bunyakowsky) (esto ya lo probamos antes usando Cauchy-Shwarz-Bunyakowsky)Solucion: Consideremos 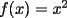 una funcion convexa, una funcion convexa,y 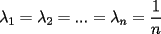 Luego aplicando la Desigualdad de Jensen tendremos que: 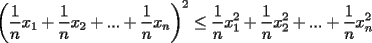 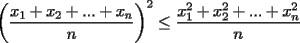 Considerando el hecho que 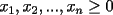 , al aplicar raiz cuadrada a ambos lados tendremos: , al aplicar raiz cuadrada a ambos lados tendremos: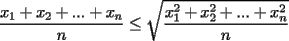
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 02:54 AM Jan 2 2006, 02:54 AM
Publicado:
#5
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 2:
Probar que  (demostrado anteriormente en el Capitulo II) (demostrado anteriormente en el Capitulo II)Solucion: Consideremos 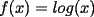 (una funcion concava para (una funcion concava para 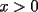 ) ) y 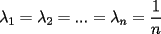 Consideremos tambien 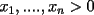 Entonces: 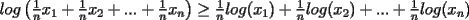 O sea: ![TEX: $\displaystyle log\left(\frac{x_1+x_2+...+x_n}{n}\right)\ge log(\sqrt[n]{x_1x_2...x_n})$](./tex/8286.gif) y considerando el hecho de que 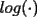 es una funcion estrictamente creciente tendremos que: es una funcion estrictamente creciente tendremos que: ![TEX: $\displaystyle \frac{x_1+x_2+...+x_n}{n}\ge\sqrt[n]{x_1x_2...x_n}$](./tex/8287.gif) El caso en que algun 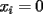 es elemental pues en ese caso es elemental pues en ese caso 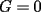 y y 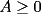
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 03:14 AM Jan 2 2006, 03:14 AM
Publicado:
#6
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 3:
Si 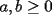 y y 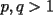 son exponentes conjugados, o sea: son exponentes conjugados, o sea: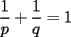 Entonces: 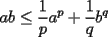 Solucion: Consideremos 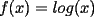 (una funcion concava para (una funcion concava para 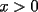 ) ) 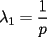 , , 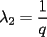 (notar que (notar que 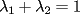 por enunciado) por enunciado)y 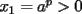 y y 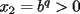 Los casos 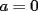 o o 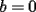 son directos. son directos.Aplicando la Desigualdad de Jensen tendremos: 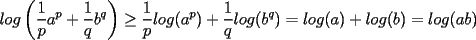 Considerando el hecho de que 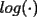 es una funcion estrictamente creciente tendremos que: es una funcion estrictamente creciente tendremos que: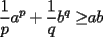
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jan 2 2006, 03:35 AM Jan 2 2006, 03:35 AM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Ejemplo 4:
Se define las Medias "Pesadas" de la siguiente manera: Sean 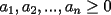 reales tales que: reales tales que: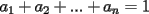 y sean 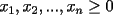 y no nulos si es necesario. y no nulos si es necesario.Se define la Media Aritmetica Pesada como: 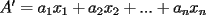 Se define la Media Geometrica Pesada como: 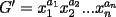 Se define la Media Armonica Pesada como: 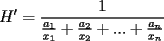 Notemos que 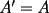 si si 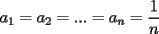 Asi tambien ocurre con 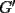 y y 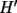 Probar que 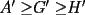 Solucion: Primer Paso: Probemos que 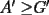 Si algun 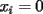 la desigualdad es inmediata. Supongamos entonces que la desigualdad es inmediata. Supongamos entonces que 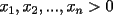 Si consideramos 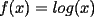 (funcion concava para (funcion concava para 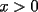 ) )y 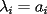 para para 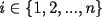 (notar que (notar que 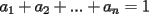 Luego aplicando la Desigualdad de Jensen tendremos: 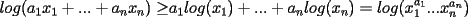 Considerando el hecho de que 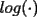 es una funcion estrictamente creciente tendremos que: es una funcion estrictamente creciente tendremos que: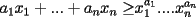 Segundo Paso: Basta aplicar la desigualdad 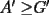 recien demostrada a los reales positivos recien demostrada a los reales positivos 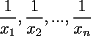 considerando que considerando que 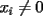 para todo para todo 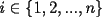
-------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Jul 8 2013, 06:13 PM Jul 8 2013, 06:13 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.879 Registrado: 27-December 07 Desde: ∂Ω©ȹʕѺϧگἐᾋ1©Ӹ█₯►☻X TH.....I FORGOR Miembro Nº: 14.122 Nacionalidad:  Universidad:  Sexo:  |
Una cosa: personalmente prefiero el termino "ponderadas" que "pesadas"... es que me suena como la cancion esa de los tres: somos tontos, no pesados...
Consecuencias interesantes: 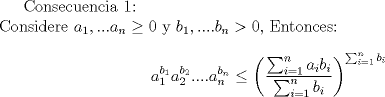 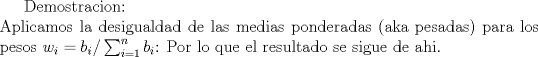    Saludos. Claudio. PD: alguna falencia, avise no mas. -------------------- Claudio Henriquez Tapia Ingeniero Civil Matemático UTFSM y Prof. DMAT UTFSM Candidato a Doctor en Estadística UC. Campus San Joaquin Si todo sale bien, estaría defendiendo en Julio 2024. [indent] everywhere at the end of FMAT fmat needs .... To Survive... 3ch03s facts: Frases para el bronce by 3ch03s: Fmat dejame subir mas citas! TB-3030303 que es YTP-Tennis: |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 8th July 2025 - 01:57 AM |