multi-índices - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Desafíos > Problemas Resueltos

2 Páginas:

1 2 >

Reply to this topic

Start new topic

multi-índices, Multinomio de Newton y otros

Cesarator	Dec 28 2005, 04:00 PM Publicado: #1
Invitado	$TEX: Un {\bf $k$-Multiindice} es una $k-$upla de la forma<br />$$<br />N = (n_1, \dots, n_k),<br />$$<br />donde cada $n_i$ es un entero no negativo. Dado un vector $x=(x_1, \dots, x_k) \in \mathcal{R}^k$, se define<br />$$<br />x^N = x_1^{n_1}x_2^{n_2}\cdots x_k^{n_k}.<br />$$<br />Tambi\'en se definen<br />$$<br />\|N\| = n_1 + ... +n_k, \ N! = n_1! \dots n_k!.<br />$$<br /><br />{\bf Ejercicio}. Demostrar el teorema multinomial:<br />$$<br />(x_1 + ... + x_k)^n = \sum_{\|N\|=n}{n \choose N} x^N,<br />$$<br />donde $x = (x_1, ..., x_k)$ y ${n \choose N} = n!/ N!$.<br /><br />>Es coherente esta f\'ormula con la del binomio de Newton, v\'alida para $k=2$?<br />$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 1 2006, 12:30 PM Publicado: #2
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Con las notaciones definidas para el problema, hacemos el proceso de multiplicar todos contra todos y agrupar términos semejantes, para obtener: 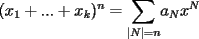$TEX: $\displaystyle{(x_1+...+x_k)^n=\sum_{\|N\|=n}}a_Nx^N$$ , y apenas debemos demostrar que 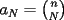$TEX: $a_N={n \choose N}$$ . 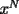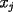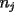Pero esto último es bastante sencillo de la combinatoria, porque la cantidad de factores $TEX: $x^N$$ es igual a la cantidad de filas de largo n, si el total de términos $TEX: $x_j$$ es igual a $TEX: $n_j$$ Más adelante explicaré con más detalles, si fuese necesario. -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Jorge_Littin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 24 2006, 09:33 PM Publicado: #3
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 20-February 06 Miembro Nº: 579	El binomio de Newton es un caso particular de ésta formula multinomial, y por lo tanto la incluye

Cesarator	Feb 25 2006, 12:02 PM Publicado: #4
Invitado	... no entiendo lo que quieres decir... o peor, si lo entiendo y es absolutamente errado. Bienvenido a fmat !!

Jorge_Littin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 25 2006, 10:18 PM Publicado: #5
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 20-February 06 Miembro Nº: 579	Dime cualquier cosa, menos que lo que digo está errado. Busca en cualquier libro de matemática la fórmula multinomial, y dirá que el binomio de Newton es un caso particular de ésta generalización.

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 25 2006, 11:14 PM Publicado: #6
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(Jorge_Littin @ Feb 26 2006, 12:18 AM) Dime cualquier cosa, menos que lo que digo está errado. Busca en cualquier libro de matemática la fórmula multinomial, y dirá que el binomio de Newton es un caso particular de ésta generalización. Veamos...primera cosa...no te enojes...si solo te dijeron que no te comprendian lo que decias...nada mas..o que "quizas" estaba errado, al menos en la forma en que lo estabas expresando. No estaria de mas que supieras que Cesarator es Docente de la Universidad de Concepcion y el seguramente te dijo eso por algo. Aunque este correcto lo que tu dices(yo al menos creo haber entendido lo que dices, y en realidad es algo bastante evidente) no puedes molestarte porque alguien pone en duda una respuesta, pues nadie aca lo hace en "mala" ni mucho menos, todos aca estamos voluntariamente y compartimos nuestros conocimientos y experiencias...asi que amor y paz... Bienvenido y bueno, esperemos a ver cual es el motivo por el cual Cesarator dijo lo que dijo(mi intuicion me dice que quizas el creyo que tu decias que con Newton podrias obtener la formula Multinomial) Saludos PD:La idea es conversar..siempre en buena, y no tomarse a mal los comentarios... -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

Jorge_Littin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 25 2006, 11:31 PM Publicado: #7
Principiante Matemático Grupo: Usuario FMAT Mensajes: 11 Registrado: 20-February 06 Miembro Nº: 579	Ningún problema con moderar el lenguaje. Si la persona que tu mencionas es donde de la UDEC, me alegro, no sabía bien que era de buen nivel el foro. De todos modos, a mí me atrae la idea de participar acá, pues como todos sabemos la familia matemática es reducida.

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 25 2006, 11:34 PM Publicado: #8
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	CITA(Jorge_Littin @ Feb 26 2006, 01:31 AM) Ningún problema con moderar el lenguaje. Si la persona que tu mencionas es donde de la UDEC, me alegro, no sabía bien que era de buen nivel el foro. De todos modos, a mí me atrae la idea de participar acá, pues como todos sabemos la familia matemática es reducida. Si pues, y la idea es poder llevarnos bien entre nosotros Bienvenido a la familia y esperemos seguir creciendo y tener cada dia mas y mejores elementos...asi poder compartir las diferentes visiones.... Esperamos ver futuros aportes Saludos -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 26 2006, 11:07 AM Publicado: #9
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Yo estaba a la espera de un veredicto, por parte de Cesarator, hacia mi solución, que puse al comienzo. Yo no dudo que lo haya hecho bien, pero me preocupa saber qué tan entendible fue mi aporte. Supongo que dar algunos detalles resultará educativo. Veamos: La principal dificultad para establecer este teorema mío (y de todos quienes pudimos resolverlo sin ayuda) está en escribir lo que muchas veces puede intuirse con algunos ejemplos o casos particulares. Uno de los primeros ejemplos no triviales, es mirar lo que sucede al expresar 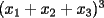$TEX: $(x_1+x_2+x_3)^3$$ . 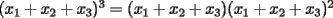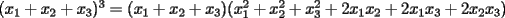Sólo con la experiencia del álgebra de enseñanza media (cubo de binomio y otros similares) podemos hacer lo siguiente $TEX: $(x_1+x_2+x_3)^3=(x_1+x_2+x_3)(x_1+x_2+x_3)^2$$ $TEX: $(x_1+x_2+x_3)^3=(x_1+x_2+x_3)(x_1^2+x_2^2+x_3^2+2x_1x_2+2x_1x_3+2x_2x_3)$$ Antes de desarrollar todo esto, vemos que nos quedará algo con la siguiente forma: 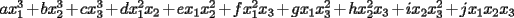$TEX: $ax_1^3+bx_2^3+cx_3^3+dx_1^2x_2+ex_1x_2^2+fx_1^2x_3+gx_1x_3^2+hx_2^2x_3+ix_2x_3^2+jx_1x_2x_3$$ La tarea final es encontrar los coeficientes 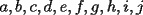$TEX: $a,b,c,d,e,f,g,h,i,j$$ . Se puede hacer en este ejemplo, desarrollando el producto, pero nuestro objetivo es dar con un método más interesante La respuesta en este ejemplo es: 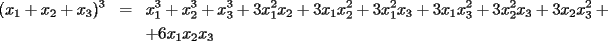$TEX: \begin{eqnarray}<br />(x_1+x_2+x_3)^3 & = & x_1^3+x_2^3+x_3^3+3x_1^2x_2+3x_1x_2^2+3x_1^2x_3+3x_1x_3^2+3x_2^2x_3+3x_2x_3^2+ \\<br /> & & +6x_1x_2x_3<br />\end{eqnarray}$ Viene al caso hacer preguntas como: ¿Por qué el monomio 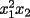$TEX: $x_1^2x_2$$ tiene un coeficiente 3? El problema queda finalmente resuelto al entender este último paso. Y para eso necesitamos saber combinatoria. Volviendo a nuestro ejemplo, tenemos, por distributividad, lo siguiente (con ayuda de la notación de sumatoria, nos posicionamos antes de agrupar términos semejantes): 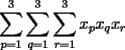$TEX: $\displaystyle{\sum_{p=1}^3\sum_{q=1}^3\sum_{r=1}^3x_px_qx_r}$$ Después de esto, vamos a agrupar términos semejantes, o sea los monomios con los mismos factores pero en orden distinto. 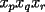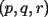Lo que nos conviene, es asociar al monomio $TEX: $x_px_qx_r$$ la terna $TEX: $(p,q,r)$$ . Son 27 ternas diferentes. Cuando agrupamos términos semejantes, estamos confundiendo aquellas ternas que tienen los mismos términos pero en distinto orden. Eso se cuenta con el símbolo multinomial $TEX: $\displaystyle{n \choose N}$$ . 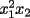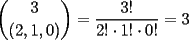Así, en nuestro caso: $TEX: $x_1^2x_2$$ tiene coeficiente $TEX: $\displaystyle{{3 \choose (2,1,0)}=\frac{3!}{2!\cdot 1!\cdot 0!}=3}$$ La explicación de esto último, cuando se desarrolle un capítulo de combinatoria básica, en este foro, para eso se necesita un poco de paciencia. El binomio de Newton es caso particular de este teorema nuestro, haciendo 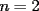$TEX: $n=2$$ Por otra parte, también es posible demostrar nuestro teorema con ayuda del binomio de Newton, pero esa demostración es inductiva y no tan intuitiva como la que acabo de explicar. Por eso no tuve dónde perderme para colocar una demostración y no otra Salu -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Cesarator	Feb 28 2006, 02:37 PM Publicado: #10
Invitado	ok, bastante clara y muy correcta la respuesta de xsebastian. Igual se reduce a la resolución de un problema de combinatoria, lo cual es típico de estas cosas. Con respecto a lo dicho por Jorge_Littin, bueno, a veces uno escribe corto de tiempo y no se explica mucho. Quise decir dos cosas. Primero, es verdad que el binomio de Newton es un caso particular de la fórmula multinomial (lo que es casi trivial de ver y se dice en el enunciado del problema a manera de pregunta). Sin embargo, no es cierto que por ese sólo motivo el Binomio de Newton contenga a la fórmula. Esta es más general que aquél, y necesita demostración.

« Posterior · Problemas Resueltos · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 03:33 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.