APMO 1994 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Competencias y Olimpiadas > Olimpiadas > Olimpiada Asia-Pacifico

Reply to this topic

Start new topic

APMO 1994, Ssp: 1,3,4

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 17 2007, 07:44 PM Publicado: #1
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent \underline{$Problema\ 1$} Sea $f:\mathbb{R}\rightarrow \mathbb{R}$ una funci\'on tal que:\\<br />\\<br />(i) $\forall x,y \in \mathbb{R}$, $f(x)+f(y)+1\ge f(x+y) \ge f(x)+f(y)$\\<br />\\<br />(ii) $\forall x \in [0,1), f(0) \ge f(x)$\\<br />\\<br />(iii) $-f(-1)=f(1)=1$\\<br />\\<br />Encuentre todas las funciones $f$.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 2$} Pruebe que la distancia entre el ortocentro y el circuncentro es menor que tres veces el circunradio en cualquier tri\'angulo $ABC$.$ Solucion: $TEX: <br />Caso 1: $\triangle ABC$ acut\'angulo. Tenemos que recordar que en un tri\'angulo acut\'angulo el ortocentro y el circuncentro son interiores al tri\'angulo, por lo que la distancia entre $O$ y $H$ pertenece dentro de la circunferencia, esto significa que $OH<2R<3R\Rightarrow OH<3R$.\\<br /><br />Caso 2: $\triangle ABC$ rect\'angulo. Tenemos en este caso que el circuncentro es el punto medio de la hipotenusa y el ortocentro es el v\'ertice opuesto a la hipotenusa, por lo que $OH$ en el fondo es la mediana, igual al circunradio del tri\'angulo, que es menor que $3$ veces el mismo xD.\\<br /><br />Caso 3: $\triangle ABC$ obtus\'angulo. Tenemos que recordar que $O,G,H$ son colineales y $2OG=GH$, por lo que $OG=\frac{OH}{3}$. Ahora notemos que $G$ siempre pertenece al interior de todo tri\'angulo, por lo que $G$ est\'a dentro de su circunscrita. Entonces $OG<r\Rightarrow \frac{OH}{3}<r\Rightarrow OH<3r$, con lo que queda probado pa los $3$ casos =D!!!\\$ $TEX: $\boxed{Resuelto\ por\ pelao\ malo}$$ $TEX: \noindent \underline{$Problema\ 3$} Encuentre todos los enteros positivos $n$ tales que $n=a^2+b^2$, donde $a$ y $b$ son enteros positivos coprimos, y para cada primo $p$ con $p\le \sqrt{n}$ se cumple que $p\|ab$.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 4$} Diga si es posible encontrar un conjunto infinito de puntos en el plano tal que no hay tres puntos colineales y la distancia entre dos puntos cualquiera es racional. 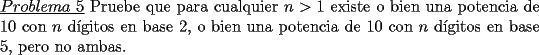Justifique su respuesta.$ Solucion: (Pendiente) $TEX: \noindent \underline{$Problema\ 5$} Pruebe que para cualquier $n>1$ existe o bien una potencia de 10 con $n$ d\'igitos en base 2, o bien una potencia de 10 con $n$ d\'igitos en base 5, pero no ambas.$ Solucion: $TEX: Sea $w_p(k)$ la cantidad de digitos que posee la representacion de $10^k$ en base $p>1$. Veamos que $p^{w_p(k)-1}$ posee $w_p(k)$ cifras base $p$, y $p^{w_p(k)}$ posee $w_p(k)+1$ cifras base $p$. Luego, <br /><br />$p^{w_p(k)-1}\leq 10^k <p^{w_p(k)}$<br /><br /> O equivalentemente <br /><br />$w_p(k)-1\leq \dfrac{k}{log (p)} <w_p(k)$<br /><br />Con esto obtenemos que $w_p(k)=\displaystyle \lfloor \dfrac{k}{log(p)}\rfloor +1$ <br /><br />Supongamos que exista cierto $k$, tal que existan una potencia de $10$ con $k$ digitos base $2$ y otra potencia de $10$ con $k$ digitos base $5$. Esto es equivalente a que existen $a,b,c$ positivos tales que $w_2(a)=w_5(b)=c+1$ (donde $k=c+1$). Ocupando la formula de $w_p(n)$ deducida, la ecuacion equivale a:<br /><br />$\lfloor \dfrac{a}{log (2)}\rfloor=\lfloor \dfrac {b}{log(5)}\rfloor=c$<br /><br />Es conocido que $\lfloor x\rfloor \leq x<\lfloor x\rfloor +1$, y aplicando esto, obtenemos las dos siguientes desigualdades:<br /><br />i) $c\cdot log(2)\leq a<(c+1)\cdot log (2)$<br /><br />ii) $c\cdot log(5)\leq b<(c+1)\cdot log (5)$<br /><br />Sumando i) y ii), obtenemos que:<br /><br />$c\leq a+b<c+1\Rightarrow c=a+b$<br /><br />Reemplazando $c=a+b$ en i) y ii) obtenemos que:<br /><br />i) $(a+b)\cdot log (2)\ge a\Rightarrow b\cdot log(2)\ge a\cdot log (5)$<br /><br />ii) $(a+b)\cdot log (5)\ge b\Rightarrow a\cdot log(5)\ge b\cdot log(2)$<br /><br />De esto podemos deducir sin problemas que $a\cdot log(5)=b\cdot log (2)$ o equivalentemente, $5^a=2^b$ lo cual es imposible, pues poseen distinta paridad. Por lo tanto para cada $n$, es imposible hallar dos potencias de $10$, una con $n$ digitos base $2$ y la otra con $n$ digitos base $5$.<br /><br />$ $TEX: Solo nos resta mostrar que para cada entero $n$, existe o una potencia de $10$ con $n$ digitos base $2$ o una potencia con $n$ digitos base $5$. Nuevamente se procedera por reduccion al absurdo. Supongamos que existe un entero $n$ tal que no exista potencia de $10$ con $n$ digitos base $2$ ni potencia de $10$ con $n$ cifras base $5$. Entonces existen $r$ y $m$ tales que:<br /><br />i) $10^r<2^{k-1}<2^k<10^{r+1}$<br /><br />ii) $10^m<5^{k-1}<5^k<10^{m+1}$<br /><br />Multiplicando i) y ii) obtenemos que:<br /><br />$10^{r+m}<10^{k-1}<10^k<10^{r+m+2}$<br /><br />Estos cuatro terminos son potencias de $10$, y son distintos. Sin embargo, el intervalo $[r+m, r+m+2]$ posee $3$ enteros, y entonces al menos 2 de las 4 potencias escogidas deben ser iguales, lo cual es absurdo. Por lo tanto para cada entero $n$ existe una potencia de 10 con $n$ digitos en base $2$ o una con $n$ digitos base $5$.$ $TEX: $\boxed{Resuelto\ por\ Fatal\ Collapse}$$ Mensaje modificado por Luffy el Sep 26 2011, 11:25 PM

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 23 2008, 01:09 PM Publicado: #2
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	wena wena mi solucion pal p2 washos $TEX: \noindent Weno, este problema, en mi segundo atake, lo vi en 3 casos:\\<br /><br />Caso 1: $\triangle ABC$ acut\'angulo. Tenemos que recordar que en un tri\'angulo acut\'angulo el ortocentro y el circuncentro son interiores al tri\'angulo, por lo que la distancia entre $O$ y $H$ pertenece dentro de la circunferencia, esto significa que $OH<2R<3R\Rightarrow OH<3R$.\\<br /><br />Caso 2: $\triangle ABC$ rect\'angulo. Tenemos en este caso que el circuncentro es el punto medio de la hipotenusa y el ortocentro es el v\'ertice opuesto a la hipotenusa, por lo que $OH$ en el fondo es la mediana, igual al circunradio del tri\'angulo, que es menor que $3$ veces el mismo xD.\\<br /><br />Caso 3: $\triangle ABC$ obtus\'angulo. Tenemos que recordar que $O,G,H$ son colineales y $2OG=GH$, por lo que $OG=\frac{OH}{3}$. Ahora notemos que $G$ siempre pertenece al interior de todo tri\'angulo, por lo que $G$ est\'a dentro de su circunscrita. Entonces $OG<r\Rightarrow \frac{OH}{3}<r\Rightarrow OH<3r$, con lo que queda probado pa los $3$ casos =D!!!\\<br /><br />Weno, tambi\'en dejo la primera soluci\'on que le di, que es claramente mas corta, pero mucho mas bruta:\\<br />Por el teorema de Leibniz tenemos que $$3OG^2=AO^2+BO^2+CO^2-\frac{AB^2+BC^2+CA^2}{3}$$ $$9OG^2=9R^2-(AB^2+BC^2+CA^2)<9R^2$$ $$\left(3\cdot \frac{OH}{3}\right)^2<(3R)^2$$ $$OH<3R$$$ salu2 -------------------- $TEX: $\sqrt{5}=41$$

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 6 2008, 07:53 AM Publicado: #3
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	No conozco el "teorema de Leibniz", pero puedo comentar sobre la primera solución que pusiste. En todo triángulo se cumplen las siguientes relaciones: OH=3 OG G es interior al triángulo, y éste a su circunferencia circunscrita, por lo tanto OG<r (circunradio). Multiplicando por 3, se concluye que OH=3 OG<3r Básicamente la misma solución de pelao malo, pero quería destacar que la separación de casos no era necesaria. -------------------- Sebastián Elías Puelma Moya Administrador FMAT

~Fatal_Collapse~ Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 7 2009, 07:42 PM Publicado: #4
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.564 Registrado: 12-November 07 Desde: La Union, XIV Region de los Rios Miembro Nº: 12.607 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	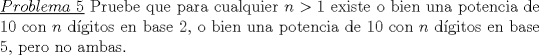CITA(Luffy @ Oct 17 2007, 08:44 PM) $TEX: \noindent \underline{$Problema\ 5$} Pruebe que para cualquier $n>1$ existe o bien una potencia de 10 con $n$ d\'igitos en base 2, o bien una potencia de 10 con $n$ d\'igitos en base 5, pero no ambas.$ Aqui va una parte del problema $TEX: Sea $w_p(k)$ la cantidad de digitos que posee la representacion de $10^k$ en base $p>1$. Veamos que $p^{w_p(k)-1}$ posee $w_p(k)$ cifras base $p$, y $p^{w_p(k)}$ posee $w_p(k)+1$ cifras base $p$. Luego, <br /><br />$p^{w_p(k)-1}\leq 10^k <p^{w_p(k)}$<br /><br /> O equivalentemente <br /><br />$w_p(k)-1\leq \dfrac{k}{log (p)} <w_p(k)$<br /><br />Con esto obtenemos que $w_p(k)=\displaystyle \lfloor \dfrac{k}{log(p)}\rfloor +1$ <br /><br />Supongamos que exista cierto $k$, tal que existan una potencia de $10$ con $k$ digitos base $2$ y otra potencia de $10$ con $k$ digitos base $5$. Esto es equivalente a que existen $a,b,c$ positivos tales que $w_2(a)=w_5(b)=c+1$ (donde $k=c+1$). Ocupando la formula de $w_p(n)$ deducida, la ecuacion equivale a:<br /><br />$\lfloor \dfrac{a}{log (2)}\rfloor=\lfloor \dfrac {b}{log(5)}\rfloor=c$<br /><br />Es conocido que $\lfloor x\rfloor \leq x<\lfloor x\rfloor +1$, y aplicando esto, obtenemos las dos siguientes desigualdades:<br /><br />i) $c\cdot log(2)\leq a<(c+1)\cdot log (2)$<br /><br />ii) $c\cdot log(5)\leq b<(c+1)\cdot log (5)$<br /><br />Sumando i) y ii), obtenemos que:<br /><br />$c\leq a+b<c+1\Rightarrow c=a+b$<br /><br />Reemplazando $c=a+b$ en i) y ii) obtenemos que:<br /><br />i) $(a+b)\cdot log (2)\ge a\Rightarrow b\cdot log(2)\ge a\cdot log (5)$<br /><br />ii) $(a+b)\cdot log (5)\ge b\Rightarrow a\cdot log(5)\ge b\cdot log(2)$<br /><br />De esto podemos deducir sin problemas que $a\cdot log(5)=b\cdot log (2)$ o equivalentemente, $5^a=2^b$ lo cual es imposible, pues poseen distinta paridad. Por lo tanto para cada $n$, es imposible hallar dos potencias de $10$, una con $n$ digitos base $2$ y la otra con $n$ digitos base $5$.<br /><br />$ Aqui va la parte final (tan sencilla y me costo caleta darme cuenta xD) $TEX: Solo nos resta mostrar que para cada entero $n$, existe o una potencia de $10$ con $n$ digitos base $2$ o una potencia con $n$ digitos base $5$. Nuevamente se procedera por reduccion al absurdo. Supongamos que existe un entero $n$ tal que no exista potencia de $10$ con $n$ digitos base $2$ ni potencia de $10$ con $n$ cifras base $5$. Entonces existen $r$ y $m$ tales que:<br /><br />i) $10^r<2^{k-1}<2^k<10^{r+1}$<br /><br />ii) $10^m<5^{k-1}<5^k<10^{m+1}$<br /><br />Multiplicando i) y ii) obtenemos que:<br /><br />$10^{r+m}<10^{k-1}<10^k<10^{r+m+2}$<br /><br />Estos cuatro terminos son potencias de $10$, y son distintos. Sin embargo, el intervalo $[r+m, r+m+2]$ posee $3$ enteros, y entonces al menos 2 de las 4 potencias escogidas deben ser iguales, lo cual es absurdo. Por lo tanto para cada entero $n$ existe una potencia de 10 con $n$ digitos en base $2$ o una con $n$ digitos base $5$.$ Nota: se ocupo el logaritmo en base 10 -------------------- Ricardo Vargas Obando Ex-alumno Deutsche Schule La Unión (Generación 2010, de los 150 años). Novato de Licenciatura en Matemática/Estadística, en la Pontificia Universidad Católica de Chile. Grupo de facebook de Novatos Matemática y Estadística PUC 2011 Currículum Olímpico: Medalla de Plata, XIX Olimpiada Nacional de Matemática Nivel Menor (2007) Medalla de Oro, XXI Olimpiada Nacional de Matemática Nivel Mayor (2009) Medalla de Bronce, XXV Olimpiada Iberoamericana de Matemática (2010) Medalla de Oro, XXII Olimpiada Nacional de Matemática Nivel Mayor (2010) "What we learned as children, that one plus one equals two, we know to be false. One plus one equals one. We even have a word when you plus another, equals one. That word is love." "Todos piensan en cambiar el mundo, pero nadie piensa en cambiarse a sí mismo."

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 26 2011, 11:24 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Kain #13 @ Nov 7 2009, 08:42 PM) Aqui va una parte del problema $TEX: Sea $w_p(k)$ la cantidad de digitos que posee la representacion de $10^k$ en base $p>1$. Veamos que $p^{w_p(k)-1}$ posee $w_p(k)$ cifras base $p$, y $p^{w_p(k)}$ posee $w_p(k)+1$ cifras base $p$. Luego, <br /><br />$p^{w_p(k)-1}\leq 10^k <p^{w_p(k)}$<br /><br /> O equivalentemente <br /><br />$w_p(k)-1\leq \dfrac{k}{log (p)} <w_p(k)$<br /><br />Con esto obtenemos que $w_p(k)=\displaystyle \lfloor \dfrac{k}{log(p)}\rfloor +1$ <br /><br />Supongamos que exista cierto $k$, tal que existan una potencia de $10$ con $k$ digitos base $2$ y otra potencia de $10$ con $k$ digitos base $5$. Esto es equivalente a que existen $a,b,c$ positivos tales que $w_2(a)=w_5(b)=c+1$ (donde $k=c+1$). Ocupando la formula de $w_p(n)$ deducida, la ecuacion equivale a:<br /><br />$\lfloor \dfrac{a}{log (2)}\rfloor=\lfloor \dfrac {b}{log(5)}\rfloor=c$<br /><br />Es conocido que $\lfloor x\rfloor \leq x<\lfloor x\rfloor +1$, y aplicando esto, obtenemos las dos siguientes desigualdades:<br /><br />i) $c\cdot log(2)\leq a<(c+1)\cdot log (2)$<br /><br />ii) $c\cdot log(5)\leq b<(c+1)\cdot log (5)$<br /><br />Sumando i) y ii), obtenemos que:<br /><br />$c\leq a+b<c+1\Rightarrow c=a+b$<br /><br />Reemplazando $c=a+b$ en i) y ii) obtenemos que:<br /><br />i) $(a+b)\cdot log (2)\ge a\Rightarrow b\cdot log(2)\ge a\cdot log (5)$<br /><br />ii) $(a+b)\cdot log (5)\ge b\Rightarrow a\cdot log(5)\ge b\cdot log(2)$<br /><br />De esto podemos deducir sin problemas que $a\cdot log(5)=b\cdot log (2)$ o equivalentemente, $5^a=2^b$ lo cual es imposible, pues poseen distinta paridad. Por lo tanto para cada $n$, es imposible hallar dos potencias de $10$, una con $n$ digitos base $2$ y la otra con $n$ digitos base $5$.<br /><br />$ Aqui va la parte final (tan sencilla y me costo caleta darme cuenta xD) $TEX: Solo nos resta mostrar que para cada entero $n$, existe o una potencia de $10$ con $n$ digitos base $2$ o una potencia con $n$ digitos base $5$. Nuevamente se procedera por reduccion al absurdo. Supongamos que existe un entero $n$ tal que no exista potencia de $10$ con $n$ digitos base $2$ ni potencia de $10$ con $n$ cifras base $5$. Entonces existen $r$ y $m$ tales que:<br /><br />i) $10^r<2^{k-1}<2^k<10^{r+1}$<br /><br />ii) $10^m<5^{k-1}<5^k<10^{m+1}$<br /><br />Multiplicando i) y ii) obtenemos que:<br /><br />$10^{r+m}<10^{k-1}<10^k<10^{r+m+2}$<br /><br />Estos cuatro terminos son potencias de $10$, y son distintos. Sin embargo, el intervalo $[r+m, r+m+2]$ posee $3$ enteros, y entonces al menos 2 de las 4 potencias escogidas deben ser iguales, lo cual es absurdo. Por lo tanto para cada entero $n$ existe una potencia de 10 con $n$ digitos en base $2$ o una con $n$ digitos base $5$.$ Nota: se ocupo el logaritmo en base 10 Excelente, una solucion notable Saludos

« Posterior · Olimpiada Asia-Pacifico · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 3rd April 2025 - 09:25 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.