|
|
|
|
|
|
|
  |
 Dec 21 2005, 01:34 PM Dec 21 2005, 01:34 PM
Publicado:
#1
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
Bueno esta la saqué de otro foro.
No sé ni quien es goldbach ni nada. Pero tal vez alguien más en este foro se pueda entretener tratando de demostrar la conjetura. (sorry si ya estaba, no me di el tiempo de buscarla, como buen chileno Dice asi: Todo número par mayor que 4 puede ser escrito como suma de dos primos impares. Bueno si alguien la demuestra y se hace millonario o algo me menciona -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Dec 22 2005, 10:34 AM Dec 22 2005, 10:34 AM
Publicado:
#2
|
|
 Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 725 Registrado: 17-July 05 Desde: Puente Alto-Santiago Miembro Nº: 148 Nacionalidad:  Universidad:  Sexo:  |
tengo una duda de conceptos, si alguien me aclara plz
Conjetura significa algo que es cierto, y se cumple para todo numero de la regla, pero que no ha sido aun demostrado. eso es?? Saludos Gracias Dex! -------------------- "Resolver un problema es una meta específica de la inteligencia e inteligencia es el don específico de los seres humanos: Resolver un problema es la actividad humana por excelencia"
  |
|
|
|
| Cesarator |
 Dec 22 2005, 11:09 AM Dec 22 2005, 11:09 AM
Publicado:
#3
|
|
Invitado |
Conjetura se usa en matemáticas para indicar algo que aparentemente es cierto, pero que no se ha podido demostrar ni desmentir. Se trata de afirmaciones que cualquiera puede hacer (algunas más interesantes que otras), y que está pendiente decidir si es cierta o falsa. La historia de la matemática está llena de "conjeturas" que terminaron siendo verdaderas, y otras que se desmintieron. La conjetura de Goldbach es famosa, de hecho hay un libro que hace referencia a ella "El tio Petros y la conjetura de Goldbach ". Ver link AQUI Actualmente, algunas conjeturas famosas son la Conjetura de Riemann (la más famosa de la matemática, que tiene que ver con la distribución de los números primos), la Conjetura de Poincaré (Sobre la deformación de superficies conexas en esferas), El problema P v/s NP, etc. Estas tres que menciono son 3 de los 7 "Problemas del Milenio", que fueron dotados a finas de 1999 con un premio de 1 millón de dólares cada uno para el q que los "resuelva", donde resolver significa demostrar o desmentir la conjetura respectiva. La conjetura de Goldbach tenía un premio de 100.000 dólares otorgado por la editorial del libro de arriba, pero era con plazo y nadie la resolvió, así que fue declarado desierto. Una anécdota sobre el matemático G. Hardy dice que, una vez que viajaba a EEUU (desde inglaterra) en Barco (le tenía miedo a los viajes), dejó un mensaje al partir su crucero que decía más o menos lo que sigue: " Encontré una demostración para la conjetura de Riemann!! Sin embargo, debo tomar el barco y no puedo decirla ahora" Según Hardy, esa nota era como un seguro de vida, pues "Dios" no permitiría que el barco naufragara y el pasara a la historia como el que resolvió la conjetura sin poder dar la solución.... |
|
|
|
| Cesarator |
 Dec 22 2005, 11:18 AM Dec 22 2005, 11:18 AM
Publicado:
#4
|
|
Invitado |
El libro del tio petros está en la librería antartica!! Y a un precio razonable. Hace tiempo que quería leerlo. Me lo han recomendado mucho, y ahora voy a comprarlo. Ese libro ha ganado varios premios y me atrevo a recomendarlo aunque no lo he leido. Después de leerlo daré una recomendación más objetiva
Ojalá esté en stck en Concepción. Ver link AQUI PS Lo recomiendo como regalo de Navidad PS2: Seguramente el tío Petros era amigo del famosísimo abuelo Anacleto. Voy a preguntarle cuando lo vea |
|
|
|
 Dec 22 2005, 12:46 PM Dec 22 2005, 12:46 PM
Publicado:
#5
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
Otra "Ex Conjetura" Famosa es la conocida conjetura de Fermat, que dice... o decía ( no sé... supongo que es relativo ): [b]Si n es un número natural mayor que 2, no existe ningún trío de números enteros positivos a,b y c, que satisfagan
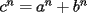 Entonces la famosa historia cuenta que esto lo descubrió mientras leía el libro "Aritmética" de Diofanto, y en su margen escribió algo así como: "he encontrado una maravillosa demostración para este hecho, pero es muy larga como para caber en el margen de este libro". Pasaron más de 300 años sin que se resolviera. Recientemente un matemático británico llamado Andrew Wiles anunció que tenía la demostración de otra conjetura llamada de Shimura-Taniyama-Weil. Con esta demostración era posible demostrar la conjetura de Fermat. En 1995 Wiles publica su demostración, de aqui la conjetura de Fermat pasó a llamarse GRAN TEOREMA DE FERMAT =o -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 14 2006, 01:59 PM Feb 14 2006, 01:59 PM
Publicado:
#6
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 40 Registrado: 14-February 06 Miembro Nº: 568 |
CITA(Cesarator @ Dec 22 2005, 02:18 PM) El libro del tio petros está en la librería antartica!! Y a un precio razonable. Hace tiempo que quería leerlo. Me lo han recomendado mucho, y ahora voy a comprarlo. Ese libro ha ganado varios premios y me atrevo a recomendarlo aunque no lo he leido. Después de leerlo daré una recomendación más objetiva Ojalá esté en stck en Concepción. Ver link AQUI PS Lo recomiendo como regalo de Navidad PS2: Seguramente el tío Petros era amigo del famosísimo abuelo Anacleto. Voy a preguntarle cuando lo vea yo habia escuchado que se probo pero con computadores, no con demostraciones elegantes |
|
|
|
| Cesarator |
 Feb 14 2006, 03:07 PM Feb 14 2006, 03:07 PM
Publicado:
#7
|
|
Invitado |
Con respecto al libro del tía petros, es bastante bueno y lo recomiendo. Ya lo leí. Además es barato, así que a comprarlo!
Ahora, la conjetura no se ha demostrado. También he escuchado "rumores" sobre demostraciones "hechas por computadores". Incluso a matemáticos los he escuchado hablar con aires de misterio de esas demostraciones y de como los computadores ya hacen demostraciones. Hace un tiempo investigué sobre tal tema y confirmé lo que sospechaba, es inconcebible que un computador "haga demostraciones". La conjetura de Goldbach sigue sin una demostración. Lo que han hecho los computadores es verificarla como cierta para una cantidad muy grande de números, digamos para 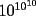 , pero es imposible que logren verificarla para todos los números, por el simple hecho que son infinitos. Ahora, nosotros podemos encontrar ese número muy grande, pero al compararlo con infinito es lo mismo que 2 o 3. Es decir, al lado de infinito da lo mismo 10 millones de millones que 1. , pero es imposible que logren verificarla para todos los números, por el simple hecho que son infinitos. Ahora, nosotros podemos encontrar ese número muy grande, pero al compararlo con infinito es lo mismo que 2 o 3. Es decir, al lado de infinito da lo mismo 10 millones de millones que 1.Ahora, lo que ha dado origen al rumor de "demostraciones por computadores" es la demostración de otro problema famoso, que era "El problema de los cuatro colores". Se pedía demostrar que todo "mapa" puede colorearse usando sólo 4 colores (bajo ciertas restricciones). Esa demostración efectivamente fue hecha por compùtadores, pero ¿Cómo?. El asunto es bastante secillo. Resulta que alguien observó que la demostración se subdivide en, digamos, 500 casos distintos, y verificar cada caso toma alrededor de 1 año. Lo que hizo esta persona fue realizar un programa que verificó cada uno de los 500 casos en un par de meses. Esa tarea le tomaría a un humano siglos, pero el computador, que obviamente es más rápido para hacer cálculos, se demoró un par de meses. En fin, se trataba entonces de una demostración muy muy "fatigosa", que de no ser por la gran capacidad de cálculo del computador no habría podido realizarse, pero que ya está hecha. Y NADA QUE VER conque el computador haya "descubierto la demostración " o "razonado", sólo hizo lo que hace muy bien: muchos cálculos muy rápido. |
|
|
|
 Feb 14 2006, 09:47 PM Feb 14 2006, 09:47 PM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad:  Colegio/Liceo:  Sexo:  |
CITA(Gazoo @ Dec 22 2005, 02:46 PM) Otra "Ex Conjetura" Famosa es la conocida conjetura de Fermat, que dice... Sobre esta conjetura escribí algo aquí, como resumen de una traducción de un sitio web allí indicado. Hoy podría darse como un teorema, supongo. Porque Andrew Wiles juró, siendo chico (por los años '60 si mi memoria no falla... pregúntenle al abuelo Anacleto), que demostraría el teorema. Cumplió, parece que no a la primera, en 1995, efectivamente demostrando un resultado más general e invocando curvas elípticas. Se supone que Fermat no tenía idea de toda esa matemática. Nadie de la época, se supone. ¿Cómo pudo Fermat intuirlo?Otro detalle... por ahí escuché una vez (no revelaré mi fuente) que la demostración de Wiles tenía como 2000 páginas y que no estaría revisada del todo. una traba son las 2000 páginas, otra es que haya gente competente para calificar esta demostración. Supongo que pasa siempre que hay un teorema con demostración tan complicada o sea... un paper de 2000 páginas... ningún margen de libro aguanta... o Fermat tenía una demostración más breve, o se llevó el secreto a la tumba para desafiar a la comunidad matemática, o definitivamente su "demostración" estaba errada CITA(Cesarator @ Feb 14 2006, 05:07 PM) Con respecto al libro del tía petros, es bastante bueno y lo recomiendo. Ya lo leí. Además es barato, así que a comprarlo! Y yo que pensaba, que Cesarator era el autor de ese libro... o al menos que ya lo tenía en su biblioteca... ya me imaginaba al tío Petros discutiendo sus ideas con el abuelo Anacleto... CITA(Cesarator @ Feb 14 2006, 05:07 PM) Ahora, lo que ha dado origen al rumor de "demostraciones por computadores" es la demostración de otro problema famoso, que era "El problema de los cuatro colores". Te cuento lo que averigüé al respecto, porque durante el año pasado usé Saint Se pedía demostrar que todo "mapa" puede colorearse usando sólo 4 colores (bajo ciertas restricciones). Esa demostración efectivamente fue hecha por compùtadores, pero ¿Cómo?. El asunto es bastante secillo. Resulta que alguien observó que la demostración se subdivide en, digamos, 500 casos distintos, y verificar cada caso toma alrededor de 1 año. Lo que hizo esta persona fue realizar un programa que verificó cada uno de los 500 casos en un par de meses. Esa tarea le tomaría a un humano siglos, pero el computador, que obviamente es más rápido para hacer cálculos, se demoró un par de meses. La solución original del problema data de 1976, hecha efectivamente por un PC (o, imagino yo, una red de PC's). No se trataría precisamente de demostrar el teorema para casos pequeños, sino en general. Aunque para esto evaluaron 1476 grafos, esos eran sus casos pariculares. Un "avance" se consiguió en 1994, reduciendo el número de casos a 633 y optimizando otros aspectos. Para quien prende velitas a Saint Esto de ocupar computadoras, o varias conectadas simultáneamente gracias a Internet, para resolver problemas... hoy en día es "grito y plata" para la resolución de algunos problemas no matemáticos, como por ejemplo la búsqueda de una cura para el SIDA. Y los matemáticos se siven de esto, conectando como 200000 computadores para buscar números primos de Mersenne... ese es otro tema, uno busca primos de Mersenne, bien grandotes, un poco por ego, pero es prácticamente la única familia de números que se deja "desnudar" (en materia de primalidad) de manera eficiente, por ejemplo con el test de Lucas-Lehmer. Y los números primos grandotes sirven, aunque no entiendo cómo, para criptografía, para seguridad en Internet, por ejemplo A fin de cuentas, no es malo conectar hartos computadores para resolver un problema grandote... lo digo, porque esta metodología tiene sus detractores, o bien hay gente que no entiende para qué se hacen estas cosas Una vez + me fui en la volada, y + encima estoy fuera del sector de jugoseo Pero lo que he dicho, es verdad... ...y no puedo olvidar decir esto: los profesores + buenos que he tenido, sobre todo en la universidad, son aquellos que pueden sacar la tensión de una clase cualquiera y empezar a contar anécdotas de este tipo, o revelar a sus alumnos los detalles más interesantes, copuchas que han escuchado, etc... todo eso cuando lo combinan con una gran calidad pedagógica (Cloruro de Sodio)$#$%"#$#&%$#&%$&%#$"%$&% -------------------- |
|
|
|
 Nov 20 2013, 12:38 PM Nov 20 2013, 12:38 PM
Publicado:
#9
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 17-November 13 Miembro Nº: 124.639 Sexo:  |
Antes de que lo lea nadie más diré que lo que digo a continuación esta mal, falla en que un primo puede cubrir más de una posibilidad(varios primos, entre 5 y 11 hay un multiplo de 3)
Intentaré responder a esta conjetura para ver que fallos me sacan. Conjetura fuerte de Goldbach. (Lo escribiré con ejemplos numericos para simplificar su lectura) 1.Supongamos un número 2N, donde N no es divisible entre algun primo, al restarle ese primo, el número resultante no será divisible entre ese primo ni entre ninguno comprendido en N. Ejemplo: Supongamos el número 2*3*5*7*13 este número no es divisible entre 11, entonces 2*3*5*7*13-11 no será divisible entre 11(porque 2*3*5*7 no lo es), ni entre ninguno de los considerados (porque la distancia de 2*3*5*7*13 hasta 2*3*5*7*13-11 es un primo no incluido en 2*3*5*7*13). Si solo hubiese ese primo (entre 1 y N) sin considerar, estaría resuelto. 2.Pero, ¿podría ser divisible entre alguno no considerado? Bien, en ese caso, supongamos que existen dos y solo dos primos no considerados. Añadamos el 17: Al añadirle, o bien cuadraba con el numero 2*3*5*7*13-11 o no. Si no cuadraba estaría resuelto. Si cuadraba, 2*3*5*7*13-17 no será divisible entre 17, ni tampoco de los incluidos en 2*3*5*7*13, supongamos que no es multiplo de 11, estaría resuelto. Si 2*3*5*7*13-11 es divisible entre 17 y 2*3*5*7*13-17 es divisible entre 11: Nos daría error, pero hay que tener en cuenta una cosa, el número 2*3*5*7*13-1 no es divisible entre ninguno de los incluidos en 2*3*5*7*13 y si 2*3*5*7*13-11 es divisible entre 17 y 2*3*5*7*13-17 es divisible entre 11, 2*3*5*7*13-1 no puede serlo entre 11 ni entre 17. 3.Hasta aqui la exposición de mis argumentos porque sería alargarlo demasiado. ¿Se puede decir que estoy en lo cierto para casos en los que falten más de tres primos no incluidos en el par considerado? En mi opinión si, pero suelo confundirme con frecuencia. Añadiré algo más: Al introducir un nuevo primo(19), cumplirá siempre para alguno de los casos: Si esta en 2*3*5*7*13-11, no puede estar en ninguno de los otros casos y como ahora tengo el 2*3*5*7*13-19, contrarestaría el caso que cubro y asi para cada nuevo primo. Voy ha añadir esto aparte(esto creo que esta bien): Con este método se puede conseguir un primo, basta con multiplicar primos seguidos a excepción de uno de ellos y despues restarle ese primo elevado a un natural mayor que 1 y que el resultado este por debajo del siguiente primo de la succesion al cuadrado. Gracias por la lectura, Luckdevil7. Mensaje modificado por Luckdevil7 el Nov 25 2013, 01:10 PM |
|
|
|
 Nov 22 2013, 12:01 AM Nov 22 2013, 12:01 AM
Publicado:
#10
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 17-November 13 Miembro Nº: 124.639 Sexo:  |
Buenos días, lo primero que diré es que no soy matemático, pero cuanto más pienso en este probema más me obsesiona, tengo más ideas pero todas me llevan a problemas que no soy capaz de resolver. Ahí va mi pregunta:
------1---3--5----7---11--13--17--19--23--29--31--37 ... -1----2---4--6----8--12--14--18--20--24--30--32--38 -3----4---6--8---10--14--16--20--22--26--32--34--40 -5----6---8-10---12--16--18--22--24--28--34--36--42 -7----8--10--12--14--18--20--24--26--30--36--38--44 11---12--14--16--18--22--24--28--30--34--40--42--48 13---14----------------------26--30--32--36--42--44--50 17---18---------------------------34--36--40--46--48--54 19---20--------------------------------38--42--48--50--56 23---24-------------------------------------46--52--54--60 29---30------------------------------------------58--60--66 31---32 37---38 ... Esta es una tabla en la que aparecen la suma de primos, en ella hay propiedades de distancia, por ejemplo: la distancia (1,2), (4,2) = la distancia (1,4),(4,4), es decir, viendolo como si fueran cuadrados y su camino va cambiando igual. Pero también es simetrica con respecto la diagonal. Y tambien, por ejemplo del 22 de la diagonal hasta el 34 de su linea, va cambiando igual que del mismo 34 hasta el 46 de su columna y al reevés y así para todo. Estos movimientos son acumulativos para cada número, es decir, si desde el 34 de la diagonal hasta el 54 de su fila hay 20 unidades, para cada uno de los valores 36, 40, 46, 48 se pueden consegir valores a 20 unidades por simetría. ¿Se puede de alguna forma establecer una fórmula sencilla que cumpla estas propiedades a medida que vaya añadiendo números?(El libro de algebra se me cayó a la basura cuando era pequeño y tampoco a quedado muy recto, use un boli a modo de regla) ¿Habría forma de decir que cubre todos los valores pares si la distancia entre primos crece a tal velocidad? Mensaje modificado por Luckdevil7 el Nov 22 2013, 12:21 AM |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:42 AM |










