|
|
|
|
|
|
|
  |
| Cesarator |
 Dec 20 2005, 03:51 PM Dec 20 2005, 03:51 PM
Publicado:
#1
|
|
Invitado |
Voy a postear algunos de los problemas que aparecieron en esta revista. Si alguien los resuelve antes del 1 de MArzo 2006, lo envía (lo ayudo a hacerlo) a la revista y se hace mundialmente famoso como uno de los "solvers" para estos problemas.
Todos invitados a participar. Problema 1726: Sean 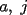 enteros positivos con enteros positivos con 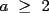 . .Demostrar que existe un entero positivo  tal que tal que 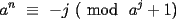 si y solo si si y solo si 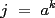 para algun para algun 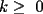 . .Problema 1728: Sea 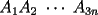 un poligono regular de 3n lados y sea P un punto en el arco menor un poligono regular de 3n lados y sea P un punto en el arco menor 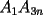 de su circunferencia circunscrita. Demostrar que de su circunferencia circunscrita. Demostrar que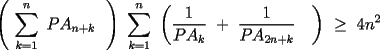 . .Problema 1729: Para cada entero positivo k, sea 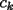 el producto de los primeros k enteros positivos impares, con el producto de los primeros k enteros positivos impares, con 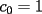 . Probar que para cada entero no negativo n. . Probar que para cada entero no negativo n.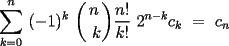 . .
|
|
|
|
 Feb 5 2006, 07:26 PM Feb 5 2006, 07:26 PM
Publicado:
#2
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Problema 1729: Para cada entero positivo k, sea
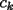 el producto de los primeros k enteros positivos impares, con el producto de los primeros k enteros positivos impares, con 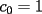 . Probar que para cada entero no negativo n. . Probar que para cada entero no negativo n.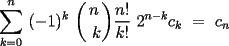 Solucion: Definamos 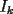 y y 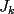 de la siguiente manera: de la siguiente manera: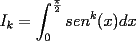 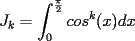 Notemos que 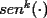 y y 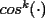 son integrables en el intervalo son integrables en el intervalo ![TEX: $\left[0,\frac{\pi}{2}\right]$](./tex/25937.gif) pues ambas son funciones continuas en ese intervalo. pues ambas son funciones continuas en ese intervalo.Lema 1: 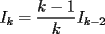 para para 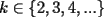 Demostracion: Usando integracion por partes con 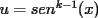 y y 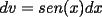 tendremos que: tendremos que:![TEX: $\displaystyle I_k=\int_{0}^{\frac{\pi}{2}}sen^k(x)dx=\underbrace{\left. sen^{k-1}(x)(-cos(x))\right]_{0}^{\frac{\pi}{2}}}_{\displaystyle 0}-\underbrace{\int_{0}^{\frac{\pi}{2}}(-cos(x))(k-1)sen^{k-2}(x)cos(x)dx}_{\displaystyle -(k-1)\int_{0}^{\frac{\pi}{2}}sen^{k-2}(x)cos^2(x)dx}$](./tex/25946.gif) 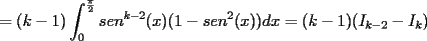 De esta identidad se comcluye el lema de manera directa. Lema 2: 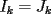 para para 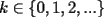 Demostracion: Basta usar el cambio de variables 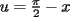 y el hecho de que y el hecho de que 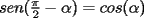 . .Usando el Lema 1 reiteradas veces, podemos concluir que: 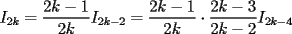 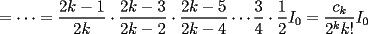 [ Es claro que [ Es claro que  ] ]Usando esto concluiremos nuestro siguiente lema: Lema 3: 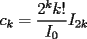 para para 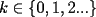 Demostracion: Para 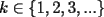 se sigue la demostracion hecha previamente. se sigue la demostracion hecha previamente.Para 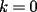 debemos testear la propiedad "a mano" debemos testear la propiedad "a mano"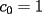 [por enunciado] y [por enunciado] y 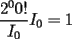 [Ojo que [Ojo que 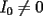 ] ]Q.E.D. Reemplazando en nuestra sumatoria tendremos que: 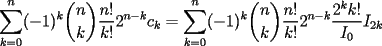 ![TEX: $\displaystyle =\frac{2^n n!}{I_0}\sum_{k=0}^n (-1)^k {n\choose k}I_{2k}=\displaystyle =\frac{2^n n!}{I_0}\sum_{k=0}^n \left[ (-1)^k {n\choose k}\left[ \int_{0}^{\frac{\pi}{2}}sen^{2k}(x)dx\right] \right]$](./tex/26044.gif) ![TEX: $\displaystyle =\frac{2^n n!}{I_0}\sum_{k=0}^n \int_{0}^{\frac{\pi}{2}}{n\choose k}(-1)^k sen^{2k}(x)dx=\frac{2^n n!}{I_0}\int_{0}^{\frac{\pi}{2}}\left[\sum_{k=0}^n {n\choose k}(-sen^{2}(x))^k \right] dx$](./tex/26092.gif) 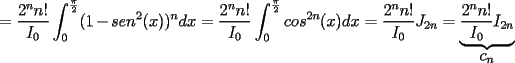 Asi queda demostrada la proposicion -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 5 2006, 08:55 PM Feb 5 2006, 08:55 PM
Publicado:
#3
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo:  Universidad:  Sexo:  |
Con esto si que se le haria buena propaganda a Fmat Mensaje modificado por Gazoo el Mar 8 2013, 01:05 PM -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein.   Estudiante Ingeniería Civil Eléctrica - DIE USACH |
|
|
|
 Feb 5 2006, 08:59 PM Feb 5 2006, 08:59 PM
Publicado:
#4
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 26-May 05 Desde: Santiago Miembro Nº: 58 |
Nose que decir simplemente una exelente solucion.....DEMASIADO HERMOSA....
ESTOY ALUSINANDO |
|
|
|
 Feb 5 2006, 09:21 PM Feb 5 2006, 09:21 PM
Publicado:
#5
|
|
|
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 30-January 06 Miembro Nº: 525 |
maestro
|
|
|
|
 Feb 5 2006, 09:59 PM Feb 5 2006, 09:59 PM
Publicado:
#6
|
|
|
Matemático Grupo: Usuario FMAT Mensajes: 37 Registrado: 6-August 05 Desde: Chile xD Rancagua Miembro Nº: 175 |
ahhhhhhhh.... que buena david
--------------------  El genio es un uno por ciento de inspiración y un noventa y nueve por ciento de transpiración. [Thomas Alba Edison] |
|
|
|
 Feb 5 2006, 10:34 PM Feb 5 2006, 10:34 PM
Publicado:
#7
|
|
|
Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad:  Sexo:  |
Problema 1728: Sea
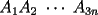 un poligono regular de 3n lados y sea P un punto en el arco menor un poligono regular de 3n lados y sea P un punto en el arco menor 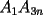 de su circunferencia circunscrita. Demostrar que de su circunferencia circunscrita. Demostrar que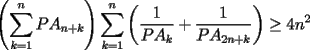 Solucion: Para simplificar un poco las notaciones llamemos: 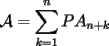 y 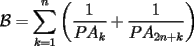 Luego se nos pide probar que 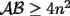 Ahora podemos comenzar: Probemos previamente la siguiente propiedad Lema Consideremos una circunferencia y tres puntos de ella tales que 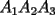 sea un triangulo equilatero(ver figura). Si sea un triangulo equilatero(ver figura). Si 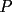 es un punto en el arco menor es un punto en el arco menor 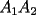 , entonces , entonces 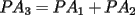  Demostracion: Si aplicamos el Teorema de Ptolomeo al cuadrilatero 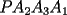 tendriamos que: tendriamos que: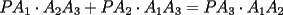 pero como 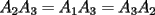 entonces al simplificar la expresion anterior obtendremos que: entonces al simplificar la expresion anterior obtendremos que: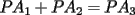 Consideremos ahora el poligono regular de "3n lados" del enunciado. Notemos que cada "n lados" tendremos un arco barrido de 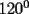 (pues con los 3n lados barrimos 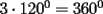 ) )Luego el arco menor entre 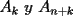 sera de sera de 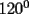 . Asi tambien lo sera el arco entre . Asi tambien lo sera el arco entre 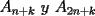 y entre y entre 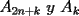 ( este ultimo pues si estamos dando la vuelta completa y llevamos ( este ultimo pues si estamos dando la vuelta completa y llevamos 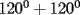 , nos faltan , nos faltan 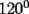 para llegar al punto de partida ) para llegar al punto de partida )Luego si aplicamos nuestra propiedad demostrada en el lema a los puntos 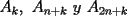 con el punto con el punto  ( del enunciado ) en el arco menor ( del enunciado ) en el arco menor 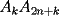 tendriamos que: tendriamos que: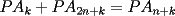 Si aplicamos este criterio para 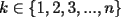 ( notar que para estos valores de k tenemos la certeza de que ( notar que para estos valores de k tenemos la certeza de que 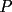 pertenece al arco menor pertenece al arco menor 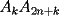 ) tendremos que: ) tendremos que: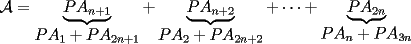 Por otro lado: 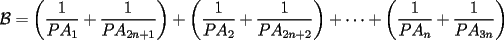 Luego aplicando la desigualdad 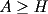 para los siguientes "2n medidas" reales positivas: para los siguientes "2n medidas" reales positivas: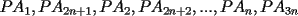 se concluye que: 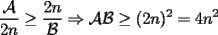 que era lo que se pedia probar PD: Por ahi alguien me pregunto a que me referia con arco menor. La respuesta es que si hablo del arco menor AB, nosotros tenemos dos arcos en la circunferencia que conectan A con B, uno grande y uno chico. Yo me refiero al mas chico..jejejeje -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!)
Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)   |
|
|
|
 Feb 5 2006, 11:50 PM Feb 5 2006, 11:50 PM
Publicado:
#8
|
|
 Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 178 Registrado: 28-May 05 Desde: Aca , alla , aca , alla Miembro Nº: 70 Nacionalidad:  Universidad:  Sexo:  |
Todavia no logro entender nada , pero se nota q david le pega demasiado , pobre matematica va a quedar botada y noqueada tanto q le pegay david!!!
-------------------- Por un lado la matematica , lo mas importante , pero por el otro el basquetbol y ginobili lo mejor q hay!!!!
Team Naranja!!! Apagando incendios xD    |
|
|
|
 Feb 6 2006, 12:04 AM Feb 6 2006, 12:04 AM
Publicado:
#9
|
|
 Matemático Grupo: Usuario FMAT Mensajes: 55 Registrado: 26-May 05 Desde: Santiago Miembro Nº: 58 |
Demaciado top las dos soluciones. Aunque admito me costo mucho mas entender la segunda que la primera... Completamente excelente tus soluciones david.
YA CASI LISTO EL DESAFIO PARA MARZO....DURO UN DIA.... |
|
|
|
| Cesarator |
 Feb 6 2006, 06:46 PM Feb 6 2006, 06:46 PM
Publicado:
#10
|
|
Invitado |
bien
Lamentablemente, no seguiré posteando los problemas de la MAGAZINE, pues son con copyright... NO!!!... acabo de leer con atención y si se puede reproducir el material de la MAGAZINE siempre que no sea con fines comerciales y se ponga el copyright, que lo pongo ahora. Los problemas de arriba son: Copyright the Mathematical Association of America 2005. All rights reserved. |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 3rd April 2025 - 10:42 AM |









