Un resultado de Riemann - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Ejercitación > Desafíos

Reply to this topic

Start new topic

Un resultado de Riemann, series

Cesarator	Dec 28 2005, 04:36 PM Publicado: #1
Invitado	$TEX: B. Riemann fue tal vez uno de los matematicos ``modernos'' de mayor genio. Todo estudiante universitario se ha topado con las llamadas ``sumas de Riemann'' para definir las integrales definidas, y seguramente el problema pendiente m\'as famoso de la matem\'atica actualmente es la llamada ``conjetura de Riemann'', sobre los ceros de la llamada funci\'on zeta de Riemann. Esta conjetura est\'a relacionada con el problema de la distribuci\'on de los n\'umeros primos.<br /><br />Un llamativo resultado descubierto por Riemann es el siguiente. Decimos que una serie<br />$$<br />\sum a_n<br />$$<br />es {\bf absolutamente convergente} si $\sum \|a_n\|$ es convergente, y que es {\bf condicionalmente convergente} si $\sum a_n$ converge, pero $\sum \|a_n\|$ diverge a infinito. <br /><br />El ejemplo tipico de serie condicionalmente convergente es la serie<br />$$<br />\sum_{n=1}^\infty \frac{(-1)^n}{n}.<br />$$<br /><br />Ahora, un {\bf reordenamiento} de los naturales es una funci\'on $\sigma :\mathcal N \to \mathcal N$ que sea biyectiva. El nombre reordenamiento es bastante ilustrativo. <br /><br />Ahora, todos sabemos que las sumas son conmutativas, pero reordenar los t\'erminos de una serie es algo totalmente distinto. Un reordenamiento de los t\'erminos de una serie es de la forma<br />$$<br />\sum_{n=1}^\infty a_{\sigma(n)},<br />$$<br />donde $\sigma$ es un reordenamieno de los naturales.<br /><br />{\em {\bf Teorema 1}. Si $\sum a_n$ es absolutamente convergente, entonces los reordenamientos de la serie no afectan el valor de la suma. Es decir, para todo reordenamiento $\sigma$ se tiene<br />$$<br />\sum_{n=1}^\infty a_n = \sum_{n=1}^\infty a_{\sigma(n)}.<br />$$<br />}<br /><br /><br />{\em {\bf Teorema 2 (Riemann)} Supongamos que $a_n$ es condicionalmente convergente. Entonces, para todo n\'umero real $s$, existe un reordenamiento $\sigma$ tal que<br />$$<br />\sum_{n=1}^\infty a_{\sigma(n)} =s<br />$$<br />}<br />$ El desafio entonces es demostrar el teorema 1 y el teorema de Riemann!! ... aunque el primer desafio es entender el teorema de Riemann y sorprenderse como merece tal resultado!

Nico Ver Perfil del Miembro Ver los mensajes de este miembro	Dec 29 2005, 08:39 PM Publicado: #2
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 23 Registrado: 18-May 05 Desde: Paris Miembro Nº: 42	Intentare demostrar el primer teorema... Para poder hacerlo, haré uso de ciertas propiedades que su cumplen y que demostraré de inmediato, para así después poder ocuparlas: 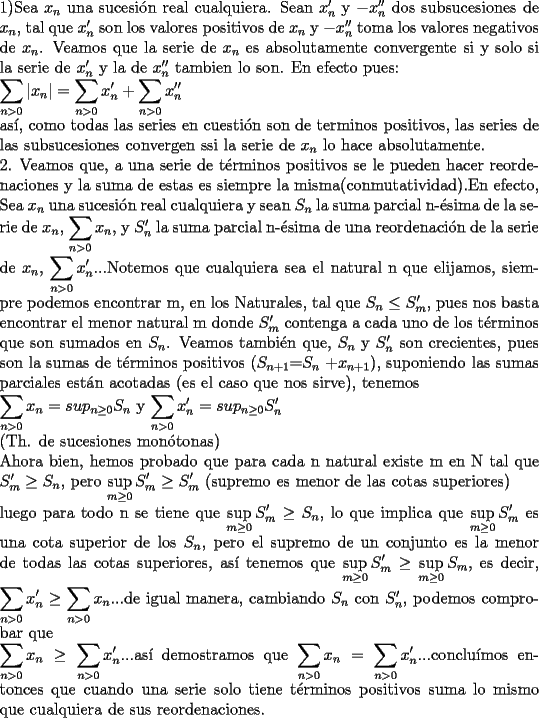$TEX: \noindent <br />1)Sea $x_n$ una sucesi\'on real cualquiera. Sean $x_n^{\prime}$ y $-x_n^{\prime\prime}$ dos subsucesiones de $x_n$, tal que $x_n^{\prime}$ son los valores positivos de $x_n$ y $-x_n^{\prime\prime}$ toma los valores negativos de $x_n$. Veamos que la serie de $x_n$ es absolutamente convergente si y solo si la serie de $x_n^{\prime}$ y la de $x_n^{\prime\prime}$ tambien lo son. En efecto pues:\\<br />$\displaystyle \sum_{n>0}\|x_n\|=\sum_{n>0}x_n^{\prime}+\sum_{n>0}x_n^{\prime\prime}$\\<br />as\'i, como todas las series en cuesti\'on son de terminos positivos, las series de las subsucesiones convergen ssi la serie de $x_n$ lo hace absolutamente.\\<br />2. Veamos que, a una serie de t\'erminos positivos se le pueden hacer reordenaciones y la suma de estas es siempre la misma(conmutatividad).En efecto,\\ <br />Sea $x_n$ una sucesi\'on real cualquiera y sean $S_n$ la suma parcial n-\'esima de la serie de $x_n$, $\displaystyle \sum_{n>0} x_n$, y $S_n^{\prime}$ la suma parcial n-\'esima de una reordenaci\'on de la serie de $x_n$, $\displaystyle \sum_{n>0} x_n^{\prime}$...Notemos que cualquiera sea el natural n que elijamos, siempre podemos encontrar m, en los Naturales, tal que $S_n\le S_m^{\prime}$, pues nos basta encontrar el menor natural m donde $S_m^{\prime}$ contenga a cada uno de los t\'erminos que son sumados en $S_n$. Veamos tambi\'en que, $S_n$ y $S_n^{\prime}$ son crecientes, pues son la sumas de t\'erminos positivos ($S_{n+1}$=$S_n$ +$x_{n+1}$), suponiendo las sumas parciales est\'an acotadas (es el caso que nos sirve), tenemos\\<br />$\displaystyle \sum_{n>0} x_n = sup_{n\ge 0} S_n$ y<br />$\displaystyle \sum_{n>0} x_n^{\prime} = sup_{n\ge 0} S_n^{\prime}$\\<br />(Th. de sucesiones mon\'otonas)\\<br />Ahora bien, hemos probado que para cada n natural existe m en N tal que $S_m^{\prime}\ge S_n$, pero $\displaystyle \sup_{m\ge 0} S_m^{\prime}\ge S_m^{\prime}$ (supremo es menor de las cotas superiores)\\<br />luego para todo n se tiene que $\displaystyle \sup_{m\ge 0} S_m^{\prime}\ge S_n$, lo que implica que $\displaystyle \sup_{m\ge 0} S_m^{\prime}$ es una cota superior de los $S_n$, pero el supremo de un conjunto es la menor de todas las cotas superiores, as\'i tenemos que $\displaystyle \sup_{m\ge 0} S_m^{\prime}\ge \sup_{m\ge 0} S_m$, es decir, $\displaystyle \sum_{n>0} x_n^{\prime}\ge \sum_{n>0} x_n$...de igual manera, cambiando $S_n$ con $S_n^{\prime}$, podemos comprobar que \\<br />$\displaystyle \sum_{n>0} x_n\ge \sum_{n>0} x_n^{\prime}$...as\'i demostramos que $\displaystyle \sum_{n>0} x_n = \sum_{n>0} x_n^{\prime}$...conclu\'imos entonces que cuando una serie solo tiene t\'erminos positivos suma lo mismo que cualquiera de sus reordenaciones.$ $TEX: ...contin\'uo aqu\'i la demostraci\'on...\\<br />Con las dos propiedades antes mostradas, ya podemos demostrar nuestro teorema.\\<br />Veamos que cuando la serie de una sucesi\'on real cualquiera $x_n$ es absolutamente convergente, las subsucesiones, positiva $x_n^{\prime}$ y negativa $-x_n^{\prime\prime}$, convergen(Prop 1) . Sea $\displaystyle \sum_{n>0} y_n$ un reordenamiento de $\displaystyle \sum_{n>0} x_n$, y sean $y_n^{\prime}$ y $-y_n^{\prime\prime}$ subsucesiones de $y_n$, positiva y negativa respectivamente(al decir esto \'ultimo quiero decir que recogen los t'erminos positivos y negativos de $y_n$ ). Veamos que $\displaystyle \sum_{n>0} y_n^{\prime}$ es un reodenamiento de $\displaystyle \sum_{n>0} x_n^{\prime}$ y $\displaystyle \sum_{n>0} y_n^{\prime\prime}$ es un reordenamiento de $\displaystyle \sum_{n>0} x_n^{\prime\prime}$. Notemos tambi\'en, que las cuatro series antes nombradas tienen solo t\'erminos positivos, por lo que (por Prop 2)\\<br />$\displaystyle \sum_{n>0} x_n^{\prime} = \sum_{n>0} y_n^{\prime}$ y$\displaystyle \sum_{n>0} x_n^{\prime\prime} = \sum_{n>0} y_n^{\prime\prime}$... Concluyamos!!\\<br />$\displaystyle \sum_{n>0} x_n=\sum_{n>0} x_n^{\prime} - \sum_{n>0} x_n^{\prime\prime} = \sum_{n>0} y_n^{\prime} - \sum_{n>0} y_n^{\prime\prime} =\sum_{n>0} y_n $...donde \\<br />$\displaystyle \sum_{n>0} y_n$ es un reordenamiento cualquiera...Q.E.D$

Cesarator	Dec 29 2005, 09:19 PM Publicado: #3
Invitado	ok, ideas correctas, demostración correcta... pero la redacción... ay... te sugiero que imprimas tu demostración y la revises en un par de años. En todo caso. Correcto! Falta demostrar el resultado de Riemann

« Posterior · Desafíos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 8th April 2025 - 07:50 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.