|
|
|
|
|
|
|
  |
 Mar 15 2008, 07:47 PM Mar 15 2008, 07:47 PM
Publicado:
#11
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.872 Registrado: 9-March 06 Desde: Welcome Miembro Nº: 614 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
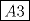 es aplicar el significado de la composicion de funciones. es aplicar el significado de la composicion de funciones.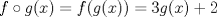 y esto tiene que ser igual a cada parte de la funcion, dependiendo del valor de x. y esto tiene que ser igual a cada parte de la funcion, dependiendo del valor de x.Puedes continuar? Saludos PD: Si te vence la curiosidad... -------------------- USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan
----------------- CURRICULUM VITAE ----------------- 296 pts en la PSU de Matemáticas Admisión 2010. Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica U. de Talca VII Region Chile |
|
|
|
 Mar 15 2008, 07:52 PM Mar 15 2008, 07:52 PM
Publicado:
#12
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
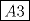 es aplicar el significado de la composicion de funciones. es aplicar el significado de la composicion de funciones.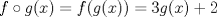 y esto tiene que ser igual a cada parte de la funcion, dependiendo del valor de x. y esto tiene que ser igual a cada parte de la funcion, dependiendo del valor de x.Puedes continuar? Saludos PD: Si te vence la curiosidad... No entendí mucho, pero aer si el concepto es el mismo. Yo pensé que ya que tengo 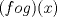 y y 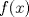 , entonces puedo determinar , entonces puedo determinar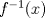 y combinarla con y combinarla con 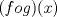 para obtener para obtener 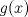 . Esta bien? . Esta bien?
-------------------- |
|
|
|
 Mar 15 2008, 09:47 PM Mar 15 2008, 09:47 PM
Publicado:
#13
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.872 Registrado: 9-March 06 Desde: Welcome Miembro Nº: 614 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
No entendí mucho, pero aer si el concepto es el mismo. Yo pensé que ya que tengo 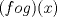 y y 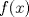 , entonces puedo determinar , entonces puedo determinar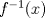 y combinarla con y combinarla con 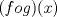 para obtener para obtener 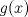 . Esta bien? . Esta bien?Es aplicar la definicion nomas, no hay mucho que entender (bueno, hay que entender la definicion pero si, es lo mismo, gracias a la funcion f(x) que te dieron Saludos -------------------- USA MAPLE ANTES QUE L'HOPITAL!!!! --- fan
----------------- CURRICULUM VITAE ----------------- 296 pts en la PSU de Matemáticas Admisión 2010. Estudiante de Primer Año de Licenciatura en Historia, Ciencias Sociales y Filosofía Jurídica U. de Talca VII Region Chile |
|
|
|
 Mar 16 2008, 03:12 AM Mar 16 2008, 03:12 AM
Publicado:
#14
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 903 Registrado: 28-May 05 Desde: Santiago, Chile Miembro Nº: 69 Nacionalidad:  Colegio/Liceo:  Sexo:  |
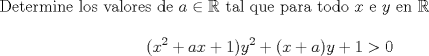 ![TEX: \noindent la expresi\'on equivale a $\left[\left(x+\dfrac{a}{2}\right)y+\dfrac{1}{2}\right]^2+y^2\left(1-\dfrac{a^2}{4}\right)+y\cdot \dfrac{a}{2}+\dfrac{3}{4}$\\<br />\\<br />como $\left[\left(x+\dfrac{a}{2}\right)y+\dfrac{1}{2}\right]^2\ge 0$ , veremos lo que sucede con el resto de la expresi\'on\\<br />\\<br />necesitamos $f(y)=y^2\left(1-\dfrac{a^2}{4}\right)+y\cdot \dfrac{a}{2}+\dfrac{3}{4}>0$ : el coeficiente de $y^2$ no puede ser negativo, pues la funci\'on ser\'ia estrictamente decreciente en el intervalo $[\frac{a}{a^2-4},\infty [$, por lo que existir\'ia $y_0$ tal que $f(y_0)\le 0$ ; ni tampoco puede ser cero, pues $f(y)$ ser\'ia una recta de pendiente $\pm 1$, y claramente existir\'ia $y_0$ tal que $f(y_0)\le 0$\\<br />\\<br />luego, imponemos la condici\'on $1-\dfrac{a^2}{4}>0$ , con lo que $\sqrt{4-a^2}$ est\'a definido en $\mathbb{R}^+$\\<br />\\<br />$f(y)=\left(\dfrac{\sqrt{4-a^2}}{2}y+\dfrac{a}{2\sqrt{4-a^2}}\right)^2+\dfrac{3}{4}-\dfrac{a^2}{4(4-a^2)}$\\<br />\\<br />como $\left(\dfrac{\sqrt{4-a^2}}{2}y+\dfrac{a}{2\sqrt{4-a^2}}\right)^2\ge 0$ , veremos el resto de la expresi\'on\\<br />\\<br />se necesita $\dfrac{3}{4}-\dfrac{a^2}{4(4-a^2)}>0$, lo que se cumple para $-\sqrt{3}<a<\sqrt{3}$\\<br />\\<br />por tanto, el intervalo $]-\sqrt{3},\sqrt{3}[$ es soluci\'on del problema, ya que satisface los valores que debe tomar $a$ para que la expresi\'on inicial sea positiva para cualesquiera $x,y$ reales](./tex/04e2dacd3d000017ab7b503343449b50.png) saludos Mensaje modificado por Guía Rojo el Mar 16 2008, 03:16 AM -------------------- Bachiller en Ciencias
(ex) Estudiante de Medicina Estudiante de Ingeniería Civil de Industrias, diploma en Ingeniería Matemática Pontificia Universidad Católica de Chile  |
|
|
|
 Mar 16 2008, 09:23 PM Mar 16 2008, 09:23 PM
Publicado:
#15
|
|
 Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad:  Colegio/Liceo:  Universidad:  Sexo:  |
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:54 PM |






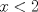 , se necesita que
, se necesita que 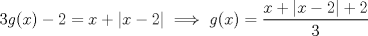
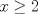 se tiene que
se tiene que 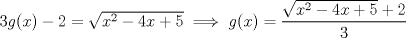
![TEX: \[<br />g(x) = \left\{ {\begin{array}{*{20}c}<br /> {\frac{{x + |x - 2| + 2}}<br />{3}} & {x < 2} \\<br /> {\frac{{\sqrt {x^2 - 4x + 5} }}<br />{3}} & {x \geqslant 2} \\<br /><br /> \end{array} } \right.<br />\]<br />](./tex/4db6f1af1c8da29aa614cc8e149af7b8.png)




![TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]](./tex/e0e88dba678ca3ead120b088f41191b2.png)



![TEX: <br />$ $ \\<br />MAT1503 - Control 1 (A) \\<br />27 de Agosto de 2007 \\<br />$ $ \\<br />$\boxed{A1}$ [2p] Determine los valores de $a \in \mathbb{R}$ tal que para todo $x$ e $y$ en $\mathbb{R}$ \\<br />$$(x^2 + ax +1)y^2 + (x+a)y +1 > 0$$ \\<br />$ $ \\<br />](./tex/6233f0e2ed4f3019ae46b9956345b6cf.png)
![TEX: \noindent Sea $f(y) = (x^2 + ax +1)y^2 + (x+a)y +1$ una función de la forma $f(x)=ax^2+bx+c$, entonces $f(y)>0, \forall y\in\mathbb{R}\iff\triangle_{1}<0$. Mirando $f(y)$ tenemos que<br />\begin{equation*}\begin{aligned}<br />\triangle_{1}&=b^2-4ac\\<br />&=(x+a)^2-4(x^2+ax+1)\cdot 1\\<br />&=x^2+2ax+a^2-4x^2-4ax-4\\<br />\triangle_{1}&=-3x^2-2ax+(a^2-4)\\<br />\end{aligned}\end{equation*}<br />Necesitamos también que $\triangle_{1}<0,\forall x\in\mathbb{R}$ y también se puede observar que puede ser $\triangle_{1}$ puede adoptar la forma de $f(x)=ax^2+bx+c$, con $a<0$, lo que representaría una parábola cuyas ramas se abren hacia abajo. Luego si $\triangle_{2}$ es el discriminante de $f(x)$ tal que $\triangle_{2}<0$ entonces $f(x)=\triangle_{1}<0,\forall x\in\mathbb{R}$.\\<br />Entonces procedemos a analizar $\triangle_{2}$\\<br />\begin{equation*}\begin{aligned}<br />\triangle_{2}&=b^2-4ac\\<br />&=(-2a)^2-4(-3\cdot(a^2-4))\\<br />&=4a^2+12a^2-48\\<br />\triangle_{2}&=16a^2-48\\<br />\end{aligned}\end{equation*}<br />Recordando que para que se cumple la condición $\iff \triangle_{2}<0$<br />\begin{equation*}\begin{aligned}<br />\triangle_{2}=16a^2-48&<0\\<br />a^2-3&<0\\<br />(a^2+\sqrt{3})(a^2-\sqrt{3})&<0\\<br />\Longrightarrow a\in\mathbb{R}&/a\in\{]-\sqrt{3},\sqrt{3}[\} \\<br />\end{aligned}\end{equation*}](./tex/94f922cf316ce9538681db738b3382b3.png)