Segundo Nivel Individual Opciones

[S. E. Puelma Moy...]

Problema 1. En una isla mágica hay 2003 gallinas azules, 1994 gallinas rojas y 1985 gallinas blancas. Las gallinas tienen la siguiente particularidad: si se encuentran dos de distinto color, ambas cambian al tercer color (no existe otro tipo de encuentros). Decida si es posible, luego de algunos cambios, que todas las gallinas queden del mismo color, sea cual sea este color común

Problema 2. Considere un tablero de 4×4; cada casilla puede estar vacía o contener una estrella

1. Pruebe que se pueden colocar siete estrellas, de modo que si se borran dos filas y dos columnas del tablero (cualesquiera), siempre queda al menos una estrella que no fue borrada.
2. Pruebe que lo anterior no es posible si usamos menos estrellas.

[Gp20]

Hola, en la pregunta 1 SI SE PUEDE lograr k las gallinas queden todas del mismo color. Para lograrlo, tomaremos 6 gallinas azules y 6 rojas para encontrarlas. Con esto quedan 1997 gallinas azules, 1988 gallinas rojas y 1997 gallinas blancas. Luego encuentro a las 1997 gallinas azules con las 1997 blancas para que queden 5982 gallinas rojas.

[sí-sí el residen...]

 Dibujo.bmp ( 733.64k ) Número de descargas:  29


En el dibujo podemos ver que si eliminamos dos filas, siempre nos quedan estrellas en 3 columnas distintas, los mismo con las columnas, si elimino dos me quedan estrellas en 3 filas distintas. Con esto nos queda que siempre sobra una estrella.

En el caso de eliminar primero una fila y luego una columna o viceversa, siempre quedan estrellas en 3 filas y dos columnas o 2 columnas y tres filas, aunque puedan estar dos estrelas en una misma fila y columna, sobra una, ya que son 2 y 3 (filas o columnas), por tanto siempre queda almenos una estrella no borrada, y por lo explicado antes, no pueden ser menos que 7.


No se si vera el dibujo

[Chaparrón]

El problema 1 es de la misma forma que la de los camaleones...en fin.
Otra forma para el P1
Viendo los restos de la división por 3 cantidades iniciales se tiene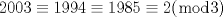

Entonces al ir variando la cantidad de Gallinas, los restos de las tres cantidades siempre
permanecerán iguales, por lo tanto si es posible dejarlas todas de un mismo color.

En conclusión, para ver si es posible dejarlas todas de un mismo color, hay que verificar si se
puede dejar las "n" cantidades divisibles por "n". En este caso las cantidades divisibles por 3 serían
por ejemplo 2001, 1998 y 1983 (haciendo lo de juntar 2 de un colores distintos para que ambas cambien al tercero)

PD: La imagen no se ve. Sólo Me aparece el link para descargarla.
Meeeeeeeeeee

Mensaje modificado por Chaparrón el Dec 29 2007, 06:44 PM