Certamen 1 - Foro fmat.cl

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Concepción > Cálculo IV

Certamen 1, Año 2007

Opciones

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 30 2007, 01:08 PM Publicado: #1
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	Acá subo el certamen, un poquiiito tarde, pero bueno, mas vale tarde que nunca. Hice todo menos la 1-c. Creo que esa solamente la sacó pasten no mas jajaja $TEX: 1- Considere la funci\'on $f(z)=\begin{cases} \dfrac{z+1}{z-1}& \text{si}\,\,\, z\neq 1 \\<br />0&\text{si}\,\,\, z=1\end{cases}$<br /><br />a) Es derivable en $z=1$? Justifique<br /><br />b) Determine el m\'aximo dominio donde $f$ es analitica<br /><br />c) En que figura geom\'etrica trasforma $f$ al eje $y$? 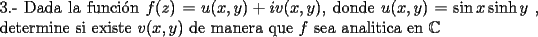Justifique$ *** $TEX: 2.- Pruebe las siguientes identidades:<br /><br />a) $cos(i\overline{z})=\overline{cos(iz)}$<br /><br />b) $sin(z_1+z_2)=sin z_1 cosz_2 + sin z_2 cos z_1$<br /><br />c) $sin \left( \dfrac{\pi}{2}-z \right)=cos z$<br />$ * $TEX: \noindent 3.- Dada la funci\'on $f(z)=u(x,y)+iv(x,y)$, donde $u(x,y)=\sin x \sinh y$ , determine si existe $v(x,y)$ de manera que $f$ sea analitica en $\mathbb{C}$<br />$ * $TEX: \noindent 4.- Determine el mayor subconjunto de $\mathbb{C}$ donde $u(x,y)=Re \left( \dfrac{z}{z^3-1} \right)$ es arm\'onica$ ** $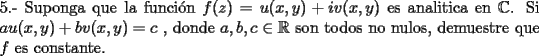TEX: \noindent 5.- Suponga que la funci\'on $f(z)=u(x,y)+iv(x,y)$ es analitica en $\mathbb{C}$. Si $au(x,y)+bv(x,y)=c$ , donde $a,b,c\in \mathbb{R}$ son todos no nulos, demuestre que $f$ es constante.$ **** $TEX: \noindent 6.- Sea $u(x,y)$ una funci\'on arm\'onica en $\mathbb{R}^2$. Muestre que $f(z)=\dfrac{\partial u}{\partial x}(x,y)-i\dfrac{\partial u}{\partial y}(x,y)$ es una funci\'on entera.$