La creatividad a prueba - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Preparación Olimpiadas > Sector Olímpico > Desigualdades > Problemas Resueltos

Reply to this topic

Start new topic

La creatividad a prueba, Resuelto por tebas [medio]

Rurouni Kenshin Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 6 2006, 04:05 AM Publicado: #1
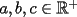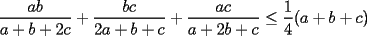Webmaster Grupo: Administrador Mensajes: 6.692 Registrado: 13-May 05 Desde: Santiago Centro Miembro Nº: 2 Nacionalidad: Sexo:	Sean $TEX: $a,b,c\in\mathbb{R}^+$$ . Probar que: $TEX: $\displaystyle \frac{ab}{a+b+2c}+\frac{bc}{2a+b+c}+\frac{ac}{a+2b+c}\le \frac{1}{4}(a+b+c)$$ Mucha suerte -------------------- Colegios/Liceos/Universidades en Fmat (Integrate!!!!) Videos PSU de Funciones (Y tú, ¿Aun estas aproblemado con Funciones?)

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2008, 09:51 PM Publicado: #2
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	Bueno, esta es obviamente una solución fea xD pero quiero ver si aprendí bien o no Muirhead $TEX: \[<br />\begin{gathered}<br /> \frac{1}<br />{4}\left( {a + b + c} \right) \geqslant \frac{{ab}}<br />{{a + b + 2c}} + \frac{{bc}}<br />{{2a + b + c}} + \frac{{ac}}<br />{{a + 2b + c}} \hfill \\<br /> a + b + c - \frac{{4ab}}<br />{{a + b + 2c}} - \frac{{4bc}}<br />{{2a + b + c}} - \frac{{4ac}}<br />{{a + 2b + c}} \geqslant 0 \hfill \\<br /> {\text{Expandimos de forma muy loca obteniendo:}} \hfill \\<br /> \sum\limits_{ciclica} {2a^4 } + \sum\limits_{ciclica} {30a^2 bc} + \sum\limits_{ciclica} {14a^2 b^2 } + \sum\limits_{ciclica} {9a^3 b} - \sum\limits_{ciclica} {8a^3 b} - \sum\limits_{ciclica} {20a^2 b^2 } \hfill \\<br /> - \sum\limits_{ciclica} {28a^2 bc} \geqslant 0 \hfill \\ <br />\end{gathered} <br />\]$ $TEX: \[<br />\begin{gathered}<br /> \sum\limits_{ciclica} {2a^4 } + \sum\limits_{ciclica} {2a^2 bc} + \sum\limits_{ciclica} {a^3 b} \geqslant \sum\limits_{ciclica} {6a^2 b^2 } \hfill \\<br /> \sum\limits_{simetrica} {a^4 } + \sum\limits_{simetrica} {a^2 bc} + \sum\limits_{simetrica} {a^3 b} \geqslant 3\sum\limits_{simetrica} {a^2 b^2 } \hfill \\<br /> {\text{Y esto ultimo es cierto aplicando la desigualdad de Muirhead a los vectores:}} \hfill \\<br /> \left( {{\text{4}}{\text{,0}}{\text{,0}}} \right) \wedge \left( {{\text{2}}{\text{,2}}{\text{,0}}} \right) \hfill \\<br /> \left( {{\text{2}}{\text{,1}}{\text{,1}}} \right) \wedge \left( {{\text{2}}{\text{,2}}{\text{,0}}} \right) \hfill \\<br /> \left( {{\text{3}}{\text{,1}}{\text{,0}}} \right) \wedge \left( {{\text{2}}{\text{,2}}{\text{,0}}} \right) \hfill \\ <br />\end{gathered} <br />\]$ Puedo poner el desarrollo de la expansión si es necesario Me quedan unas dudas; He visto en una solución de Impure y otra The_Lord que ellos colocan como un signo medio raro para denotar las relaciones de orden entre los vectores. ¿Se hace así? --------------------

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2008, 10:20 PM Publicado: #3
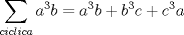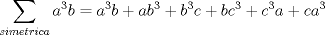Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Bueno tu solución no es correcta; en primer lugar tengo que acotar que $TEX: $\displaystyle\sum_{ciclica}a^3b=a^3b+b^3c+c^3a$$ pero $TEX: $\displaystyle\sum_{simetrica}a^3b=a^3b+ab^3+b^3c+bc^3+c^3a+ca^3$$ ; y además por Muirhead se tiene que $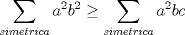TEX: $\displaystyle\sum_{simetrica}a^2b^2 \ge \displaystyle\sum_{simetrica}a^2bc$$ . Así que a seguir intentando no más; tal vez tu solución requiera de una desigualdad más potente que Muirhead, quiza Shür; pero claramente la solución que buscas no es la más creativa, asi que no se talvez buscar otro camino

caf_tito Ver Perfil del Miembro Ver los mensajes de este miembro	Jan 23 2008, 10:28 PM Publicado: #4
Dios Matemático Supremo Grupo: Colaborador Silver Mensajes: 1.605 Registrado: 25-June 05 Miembro Nº: 123 Colegio/Liceo: Universidad: Sexo:	Me equivoqué en llamarla cíclica a la suma entonces Porque efectivamente me refería a $TEX: \[<br />a^3 b + ab^3 + b^3 c + bc^3 + a^3 c + ac^3 <br />\]$ Sin embargo la última correción es cierta, así que a intentar por otro lado --------------------

Luffy Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 12:35 PM Publicado: #5
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 556 Registrado: 16-August 06 Desde: Rio de Janeiro Miembro Nº: 1.950 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	Este problema fue resuelto por tebas en el siguiente Link Saludos

« Posterior · Problemas Resueltos · Anterior »

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Versión Lo-Fi

Fecha y Hora actual: 7th April 2025 - 07:07 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.