Introd. Raz. Matemático (527106) Certamen1-2007 - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Programa Enseñanza Universitaria > Comunidades Universitarias > Universidad de Concepción > Introducción al Razonamiento Matemático

2 Páginas:

1 2 >

Reply to this topic

Start new topic

Introd. Raz. Matemático (527106) Certamen1-2007

Kamelot Ver Perfil del Miembro Ver los mensajes de este miembro	Sep 28 2007, 08:29 PM Publicado: #1
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 165 Registrado: 8-February 06 Desde: Toronto Miembro Nº: 561 Nacionalidad: Universidad: Sexo:	$TEX: \noindent\textbf{1.} Considerar un conjunto $S=\left\{a_1,\ldots,a_n\right\}$ de $n$ elementos y sea $T=\left\{0,1\right\}$. Encontrar una biyecci\'on entre $\mathcal{P}(S)$ (partes de S) y $T^n$ (producto cartesiano de $T$, $n$ veces). Usando lo anterior, demostrar que la cantidad de elementos de $\mathcal{P}(S)$ es $2^n$\\\\\\<br />\textbf{2.} Sea $f:A\to B$ una funci\'on dada. Para $X\subseteq A$ se define $f(X)=\left\{b\in B/\exists a\in X\; tal\; que\; f(a)=b\right\}$. Demostrar que $$X_1,X_2\subseteq A\;\Longrightarrow\;f(X_1)\cap f(X_2)\supseteq f(X_1\cap X_2)$$ Se cumple la igualdad?\\\\\\<br />\textbf{3.} Sean $A$ y $B$ dos conjuntos. Demostrar que $$B-(B-A)=A\;\Longleftrightarrow\; A\subseteq B$$\\ <br />\textbf{4.} Sea $A$ un conjunto no vac\'io. Sea $\rho\subseteq A\times A$ una relaci\'on sobre $A$. Asumir que $\rho$ es sim\'etrica y transitiva. Asumir adem\'as que para cada $a\in A$, existe un elemento $b\in A$ tal que $a\rho b$. Demostrar que $\rho$ es una relaci\'on de equivalencia.$ -------------------- The Little Kitty

cristianyireh Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 2 2007, 11:40 PM Publicado: #2
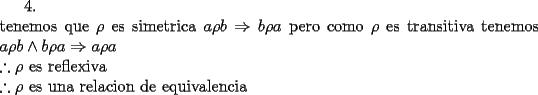Dios Matemático Grupo: Usuario FMAT Mensajes: 216 Registrado: 6-August 07 Desde: concepcion Miembro Nº: 8.270 Nacionalidad: Universidad: Sexo:	$TEX: 4.\\<br />tenemos que $\rho$ es simetrica $a\rho b$ $\Rightarrow b\rho a$ pero como $\rho$ es transitiva tenemos $a\rho b \wedge b \rho a \Rightarrow a\rho a \\ <br />$$\therefore \rho$ es reflexiva $\\<br />\therefore \rho$ es una relacion de equivalencia<br />$ -------------------- nada se compara al placer matematico aunque esquivo vale la pena buscarlo

S. E. Puelma Moy... S. E. Puelma Moya Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 11:02 AM Publicado: #3
Dios Matemático Supremo Grupo: Administrador Mensajes: 2.706 Registrado: 13-May 05 Desde: Santiago de Chile Miembro Nº: 10 Nacionalidad: Colegio/Liceo: Sexo:	Esta respuesta es incorrecta. Una cosa importante, para resolver este tipo de ejercicios, es saber ocupar cuantificadores (hay un cuantificador que "se extraña" por ahí) -------------------- Sebastián Elías Puelma Moya Administrador FMAT

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 11:30 AM Publicado: #4
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	CITA(Kamelot @ Sep 28 2007, 09:29 PM) $TEX: \noindent \textbf{4.} Sea $A$ un conjunto no vac\'io. Sea $\rho\subseteq A\times A$ una relaci\'on sobre $A$. Asumir que $\rho$ es sim\'etrica y transitiva. Asumir adem\'as que para cada $a\in A$, existe un elemento $b\in A$ tal que $a\rho b$. Demostrar que $\rho$ es una relaci\'on de equivalencia.$ $TEX: \noindent Como $(\forall a\in A)(\exists b\in A) a\rho b$ se tiene lo siguiente:<br /><br />\noindent Si $\rho$ es simetrica se tiene que $(\forall a,b\in A)a\rho b\implies b\rho a$<br /><br />\noindent Si $\rho$ es transitiva se tiene que $(\forall a,b,c \in A) [a\rho b \wedge b\rho c] \implies a\rho c$<br /><br />\noindent Si aplicamos la simetria en la transitividad se tiene que:<br /><br />\noindent $(\forall a,b \in A) [a\rho b \wedge b\rho a] \implies a\rho a$<br /><br />\noindent Como se cumple $a\rho a$, entonces $\rho$ es reflexiva.<br /><br />\noindent Como es simetrica, transitiva y reflexiva, $\rho$ es de una relaci\'on de equivalencia.$ salu2

cristianyireh Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 12:52 PM Publicado: #5
Dios Matemático Grupo: Usuario FMAT Mensajes: 216 Registrado: 6-August 07 Desde: concepcion Miembro Nº: 8.270 Nacionalidad: Universidad: Sexo:	CITA(xsebastian @ Oct 3 2007, 08:02 AM) Esta respuesta es incorrecta. Una cosa importante, para resolver este tipo de ejercicios, es saber ocupar cuantificadores (hay un cuantificador que "se extraña" por ahí) si.............reconosco que en mi flojera siempre omito ese tipo de cosas en los post pero la idea de la solucion se sigue como lo hice aunque este ejercicio ya estaba corregido en un certamen anterior ademas jorjeston ya lo posteo mejor Mensaje modificado por cristianyireh el Oct 3 2007, 02:34 PM -------------------- nada se compara al placer matematico aunque esquivo vale la pena buscarlo

Gazoo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 03:04 PM Publicado: #6
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo: Universidad: Sexo:	CITA(jorgeston @ Oct 3 2007, 10:30 AM) $TEX: \noindent Como $(\forall a\in A)(\exists b\in A) a\rho b$ se tiene lo siguiente:<br /><br />\noindent Si $\rho$ es simetrica se tiene que $(\forall a,b\in A)a\rho b\wedge b\rho a$<br /><br />\noindent Si $\rho$ es transitiva se tiene que $(\forall a,b,c \in A) [a\rho b \wedge b\rho c] \implies a\rho c$<br /><br />\noindent Si aplicamos la simetria en la transitividad se tiene que:<br /><br />\noindent $(\forall a,b \in A) [a\rho b \wedge b\rho a] \implies a\rho a$<br /><br />\noindent Como se cumple $a\rho a$, entonces $\rho$ es simetrica.<br /><br />\noindent Como es simetrica, transitiva y reflexiva, $\rho$ es de una relaci\'on de equivalencia.$ salu2 Hay un pequeño error de tipeo, saludos -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein. Estudiante Ingeniería Civil Eléctrica - DIE USACH

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 03:10 PM Publicado: #7
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	CITA(Gazoo @ Oct 3 2007, 04:04 PM) Hay un pequeño error de tipeo, saludos Corregido ( Si es que creo que ese era el error de tipeo) salu2

Gazoo Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 07:46 PM Publicado: #8
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 1.112 Registrado: 21-December 05 Desde: El Bosque - Stgo Miembro Nº: 473 Colegio/Liceo: Universidad: Sexo:	Queda otro error pequeño -------------------- "El sentido común es el conjunto de todos los prejuicios adquiridos antes de los 18 años" A. Einstein. Estudiante Ingeniería Civil Eléctrica - DIE USACH

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 3 2007, 10:27 PM Publicado: #9
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	Ya , está arreglado...

Uchiha Itachi Ver Perfil del Miembro Ver los mensajes de este miembro	Feb 26 2010, 05:04 PM Publicado: #10
Staff FMAT Grupo: Super Moderador Mensajes: 4.857 Registrado: 2-January 08 Miembro Nº: 14.268 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaadaqjEa<br />% qaaiaabofacaqGqbGaaeOmaaaaaeaacaqGobGaae4BaiaabshacaqG<br />% HbGaaeOCaiaabccacaqGXbGaaeyDaiaabwgacaqGGaGaaeiiaiaadI<br />% fadaWgaaWcbaGaaGymaaqabaGccqGHPiYXcaWGybWaaSbaaSqaaiaa<br />% ikdaaeqaaOGaeyOHI0SaamyqaiaabYcacaqGGaGaae4yaiaab+gaca<br />% qGUbGaae4CaiaabMgacaqGKbGaaeyzaiaabkhacaqGLbGaaeyBaiaa<br />% b+gacaqGZbGaaeiiaiaabccacaWGIbGaeyicI4SaamOzamaabmaaba<br />% GaamiwamaaBaaaleaacaaIXaaabeaakiabgMIihlaadIfadaWgaaWc<br />% baGaaGOmaaqabaaakiaawIcacaGLPaaacaqGGaGaaeyzaiaabohaca<br />% qGGaGaaeizaiaabwgacaqGJbGaaeyAaiaabkhacaqGSaGaaeiiaiaa<br />% bwgacaqG4bGaaeyAaiaabohacaqG0bGaaeyzaiaabccacaqGJbGaae<br />% yAaiaabwgacaqGYbGaaeiDaiaab+gacaqGGaGaamyyaiabgIGiolaa<br />% dIfadaWgaaWcbaGaaGymaaqabaGccqGHPiYXcaWGybWaaSbaaSqaai<br />% aaikdaaeqaaaGcbaGaaeiDaiaabggacaqGSbGaaeiiaiaabghacaqG<br />% 1bGaaeyzaiaabccacaqGGaGaamOzamaabmaabaGaamyyaaGaayjkai<br />% aawMcaaiabg2da9iaadkgacaGGUaGaaeiiaiaaboeacaqGVbGaaeyB<br />% aiaab+gacaqGGaGaaeiiaiaadggacqGHiiIZcaWGybWaaSbaaSqaai<br />% aaigdaaeqaaOGaeyykICSaamiwamaaBaaaleaacaaIYaaabeaakiab<br />% gkDiElaadggacqGHiiIZcaWGybWaaSbaaSqaaiaaigdaaeqaaOGaey<br />% 4jIKTaamyyaiabgIGiolaadIfadaWgaaWcbaGaaGOmaaqabaGccaqG<br />% GaGaaeilaiaabccacaqGJbGaae4Baiaab2gacaqGVbGaaeiiaiaabc<br />% cacaWGHbGaeyicI4SaamiwamaaBaaaleaacaaIXaaabeaakiaabcca<br />% caqG5bGaaeiiaiaabshacaqGLbGaaeOBaiaabMgacaqGLbGaaeOBai<br />% aabsgacaqGVbGaaeiiaiaabccacaWGMbWaaeWaaeaacaWGHbaacaGL<br />% OaGaayzkaaGaeyypa0JaamOyaaqaaiaabwgacaqGUbGaaeiDaiaab+<br />% gacaqGUbGaae4yaiaabwgacaqGZbGaaeiiaiaabccacaWGIbGaeyic<br />% I4SaamOzamaabmaabaGaamiwamaaBaaaleaacaaIXaaabeaaaOGaay<br />% jkaiaawMcaaiaac6cacaqGGaGaae4uaiaabMgacaqGNbGaaeyDaiaa<br />% bMgacaqGLbGaaeOBaiaabsgacaqGVbGaaeiiaiaabwgacaqGZbGaae<br />% iDaiaabggacaqGGaGaaeyAaiaabsgacaqGLbGaaeyyaiaabYcacaqG<br />% GaGaae4yaiaab+gacaqGTbGaae4BaiaabccacaWGHbGaeyicI4Saam<br />% iwamaaBaaaleaacaaIYaaabeaakiaabccacaqG5bGaaeiiaiaabcca<br />% caWGMbWaaeWaaeaacaWGHbaacaGLOaGaayzkaaGaeyypa0JaamOyai<br />% aabccacaqGLbGaaeOBaiaabshacaqGVbGaaeOBaiaabogacaqGLbGa<br />% ae4CaiaabccacaWGIbGaeyicI4SaamOzamaabmaabaGaamiwamaaBa<br />% aaleaacaaIYaaabeaaaOGaayjkaiaawMcaaiaab6caaaaa!055E!<br />\[<br />\begin{gathered}<br /> \boxed{{\text{SP2}}} \hfill \\<br /> {\text{Notar que }}X_1 \cap X_2 \subseteq A{\text{, consideremos }}b \in f\left( {X_1 \cap X_2 } \right){\text{ es decir}}{\text{, existe cierto }}a \in X_1 \cap X_2 \hfill \\<br /> {\text{tal que }}f\left( a \right) = b.{\text{ Como }}a \in X_1 \cap X_2 \Rightarrow a \in X_1 \wedge a \in X_2 {\text{ }}{\text{, como }}a \in X_1 {\text{ y teniendo }}f\left( a \right) = b \hfill \\<br /> {\text{entonces }}b \in f\left( {X_1 } \right).{\text{ Siguiendo esta idea}}{\text{, como }}a \in X_2 {\text{ y }}f\left( a \right) = b{\text{ entonces }}b \in f\left( {X_2 } \right){\text{.}} \hfill \\ <br />\end{gathered} <br />\]$ ___________________________________________________________________ $TEX: % MathType!MTEF!2!1!+-<br />% feaagaart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGtb<br />% GaaeyAaiaabccacaqGGaGaaeiiaiaadAgacaqGGaGaaeyzaiaaboha<br />% caqGGaGaaeyAaiaab6gacaqG5bGaaeyzaiaabogacaqG0bGaaeyAai<br />% aabAhacaqGHbGaaeilaiaabccacaqGSbGaaeyyaiaabccacaqGPbGa<br />% ae4zaiaabwhacaqGHbGaaeiBaiaabsgacaqGHbGaaeizaiaabccaca<br />% qGZbGaaeyzaiaabccacaqGJbGaaeyDaiaab2gacaqGWbGaaeiBaiaa<br />% bwgacaqGUaGaaeiiaiaabcfacaqGHbGaaeOCaiaabggacaqGGaGaae<br />% ODaiaabwgacaqGYbGaaeiiaiaabwgacaqGZbGaaeiDaiaabggacaqG<br />% GaGaae4CaiaabMgacaqG0bGaaeyDaiaabggacaqGJbGaaeyAaiaab+<br />% gacaqGUbGaaeilaiaabccacaqGLbGaae4CaiaabccacaqGUbGaaeyz<br />% aiaabogacaqGLbGaae4CaiaabggacaqGYbGaaeyAaiaab+gacaqGGa<br />% GaaeizaiaabwgacaqGTbGaae4BaiaabohacaqG0bGaaeOCaiaabgga<br />% caqGYbGaaeiiaiaabghacaqG1bGaaeyzaaqaaiaadAgadaqadaqaai<br />% aadIfadaWgaaWcbaGaaGymaaqabaaakiaawIcacaGLPaaacqGHPiYX<br />% caWGMbWaaeWaaeaacaWGybWaaSbaaSqaaiaaikdaaeqaaaGccaGLOa<br />% GaayzkaaGaeyOHI0SaamOzamaabmaabaGaamiwamaaBaaaleaacaaI<br />% XaaabeaakiabgMIihlaadIfadaWgaaWcbaGaaGOmaaqabaaakiaawI<br />% cacaGLPaaacaGGUaaabaaabaGaae4uaiaabwgacaqGHbGaaeiiaiaa<br />% bccacaWGIbGaeyicI4SaamOzamaabmaabaGaamiwamaaBaaaleaaca<br />% aIXaaabeaaaOGaayjkaiaawMcaaiabgMIihlaadAgadaqadaqaaiaa<br />% dIfadaWgaaWcbaGaaGOmaaqabaaakiaawIcacaGLPaaacaGGUaaaba<br />% aabaGaae4qaiaab+gacaqGTbGaae4BaiaabccacaWGIbGaeyicI4Sa<br />% amOzamaabmaabaGaamiwamaaBaaaleaacaaIXaaabeaaaOGaayjkai<br />% aawMcaaiabgkDiElaadAgadaqadaqaaiaadggadaWgaaWcbaGaaGym<br />% aaqabaaakiaawIcacaGLPaaacqGH9aqpcaWGIbGaaeiiaiaabccaca<br />% qGJbGaae4Baiaab6gacaqGGaGaaeiiaiaadggadaWgaaWcbaGaaGym<br />% aaqabaGccqGHiiIZcaWGybWaaSbaaSqaaiaaigdaaeqaaOGaaeiiai<br />% aabYcacaqGGaGaaeyyaiaabccacaqGZbGaaeyDaiaabccacaqG2bGa<br />% aeyzaiaabQhacaqGGaGaaeiiaiaadkgacqGHiiIZcaWGMbWaaeWaae<br />% aacaWGybWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaayzkaaGaeyO0<br />% H4TaamOzamaabmaabaGaamyyamaaBaaaleaacaaIYaaabeaaaOGaay<br />% jkaiaawMcaaiabg2da9iaadkgacaqGGaGaaeiiaiaabogacaqGVbGa<br />% aeOBaiaabccacaqGGaGaamyyamaaBaaaleaacaaIYaaabeaakiabgI<br />% GiolaadIfadaWgaaWcbaGaaGOmaaqabaGccaqGUaaabaGaae4uaiaa<br />% bwgacaqGGaGaaeiDaiaabMgacaqGLbGaaeOBaiaabwgacaqGGaGaae<br />% iiaiaadAgadaqadaqaaiaadggadaWgaaWcbaGaaGymaaqabaaakiaa<br />% wIcacaGLPaaacqGH9aqpcaWGMbWaaeWaaeaacaWGHbWaaSbaaSqaai<br />% aaikdaaeqaaaGccaGLOaGaayzkaaGaeyO0H4TaamyyamaaBaaaleaa<br />% caaIXaaabeaakiabg2da9iaadggadaWgaaWcbaGaaGOmaaqabaGcca<br />% qGGaGaaeilaiaabccacaqGWbGaaeyDaiaabwgacaqGZbGaaeiiaiaa<br />% bwgacaqGZbGaaeiiaiaabMgacaqGUbGaaeyEaiaabwgacaqGJbGaae<br />% iDaiaabMgacaqG2bGaaeyyaiaab6cacaqGGaGaaeiraiaabggacaqG<br />% KbGaaeyyaiaabccacaqGLbGaae4CaiaabshacaqGHbGaaeiiaiaabM<br />% gacaqGNbGaaeyDaiaabggacaqGSbGaaeizaiaabggacaqGKbGaaeii<br />% aiaabohacaqGLbGaaeiiaiaabogacaqG1bGaaeyBaiaabchacaqGSb<br />% GaaeyzaiaabccacaqGLbGaaeOBaiaabshacaqGVbGaaeOBaiaaboga<br />% caqGLbGaae4CaaqaaiaabghacaqG1bGaaeyzaiaabccacaqGGaGaam<br />% OyaiabgIGiolaadAgadaqadaqaaiaadIfadaWgaaWcbaGaaGymaaqa<br />% baGccqGHPiYXcaWGybWaaSbaaSqaaiaaikdaaeqaaaGccaGLOaGaay<br />% zkaaGaaeilaiaabccacaqGHbGaae4CaiaabMgacaqGGaGaaeiiaiaa<br />% dAgadaqadaqaaiaadIfadaWgaaWcbaGaaGymaaqabaaakiaawIcaca<br />% GLPaaacqGHPiYXcaWGMbWaaeWaaeaacaWGybWaaSbaaSqaaiaaikda<br />% aeqaaaGccaGLOaGaayzkaaGaeyOHI0SaamOzamaabmaabaGaamiwam<br />% aaBaaaleaacaaIXaaabeaakiabgMIihlaadIfadaWgaaWcbaGaaGOm<br />% aaqabaaakiaawIcacaGLPaaacaGGUaaaaaa!6501!<br />\[<br />\begin{gathered}<br /> {\text{Si }}f{\text{ es inyectiva}}{\text{, la igualdad se cumple}}{\text{. Para ver esta situacion}}{\text{, es necesario demostrar que}} \hfill \\<br /> f\left( {X_1 } \right) \cap f\left( {X_2 } \right) \subseteq f\left( {X_1 \cap X_2 } \right). \hfill \\<br /> \hfill \\<br /> {\text{Sea }}b \in f\left( {X_1 } \right) \cap f\left( {X_2 } \right). \hfill \\<br /> \hfill \\<br /> {\text{Como }}b \in f\left( {X_1 } \right) \Rightarrow f\left( {a_1 } \right) = b{\text{ con }}a_1 \in X_1 {\text{ }}{\text{, a su vez }}b \in f\left( {X_2 } \right) \Rightarrow f\left( {a_2 } \right) = b{\text{ con }}a_2 \in X_2 {\text{.}} \hfill \\<br /> {\text{Se tiene }}f\left( {a_1 } \right) = f\left( {a_2 } \right) \Rightarrow a_1 = a_2 {\text{ }}{\text{, pues es inyectiva}}{\text{. Dada esta igualdad se cumple entonces}} \hfill \\<br /> {\text{que }}b \in f\left( {X_1 \cap X_2 } \right){\text{, asi }}f\left( {X_1 } \right) \cap f\left( {X_2 } \right) \subseteq f\left( {X_1 \cap X_2 } \right). \hfill \\ <br />\end{gathered} <br />\]$ -------------------- Candidato a doctor en Cs. De la ingeniería mención modelamiento matemático, DIM. Universidad de Chile Magíster en ciencias mención matemática, Profesor de estado en matemáticas y computación, Licenciado en educación matemáticas y computación, USACH

« Posterior · Introducción al Razonamiento Matemático · Anterior »

2 Páginas:

1 2 >

Reply to this topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 23rd November 2024 - 05:47 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.