|
|
|
|
|
|
|
  |
 Nov 30 2007, 06:35 PM Nov 30 2007, 06:35 PM
Publicado:
#961
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+c[tex=./tex/error.gif]$u^2$: a,b,c E R}
y considere el operador lineal T: V en V [T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:35 PM Nov 30 2007, 06:35 PM
Publicado:
#962
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+c [tex=./tex/error.gif]$u^2$: a,b,c E R}
y considere el operador lineal T: V en V [T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:35 PM Nov 30 2007, 06:35 PM
Publicado:
#963
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex=./tex/error.gif]$u^2$: a,b,c E R}
y considere el operador lineal T: V en V [T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:36 PM Nov 30 2007, 06:36 PM
Publicado:
#964
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex=./tex/error.gif]$u^2$: a,b,c E R}
y considere el operador lineal T: V en V [T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:38 PM Nov 30 2007, 06:38 PM
Publicado:
#965
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex=./tex/error.gif]$u^2$: a,b,c E R}
y considere el operador lineal T: V en V [T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:39 PM Nov 30 2007, 06:39 PM
Publicado:
#966
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex=./tex/error.gif]$u^2$: a,b,c E R}\ y considere el operador lineal T: V en V
[T(p)](t) = 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:40 PM Nov 30 2007, 06:40 PM
Publicado:
#967
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex]$u^2$: a,b,c E R}\ y considere el operador lineal T: V en V
1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:40 PM Nov 30 2007, 06:40 PM
Publicado:
#968
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+[tex=./tex/error.gif]$u^2$: a,b,c E R} y considere el operador lineal T: V en V [T(p)](t) =
1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:41 PM Nov 30 2007, 06:41 PM
Publicado:
#969
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+cu(u alcuadrado) : a,b,c E R} y considere el operador lineal T: V en V [T(p)](t) =
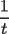 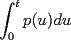 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
 Nov 30 2007, 06:41 PM Nov 30 2007, 06:41 PM
Publicado:
#970
|
|
|
Maestro Matemático Grupo: Usuario FMAT Mensajes: 91 Registrado: 29-October 07 Miembro Nº: 11.960 Nacionalidad:  Sexo:  |
sea V=P2®={p(u)=a+bu+cu(u alcuadrado) : a,b,c E R} y considere el operador lineal T: V en V [T(p)](t) =
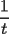 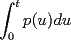 1.1 calcular matriz asociada a T respecto a la base caconica de V 1.2 Es T biyectivo? en caso de serlo, defina defina la inversa de T |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 4th April 2025 - 02:22 PM |








