Probando LaTeX - Foro fmat.cl

437 Páginas:

« < 91 92 93 94 95 > »

Probando LaTeX

Opciones

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 13 2007, 10:25 PM Publicado: #921
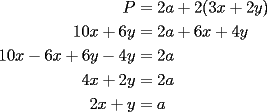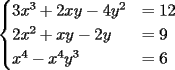Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \begin{equation}<br />\begin{aligned}<br />P &= 2a + 2(3x+2y)\\<br />10x + 6y &= 2a + 6x + 4y\\<br />10x - 6x + 6y - 4y &= 2a\\<br />4x + 2y &=2a\\<br />2x + y &=a<br />\end{aligned}<br />\end{equation}$ $TEX: $\begin{cases}<br />3x^3+2xy-4y^2&=12\\<br />2x^2+xy-2y&=9\\<br />x^4-x^4y^3&=6<br />\end{cases}$<br />$ $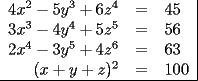TEX: \begin{tabular}{rcl\|}<br />$4x^2-5y^3+6z^4$ & = & $45$ \\<br />$3x^3-4y^4+5z^5$ & = & $56$ \\<br />$2x^4-3y^5+4z^6$ & = & $63$ \\<br />$(x+y+z)^2$ & = & $100$ \\ \hline<br />\end{tabular}$ -------------------- asdf

Black Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 22 2007, 06:09 PM Publicado: #922
Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 26-May 05 Miembro Nº: 62 Nacionalidad: Sexo:	$TEX: f(x)=\frac{x^2-5x+2}{x+2sin(x)}$ $TEX: \sum_{i=1}^{n}\frac{a^{2^i}}{2^{2^i}+1}$

CyedqD Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2007, 04:21 PM Publicado: #923
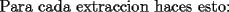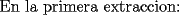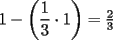Coordinador General Gran Maraton PSU Final 2008 Grupo: Moderador Mensajes: 1.607 Registrado: 11-June 07 Desde: Peñalolen, Stgo Miembro Nº: 6.641 Nacionalidad: Universidad: Sexo:	$TEX: Para cada extraccion haces esto:$ $TEX: Lo que hay $- (\dfrac{1}{3}$ de lo que hay) Siendo esto ultimo lo que se extrae.$ $TEX: En la primera extraccion:$ $TEX: $1 - \left( {\dfrac{1}{3} \cdot 1} \right) = \frac{2}{3}$$ $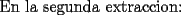TEX: En la segunda extraccion:$ $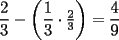TEX: $\dfrac{2}{3} - \left( {\dfrac{1}{3} \cdot \frac{2}{3}} \right) = \dfrac{4}{9}$$ $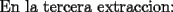TEX: En la tercera extraccion:$ $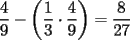TEX: $\dfrac{4}{9} - \left( {\dfrac{1}{3} \cdot \dfrac{4}{9}} \right) = \dfrac{8}{{27}}$$ Mensaje modificado por CyedqD el Nov 23 2007, 04:35 PM --------------------

pelao_malo Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2007, 07:44 PM Publicado: #924
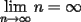
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 878 Registrado: 14-May 07 Desde: Talcahuano Miembro Nº: 5.845 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $\lim\limits_{n\rightarrow \infty}n=\infty$$ Mensaje modificado por pelao_malo el Nov 23 2007, 08:03 PM -------------------- $TEX: $\sqrt{5}=41$$

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 23 2007, 08:23 PM Publicado: #925
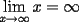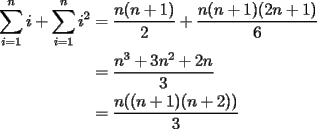Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: $\displaystyle\lim_{x \to \infty}x = \infty$$ $\displaystyle\lim_{x \to \infty}x = \infty$ ----------------------------------------------------------------------------------------------- $TEX: <br />$\begin{aligned}<br />\sum\limits_{i=1}^n{i} + \sum\limits_{i=1}^n{i^2}&= \dfrac{n(n+1)}{2} + \dfrac{n(n+1)(2n+1)}{6} \\ <br />&= \dfrac{n^3+3n^2+2n}{3} \\ <br />&= \dfrac{n((n+1)(n+2))}{3}<br />\end{aligned}$<br />$ $\begin{aligned} \sum\limits_{i=1}^n{i} + \sum\limits_{i=1}^n{i^2}&= \dfrac{n(n+1)}{2} + \dfrac{n(n+1)(2n+1)}{6} \\ &= \dfrac{n^3+3n^2+2n}{3} \\ &= \dfrac{n((n+1)(n+2))}{3} \end{aligned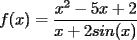}$ ----------------------------------------------------------------------------------------------- $TEX: $f(x)=\dfrac{x^2-5x+2}{x+2sin(x)}$$ $f(x)=\dfrac{x^2-5x+2}{x+2sin(x)}$ Saludos! Sigan probando $TEX: \Huge{\LaTeX}$ ! xD! Mensaje modificado por p.j.t el Nov 25 2007, 10:54 PM -------------------- asdf

mainframe Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 25 2007, 11:03 AM Publicado: #926
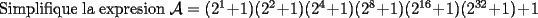
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 23-November 07 Miembro Nº: 12.942 Nacionalidad: Sexo:	test $TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$

Jorgeston Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 25 2007, 04:30 PM Publicado: #927
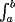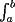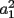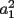
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747	$TEX: $\int_{a}^{b}$$ $TEX: $\int^{b}_{a}$$ $TEX: $a_{1}^{2}$$ $TEX: $a^{2}_{1}$$

Black Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 25 2007, 06:21 PM Publicado: #928
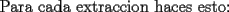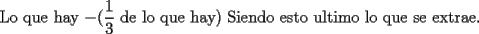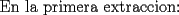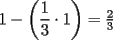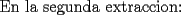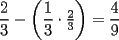Principiante Matemático Grupo: Usuario FMAT Mensajes: 12 Registrado: 26-May 05 Miembro Nº: 62 Nacionalidad: Sexo:	$TEX: Para cada extraccion haces esto:$ $TEX: Lo que hay $- (\dfrac{1}{3}$ de lo que hay) Siendo esto ultimo lo que se extrae.$ $TEX: En la primera extraccion:$ $TEX: $1 - \left( {\dfrac{1}{3} \cdot 1} \right) = \frac{2}{3}$$ $TEX: En la segunda extraccion:$ $TEX: $\dfrac{2}{3} - \left( {\dfrac{1}{3} \cdot \frac{2}{3}} \right) = \dfrac{4}{9}$$ $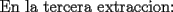TEX: En la tercera extraccion:$ $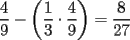TEX: $\dfrac{4}{9} - \left( {\dfrac{1}{3} \cdot \dfrac{4}{9}} \right) = \dfrac{8}{{27}}$$

Fabian+1 Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 26 2007, 03:16 PM Publicado: #929
Maestro Matemático Grupo: Usuario FMAT Mensajes: 88 Registrado: 7-October 07 Desde: La Cisterna Miembro Nº: 11.014 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\aleph_0\daleth_0$$ Mensaje modificado por Fabian+1 el Nov 26 2007, 03:25 PM --------------------

p.j.t Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 26 2007, 03:33 PM Publicado: #930
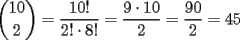Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 766 Registrado: 6-May 07 Desde: San Pedro de la Paz, Concepción Miembro Nº: 5.639 Nacionalidad: Colegio/Liceo: Sexo:	ando ocioso 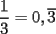$TEX: $\displaystyle{10 \choose 2} = \dfrac{10!}{2!\cdot8!}= \dfrac{9\cdot10}{2}= \dfrac{90}{2}=45$$ $TEX: $\dfrac{1}{3}= 0,\overline{3}$$ PROBANDO.... 1era version $TEX: $2+2=x \Rightarrow (2+2)^2=x^2 \Rightarrow \sqrt[3]{(2+2)^2} = \sqrt[3]{x^2} \Rightarrow \dfrac{\sqrt[3]{(2+2)^2}}{\pi} = \dfrac{\sqrt[3]{x^2}}{\pi} \Rightarrow \Bigg(\dfrac{\sqrt[3]{(2+2)^2}}{\pi}\Bigg)^7 = \Bigg(\dfrac{\sqrt[3]{x^2}}{\pi}\Bigg)^7 \Rightarrow cos\Bigg(\dfrac{\sqrt[3]{(2+2)^2}}{\pi}\Bigg)^7 = cos\Bigg(\dfrac{\sqrt[3]{x^2}}{\pi}\Bigg)^7 \ldots \text{en fin, } x=4$$ PROBANDO.... 2da version $TEX: <br />$\begin{aligned}<br />2+2 &=x \\<br />(3+1)^2 &=x^2 \\<br />\sqrt[3]{(2+2)^2} &= \sqrt[3]{x^2} \\ <br />\dfrac{\sqrt[3]{(2+3-1)^2}}{\pi}& = \dfrac{\sqrt[3]{x^2}}{\pi} \\<br />\Bigg(\dfrac{\sqrt[3]{(2+2)^2}}{\pi}\Bigg)^7 &= \Bigg(\dfrac{\sqrt[3]{x^2}}{\pi}\Bigg)^7 \\<br />cos\Bigg(\dfrac{\sqrt[3]{(2+7-5)^2}}{\pi}\Bigg)^7 &= cos\Bigg(\dfrac{\sqrt[3]{x^2}}{\pi}\Bigg)^7 \\<br />\ldots \\<br />\text{en fin, }\\<br />x=4<br />\end{aligned}$<br />$ $TEX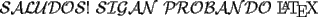: $\mathcal{ANDO\ OCIOSO}$$ $TEX: $\mathcal{SALUDOS}!\ \mathcal{SIGAN\ PROBANDO}$ \LaTeX$ xD -------------------- asdf

437 Páginas:

« < 91 92 93 94 95 > »

23 usuario(s) está(n) leyendo esta discusión (23 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 18th February 2025 - 05:45 PM