Probando LaTeX - Foro fmat.cl

437 Páginas:

« < 386 387 388 389 390 > »

Probando LaTeX

Opciones

frank_ Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 16 2010, 09:34 PM Publicado: #3871
Matemático Grupo: Usuario FMAT Mensajes: 65 Registrado: 17-February 08 Miembro Nº: 15.613 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $M(x)=(200-x) \cdot 60,875-25 \cdot (\dfrac{\pi}{2}-arcsin(\dfrac{x-150}{50})-(\dfrac{x-150}{50}) \cdot <br />cos(arcsin(\dfrac{x-150}{50})) \cdot [ \dfrac{50\cdot(cos(arcsin(\dfrac{x-150}{50}))^3}{3 \cdot (\dfrac{\pi}{2} - <br />arcsin(\dfrac{x-150}{50})-\dfrac{x-150}{50} \cdot cos(arcsin(\dfrac{x-150}{50}))}]$$ Mensaje modificado por frank_ el Oct 16 2010, 09:47 PM

frank_ Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 17 2010, 08:48 PM Publicado: #3872
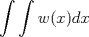
Matemático Grupo: Usuario FMAT Mensajes: 65 Registrado: 17-February 08 Miembro Nº: 15.613 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\displaystyle \int \int w(x)dx$$

profe mate Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 18 2010, 07:53 PM Publicado: #3873
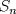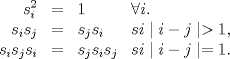
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 20 Registrado: 15-May 08 Desde: Quillota Miembro Nº: 23.186 Nacionalidad: Universidad: Sexo:	Relaciones de los elementos del Grupo de Simetrias $TEX: $S_{n}$$ $TEX: $<br />\begin{array}{rcll}<br />s_{i}^{2} & = & 1 & \forall i. \\<br />s_{i}s_{j} & = & s_{j}s_{i} & si \mid i-j \mid > 1, \\<br />s_{i}s_{j}s_{i} & = & s_{j}s_{i}s_{j} & si \mid i-j \mid = 1.<br />\end{array}<br />$$

heatmove Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 19 2010, 07:05 AM Publicado: #3874
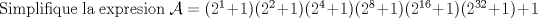
Principiante Matemático Grupo: Usuario FMAT Mensajes: 1 Registrado: 19-October 10 Desde: Santiago Miembro Nº: 78.934 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$

TavoneeT Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 11:36 AM Publicado: #3875
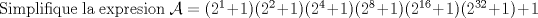
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 1-September 09 Miembro Nº: 58.107	$TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$

TavoneeT Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 11:54 AM Publicado: #3876
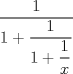
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 1-September 09 Miembro Nº: 58.107	$TEX: $\dfrac{1}{1+\dfrac{1}{1+\dfrac{1}{x}}}$$ Mensaje modificado por TavoneeT el Oct 21 2010, 12:14 PM

TavoneeT Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 21 2010, 12:42 PM Publicado: #3877
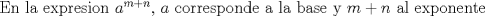
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 1-September 09 Miembro Nº: 58.107	$TEX: En la expresion $a^{m+n}$, $a$ corresponde a la base y $m+n$ al exponente$

Nicolás Javier Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 28 2010, 01:25 PM Publicado: #3878
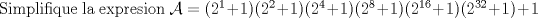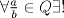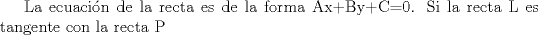Matemático Grupo: Usuario FMAT Mensajes: 38 Registrado: 9-September 10 Desde: La Florida Miembro Nº: 76.958 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$ $TEX: $\forall \frac{a}{b}\in Q \exists!$$ $TEX: La ecuación de la recta es de la forma Ax+By+C=0. 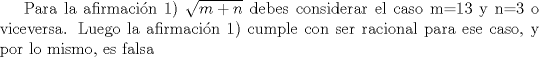Si la recta L es tangente con la recta P$ $TEX: Para la afirmación 1) $\sqrt{m+n}$ debes considerar el caso $m=$13 y $n=$3 o viceversa. 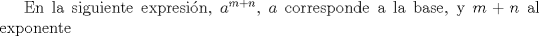Luego la afirmación 1) cumple con ser racional para ese caso, y por lo mismo, es falsa$ $TEX: En la siguiente expresión, $a^{m+n}$, $a$ corresponde a la base, y $m+n$ al exponente$ Mensaje modificado por Nicolás Javier el Oct 28 2010, 06:55 PM -------------------- "Daría todo lo que sé, por la mitad de lo que ignoro" "Si buscas resultados distintos, no hagas siempre lo mismo"

Batero16 Ver Perfil del Miembro Ver los mensajes de este miembro	Oct 29 2010, 12:31 AM Publicado: #3879
Maestro Matemático Grupo: Usuario FMAT Mensajes: 99 Registrado: 10-March 08 Desde: Castro - Chiloé Miembro Nº: 16.544 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	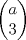$TEX: $$\left ( \begin{matrix}<br /> a \\ <br /> 3 <br />\end{matrix} \right )$$$ Yujuu porfin aprendi a hacer matricez ^^ 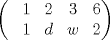$TEX: $$\left ( \begin{matrix}<br /> &1 &2 &3 &6 \\ <br /> &1 &d &w &2 <br />\end{matrix} \right )$$$ JOjojo :=P Mensaje modificado por Batero16 el Oct 29 2010, 12:42 AM

Abu-Khalil Ver Perfil del Miembro Ver los mensajes de este miembro	Nov 1 2010, 12:06 PM Publicado: #3880
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.812 Registrado: 4-November 07 Desde: Santiago Miembro Nº: 12.213 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \noindent Queremos mostrar que <br />\[\int_x^{x+T}f(t)dt=\int_0^Tf(t)dt.\]<br />Todo número real se puede descomponer en un múltiplo de $T$ y algún número pequeño, es decir, existen $k\in\mathbb Z,\xi\in[0,T[$ tales que<br />\[x=kT+\xi.\]<br />Luego, <br />\[\int_x^{x+T}f(t)dt=\int_0^Tf(u+x)du=\int_0^Tf\left((u+\xi)+kT\right)du=\int_0^Tf(u+\xi)du.\]<br />Pero<br />\[<br />\int_0^Tf(u+\xi)du=\int_0^{T-\xi}f(u+\xi)du+\int_{T-\xi}^Tf(u+\xi)du.<br />\]<br />Así, haciendo $z=u+\xi$ en la primera e $y+T=u+\xi$ en la segunda<br />\[\int_0^Tf(u+\xi)du=\int_\xi^Tf(z)dz+\int_0^{\xi}f(y+T)dy=\int_\xi^Tf(z)dz+\int_0^{\xi}f(y)dy=\int_0^Tf(t)dt.\qquad\square\]<br />$ -------------------- ~milopez $TEX: \[\mathfrak{L}=\int_{-\infty}^\infty e^{-289x^2}dx=\frac{\Gamma (\frac{1}{2})}{17}=\frac{\sqrt{\pi}}{17}\]$ $TEX: <br />\begin{equation}\begin{aligned}<br />dS_t&=\mu S_t dt+\sqrt{V_t}S_t dW^S_t\\<br />dV_t&=\kappa(\theta-V_t)dt+\sigma\sqrt{V_t} dW^V_t\\<br />\end{aligned}\end{equation}<br />$ $TEX: <br />$$\mathbb A^{\text U}_M(N)$$<br />$

437 Páginas:

« < 386 387 388 389 390 > »

3 usuario(s) está(n) leyendo esta discusión (3 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 26th November 2024 - 02:24 AM