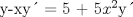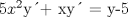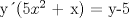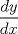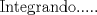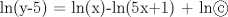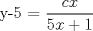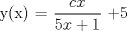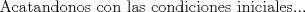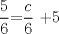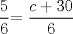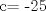Probando LaTeX - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Comunidad Fmat > Sector Manuales

437 Páginas:

« < 279 280 281 282 283 > »

Closed Topic

Start new topic

Probando LaTeX

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:22 PM Publicado: #2801
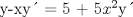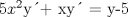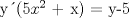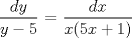Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\displaystyle \frac{dy}{dx}$ = $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x(5x+1)}$$ $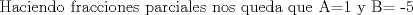TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $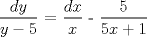TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $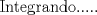TEX: Integrando.....$ $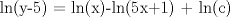TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $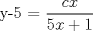TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $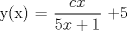TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $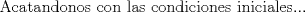TEX: Acatandonos con las condiciones iniciales...$ $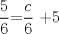TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $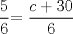TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $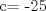TEX: c= -25$ $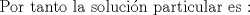TEX: Por tanto la solución particular es :$ $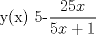TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $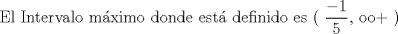TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ [/tex] --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:25 PM Publicado: #2802
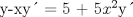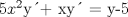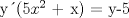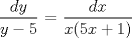Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\displaystyle \frac{dy}{dx}$ = $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x(5x+1)}$$ $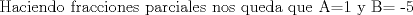TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $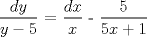TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $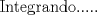TEX: Integrando.....$ $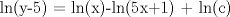TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $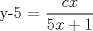TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $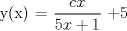TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $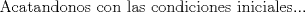TEX: Acatandonos con las condiciones iniciales...$ $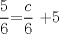TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $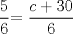TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $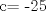TEX: c= -25$ $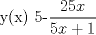TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $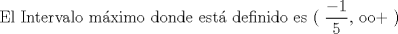TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:27 PM Publicado: #2803
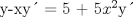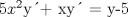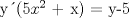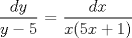Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\displaystyle \frac{dy}{dx}$ = $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $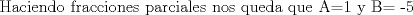TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $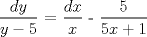TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $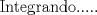TEX: Integrando.....$ $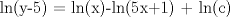TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $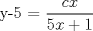TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $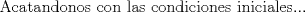TEX: Acatandonos con las condiciones iniciales...$ $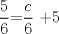TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $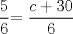TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $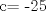TEX: c= -25$ $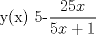TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $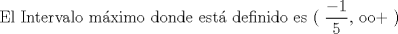TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:29 PM Publicado: #2804
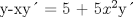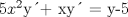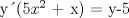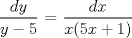Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\displaystyle \frac{dy}{dx}$ = $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $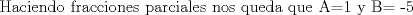TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $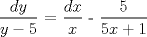TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $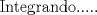TEX: Integrando.....$ $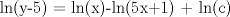TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $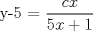TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $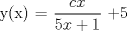TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $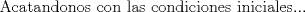TEX: Acatandonos con las condiciones iniciales...$ $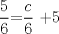TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $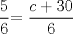TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $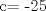TEX: c= -25$ $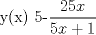TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $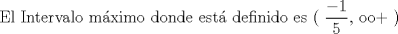TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:31 PM Publicado: #2805
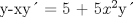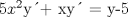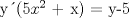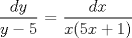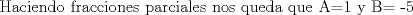Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $y'(x)$ = $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $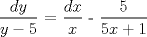TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $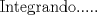TEX: Integrando.....$ $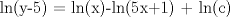TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $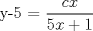TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $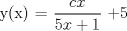TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $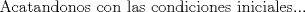TEX: Acatandonos con las condiciones iniciales...$ $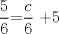TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $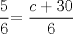TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $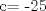TEX: c= -25$ $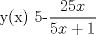TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $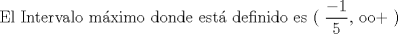TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:32 PM Publicado: #2806
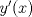
Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: $y'(x)$$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:32 PM Publicado: #2807
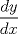
Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: $\dfrac{dy}{dx}$$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:38 PM Publicado: #2808
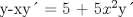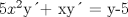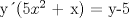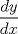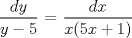Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\dfrac{dy}{dx}$$ $TEX: =$ $TEX: $\displaystyle \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $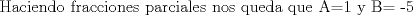TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $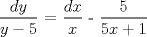TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $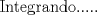TEX: Integrando.....$ $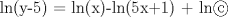TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $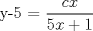TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $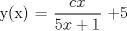TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $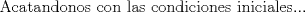TEX: Acatandonos con las condiciones iniciales...$ $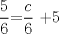TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $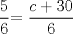TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $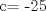TEX: c= -25$ $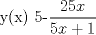TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $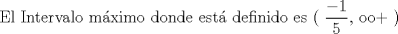TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:41 PM Publicado: #2809
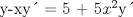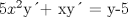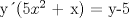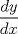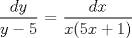Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\dfrac{dy}{dx}$$ $TEX: =$ $TEX: $\dfrac{a}{b}$ \frac{y-5}{ 5$x^{2}$+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $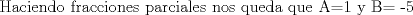TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $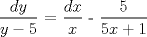TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $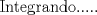TEX: Integrando.....$ $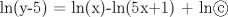TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $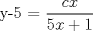TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $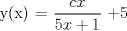TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $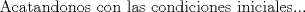TEX: Acatandonos con las condiciones iniciales...$ $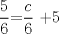TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $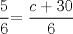TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $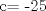TEX: c= -25$ $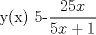TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $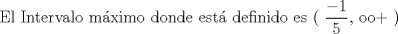TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ --------------------

Danilo_10 Ver Perfil del Miembro Ver los mensajes de este miembro	Apr 2 2009, 08:44 PM Publicado: #2810
Maestro Matemático Grupo: Usuario FMAT Mensajes: 100 Registrado: 21-March 09 Miembro Nº: 45.545 Nacionalidad: Universidad: Sexo:	$TEX: [1] y-xy´ = 5(1+$x^{2}$y´)$ $TEX: y-xy´ = 5 + 5$x^{2}$y´$ $TEX: 5$x^{2}$y´+ xy´ = y-5$ $TEX: y´(5$x^{2}$ + x) = y-5$ $TEX: $\dfrac{dy}{dx}$$ $TEX: =$ $TEX: $\dfrac{a}{b} \frac{y-5}{ 5x^2+x}$$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x (5x+1) }$$ $TEX: Haciendo fracciones parciales nos queda que A=1 y B= -5$ $TEX: $\displaystyle \frac{dy}{y-5}$ = $\displaystyle \frac{dx}{x}$ - $\displaystyle \frac{5}{5x+1}$$ $TEX: Integrando.....$ $TEX: ln(y-5) = ln(x)-ln(5x+1) + ln©$ $TEX: y-5 = $\displaystyle \frac{cx}{5x+1}$$ $TEX: y(x) = $\displaystyle \frac{cx}{5x+1}$ +5$ $TEX: Acatandonos con las condiciones iniciales...$ $TEX: $\displaystyle \frac{5}{6}$=$\displaystyle \frac{c}{6}$ +5$ $TEX: $\displaystyle \frac{5}{6}$= $\displaystyle \frac{c+30}{6}$$ $TEX: c= -25$ $TEX: y(x) 5-$\displaystyle \frac{25x}{5x+1}$$ $TEX: El Intervalo máximo donde está definido es ( $\displaystyle \frac{-1}{5}$, oo+ )$ Archivo(s) Adjunto(s) usachbanneraq5.jpg ( 16.66k ) Número de descargas: 0 --------------------

« Posterior · Sector Manuales · Anterior »

437 Páginas:

« < 279 280 281 282 283 > »

Closed Topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 4th April 2025 - 02:23 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.