Probando LaTeX - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Comunidad Fmat > Sector Manuales

437 Páginas:

« < 235 236 237 238 239 > »

Closed Topic

Start new topic

Probando LaTeX

Andres villegas Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 08:44 PM Publicado: #2361
Maestro Matemático Grupo: Usuario FMAT Mensajes: 115 Registrado: 20-May 08 Miembro Nº: 23.908 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{align}<br /> & P.2 \\ <br /> & \frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ Y }abc=3 \\ <br /> & entonces:\text{ desarrollamos: }\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ }\xrightarrow[{}]{{}}\text{ }\frac{ab^{2}+bc^{2}+ca^{2}}{abc}=1 \\ <br /> & \text{Nos Piden }ab^{2}+bc^{2}+ca^{2}\text{ entonces simplemente reemplazamos el denominador de la fraccion resultante } \\ <br /> & \text{que es }abc=3\text{ porque el enunciado del problema nos da esta informacion}\text{. y simplemente multiplicamos} \\ <br /> & \text{cruzado y obtenemos : } \\ <br /> & \text{ }ab^{2}+bc^{2}+ca^{2}=3\text{ Alternativa A} \\ <br /> & \\ <br /> & \\ <br /> & \\ <br />\end{align}$ -------------------- Estudiante de Segundo Año Universidad Técnica Federico Santa María

Andres villegas Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 08:46 PM Publicado: #2362
Maestro Matemático Grupo: Usuario FMAT Mensajes: 115 Registrado: 20-May 08 Miembro Nº: 23.908 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \begin{align}<br /> & P.2 \\ <br /> & \frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ Y }abc=3 \\ <br /> & entonces:\text{ desarrollamos: }\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ }\xrightarrow[{}]{{}}\text{ }\frac{ab^{2}+bc^{2}+ca^{2}}{abc}=1 \\ <br /> & \text{Nos Piden }ab^{2}+bc^{2}+ca^{2}\text{ entonces simplemente reemplazamos el denominador de la fraccion} \\ <br /> & \text{resultante que es }abc=3\text{ porque el enunciado del problema nos da esta informacion}\text{. } \\ <br /> & \text{y simplemente multiplicamos} \\ <br /> & \text{cruzado y obtenemos : } \\ <br /> & \text{ }ab^{2}+bc^{2}+ca^{2}=3\text{ Alternativa A} \\ <br />\end{align}$ -------------------- Estudiante de Segundo Año Universidad Técnica Federico Santa María

Andres villegas Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 08:47 PM Publicado: #2363
Maestro Matemático Grupo: Usuario FMAT Mensajes: 115 Registrado: 20-May 08 Miembro Nº: 23.908 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	CITA(Andres villegas @ Jul 25 2008, 08:36 PM) $TEX: \begin{align}<br /> P.2 \\ <br /> \frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ Y }abc=3 \\ <br /> entonces:\text{ desarrollamos: }\frac{a}{b}+\frac{b}{c}+\frac{c}{a}=1\text{ }\xrightarrow[{}]{{}}\text{ }\frac{ab^{2}+bc^{2}+ca^{2}}{abc}=1 \\ <br /> \text{Nos Piden }ab^{2}+bc^{2}+ca^{2}\text{ entonces simplemente reemplazamos el denominador de la fraccion} \\ <br /> \text{resultante que es }abc=3\text{ porque el enunciado del problema nos da esta informacion}\text{. } \\ <br /> \text{y simplemente multiplicamos} \\ <br /> \text{cruzado y obtenemos : } \\ <br /> \text{ }ab^{2}+bc^{2}+ca^{2}=3\text{ Alternativa A} \\ <br />\end{align}$ -------------------- Estudiante de Segundo Año Universidad Técnica Federico Santa María

Andres villegas Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 08:50 PM Publicado: #2364
Maestro Matemático Grupo: Usuario FMAT Mensajes: 115 Registrado: 20-May 08 Miembro Nº: 23.908 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\begin{gathered}<br /> \frac{a}<br />{b} + \frac{b}<br />{c} + \frac{c}<br />{a} = 1{\text{ Y }}abc = 3 \hfill \\<br /> entonces:{\text{ desarrollamos: }}\frac{a}<br />{b} + \frac{b}<br />{c} + \frac{c}<br />{a} = 1{\text{ }}\xrightarrow[{}]{{}}{\text{ }}\frac{{ab^2 + bc^2 + ca^2 }}<br />{{abc}} = 1 \hfill \\<br /> {\text{Nos Piden }}ab^2 + bc^2 + ca^2 {\text{ entonces simplemente reemplazamos el denominador de la fraccion}} \hfill \\<br /> {\text{resultante que es }}abc = 3{\text{ porque el enunciado del problema nos da esta informacion}}{\text{. }} \hfill \\<br /> {\text{y simplemente multiplicamos}} \hfill \\<br /> {\text{cruzado y obtenemos : }} \hfill \\<br /> {\text{ }}ab^2 + bc^2 + ca^2 = 3{\text{ Alternativa A}} \hfill \\ <br />\end{gathered} $<br />$ -------------------- Estudiante de Segundo Año Universidad Técnica Federico Santa María

Rob.91 Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 09:32 PM Publicado: #2365
Principiante Matemático Grupo: Usuario FMAT Mensajes: 9 Registrado: 1-June 08 Desde: Afta. Miembro Nº: 25.354 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: [tex]$ 4 $TEX: [/tex]5-4[tex]$ 12 CITA(Black @ Dec 16 2005, 04:45 PM)

Andres villegas Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 25 2008, 09:39 PM Publicado: #2366
Maestro Matemático Grupo: Usuario FMAT Mensajes: 115 Registrado: 20-May 08 Miembro Nº: 23.908 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\begin{gathered}<br /> {\text{Si }}a^3 + 3ab^2 = 63{\text{ y 3}}a^2 b + b^3 = - 62{\text{ }}{\text{, entonces }}\left( \begin{gathered}<br /> \underline {a - b} \hfill \\<br /> a + b \hfill \\ <br />\end{gathered} \right)^3 \hfill \\<br /> {\text{Primero hay que recordar el desarrollo del cubo de Binomio:}} \hfill \\<br /> \left( {a + b} \right)^3 = a^3 + 3a^2 b + 3ab^2 + b^3 \hfill \\<br /> \left( {a - b} \right)^3 = a^3 - 3a^2 b + 3ab^2 - b^3 \hfill \\<br /> Desarrollamos: \hfill \\<br /> \left( \begin{gathered}<br /> \underline {a - b} \hfill \\<br /> a + b \hfill \\ <br />\end{gathered} \right)^3 \xrightarrow[{}]{{}}\frac{{\left( {a - b} \right)^3 }}<br />{{\left( {a + b} \right)^3 }} = \frac{{a^3 - 3a^2 b + 3ab^2 - b^3 }}<br />{{a^3 + 3a^2 b + 3ab^2 + b^3 }} = \hfill \\<br /> \hfill \\<br /> En{\text{ el desarrollo del n\'u merador tomo la expresion 3}}a^2 b + b^3 = - 62{\text{ dada en el enunciado }} \hfill \\<br /> {\text{y se multiplica por - 1}} \hfill \\<br /> {\text{3}}a^2 b + b^3 = - 62{\text{ / - 1 }}\xrightarrow{{}}{\text{ - 3}}a^2 b - b^3 = 62 \hfill \\<br /> \hfill \\<br /> {\text{luego simplemente reemplazamos:}} \hfill \\<br /> \hfill \\<br /> \left( \begin{gathered}<br /> \underline {a - b} \hfill \\<br /> a + b \hfill \\ <br />\end{gathered} \right)^3 \xrightarrow[{}]{{}}\frac{{\left( {a - b} \right)^3 }}<br />{{\left( {a + b} \right)^3 }} = \frac{{a^3 - 3a^2 b + 3ab^2 - b^3 }}<br />{{a^3 + 3a^2 b + 3ab^2 + b^3 }} = \frac{{125}}<br />{1} = 125 \hfill \\<br /> \hfill \\<br /> Alternativa{\text{ B}}{\text{.}} \hfill \\ <br />\end{gathered} $<br />$ -------------------- Estudiante de Segundo Año Universidad Técnica Federico Santa María

johny Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 26 2008, 12:16 AM Publicado: #2367
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 752 Registrado: 15-August 07 Desde: Santiago Miembro Nº: 8.770 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: % MathType!MTEF!2!1!+-<br />% feaafiart1ev1aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn<br />% hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr<br />% 4rNCHbGeaGqiVu0Je9sqqrpepC0xbbL8F4rqqrFfpeea0xe9Lq-Jc9<br />% vqaqpepm0xbba9pwe9Q8fs0-yqaqpepae9pg0FirpepeKkFr0xfr-x<br />% fr-xb9adbaqaaeGaciGaaiaabeqaamaabaabaaGceaqabeaacaqGYa<br />% GaaeioaiaabMcacaqGGaGaaeitaiaabggacaqGGaGaaeyzaiaabIha<br />% caqGWbGaaeOCaiaabwgacaqGZbGaaeyAaiaabopacaqGUbGaaeiiai<br />% aabkdacaqGWaGaaeimaiaabgdadaahaaWcbeqaaiaaikdaaaGccaqG<br />% TaGaaeymaiaabMdacaqG5aGaaeyoaiabgkci3kaabkdacaqGWaGaae<br />% imaiaabgdacaqGRaGaaeyoaiaabMdacaqG5aGaeyOiGCRaaeOmaiaa<br />% bccacaqGLbGaae4CaiaabccacaqGPbGaae4zaiaabwhacaqGHbGaae<br />% iBaiaabccacaqGHbaabaaabaGaaeiuaiaabkhacaqGPbGaaeyBaiaa<br />% bwgacaqGYbGaaeiiaiaabchacaqGHbGaae4Caiaab+gaaeaacaqGYa<br />% GaaeimaiaabcdacaqGXaWaaWbaaSqabeaacaaIYaaaaOGaeyypa0Ja<br />% aGinaiaaicdacaaIWaGaaGinaiaaicdacaaIWaGaaGymaaqaaaqaai<br />% aabofacaqGLbGaae4zaiaabwhacaqGUbGaaeizaiaab+gacaqGGaGa<br />% aeiCaiaabggacaqGZbGaae4BaaqaaiaaisdacaaIWaGaaGimaiaais<br />% dacaaIWaGaaGimaiaaigdacqGHsislcaaIXaGaaGyoaiaaiMdacaaI<br />% 5aGaeyOiGCRaaeOmaiaabcdacaqGWaGaaeymaiaabUcacaqG5aGaae<br />% yoaiaabMdacqGHIaYTcaqGYaaabaGaeyypa0JaaGinaiaaicdacaaI<br />% WaGaaGinaiaaicdacaaIWaGaaGymaiabgkHiTiaaiodacaaI5aGaaG<br />% yoaiaaiMdacaaI5aGaaGyoaiaaiMdacqGHRaWkcaaIXaGaaGyoaiaa<br />% iMdacaaI4aaabaGaeyypa0JaaGOnaiaaicdacaaIWaGaaGimaaqaaa<br />% qaamaaL4babaGaamyqaiaadYgacaWG0bGaamyzaiaadkhacaWGUbGa<br />% amyyaiaadshacaWGPbGaamODaiaadggacaqGGaGaamiraaaaaaaa!AFFC!<br />\[<br />\begin{gathered}<br /> {\text{28) La expresi\'o n 2001}}^2 {\text{ - 1999}} \bullet {\text{2001 + 999}} \bullet {\text{2 es igual a}} \hfill \\<br /> \hfill \\<br /> {\text{Primer paso}} \hfill \\<br /> {\text{2001}}^2 = 4004001 \hfill \\<br /> \hfill \\<br /> {\text{Segundo paso}} \hfill \\<br /> 4004001 - 1999 \bullet {\text{2001 + 999}} \bullet {\text{2}} \hfill \\<br /> = 4004001 - 3999999 + 1998 \hfill \\<br /> = 6000 \hfill \\<br /> \hfill \\<br /> \boxed{Alternativa{\text{ }}D} \hfill \\ <br />\end{gathered} <br />\]<br />$ Mensaje modificado por johny el Jul 26 2008, 12:36 AM

Todo sea por la ... Todo sea por la causa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 26 2008, 01:34 PM Publicado: #2368
Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 7-August 07 Miembro Nº: 8.312 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	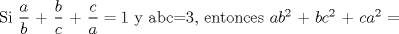$TEX: Si $\displaystyle\frac{a}{b}$ + $\displaystyle\frac{b}{c}$ + $\displaystyle\frac{c}{a}=1$ y abc=3, entonces $ab^2$ + $bc^2$ + $ca^2$ =$ A) 3 B) 2 C) 1 D) 1/3 E) 0 Mensaje modificado por Todo sea por la causa el Jul 26 2008, 01:36 PM -------------------- Llegó el momento de la ansiada despedida :=)

Todo sea por la ... Todo sea por la causa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 26 2008, 01:43 PM Publicado: #2369
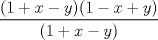
Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 7-August 07 Miembro Nº: 8.312 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: $\displaystyle\frac{(1+x-y)(1-x+y)}{(1+x-y)}$$ Mensaje modificado por Todo sea por la causa el Jul 26 2008, 01:53 PM -------------------- Llegó el momento de la ansiada despedida :=)

Todo sea por la ... Todo sea por la causa Ver Perfil del Miembro Ver los mensajes de este miembro	Jul 26 2008, 01:57 PM Publicado: #2370
Dios Matemático Grupo: Usuario FMAT Mensajes: 270 Registrado: 7-August 07 Miembro Nº: 8.312 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	En una casa comercial hacen un descuento de un 15% de la mitad del precio marcado de una mercadería. Si la mercaderia tiene un precio marcado de $600, ¿Cuánto me descuentan? 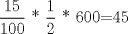$TEX: $\displaystyle\frac{15}{100}$ * $\displaystyle\frac{1}{2}$ * 600=45$ Mensaje modificado por Todo sea por la causa el Jul 26 2008, 03:35 PM -------------------- Llegó el momento de la ansiada despedida :=)

« Posterior · Sector Manuales · Anterior »

437 Páginas:

« < 235 236 237 238 239 > »

Closed Topic

Start new topic

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 25th April 2025 - 11:56 PM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.