Probando LaTeX - Foro fmat.cl

Portal Matemático

¿Qué es FMAT?

Foro fmat.cl > Sector Comunidad Fmat > Sector Manuales

437 Páginas:

« < 189 190 191 192 193 > »

Closed Topic

Start new topic

Probando LaTeX

Fonola Ver Perfil del Miembro Ver los mensajes de este miembro	May 20 2008, 11:10 PM Publicado: #1901
Matemático Grupo: Usuario FMAT Mensajes: 57 Registrado: 14-June 07 Miembro Nº: 6.711 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> {\text{Conservaci\'o n de Momentum:}} \hfill \\<br /> \hfill \\<br /> \overrightarrow p = m\overrightarrow v \hfill \\<br /> \overrightarrow {p_1 } = \overrightarrow {p_2 } \hfill \\<br /> {\text{El Sistema est\'a compuesto por 2 particulas (Carros) A y B}} \hfill \\<br /> \hfill \\<br /> {\text{El Momentum del sistema debe ser igual antes y despues del choque por Ley de Conservaci\'o n de Momentum Lineal}} \hfill \\<br /> \hfill \\<br /> {\text{Antes del choque: }}\overrightarrow {p_1 } = m_1 \overrightarrow {v_1 } + m_2 \overrightarrow {v_2 } \hfill \\<br /> {\text{Despues del Choque: }}\overrightarrow {p_2 } = m_1 \overrightarrow {v_1 '} + m_2 \overrightarrow {v_2 '} \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> {\text{Para el Experimento 1:}} \hfill \\<br /> {\text{Masa A: }}m_1 \hfill \\<br /> {\text{Masa B: }}m_2 \hfill \\<br /> \overrightarrow {v_1 } = 0,5\widehatx\left[ {\frac{m}<br />{s}} \right]{\text{ }}\overrightarrow {v_2 } = 0\widehatx\left[ {\frac{m}<br />{s}} \right] \hfill \\<br /> \overrightarrow {v_1 '} = - 0.1\widehatx\left[ {\frac{m}<br />{s}} \right]{\text{ }}\overrightarrow {v_2 '} = 0.3\widehatx\left[ {\frac{m}<br />{s}} \right] \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> {\text{Para el Experimento 2:}} \hfill \\<br /> {\text{Masa A: }}m_1 + 1\left[ {{\text{kg}}} \right] \hfill \\<br /> {\text{Masa B: }}m_2 \hfill \\<br /> \overrightarrow {v_1 } = 0,5\widehatx\left[ {\frac{m}<br />{s}} \right]{\text{ }}\overrightarrow {v_2 } = 0\widehatx\left[ {\frac{m}<br />{s}} \right] \hfill \\<br /> \overrightarrow {v_1 '} = 0,5\widehatx\left[ {\frac{m}<br />{s}} \right]{\text{ }}\overrightarrow {v_2 '} = 0,5\widehatx\left[ {\frac{m}<br />{s}} \right] \hfill \\ <br />\end{gathered} <br />\]<br />$ $TEX: \[<br />\begin{gathered}<br /> {\text{Desarrollando:}} \hfill \\<br /> \overrightarrow {p_1 } = \overrightarrow {p_2 } \hfill \\<br /> {\text{Experimento 1: }}m_1 \overrightarrow {v_1 } + m_2 \overrightarrow {v_2 } = m_1 \overrightarrow {v_1 '} + m_2 \overrightarrow {v_2 '} \hfill \\<br /> {\text{Experimento 2: (}}m_1 + 1)\overrightarrow {v_1 } + m_2 \overrightarrow {v_2 } = (m_1 + 1)\overrightarrow {v_1 '} + m_2 \overrightarrow {v_2 '} \hfill \\<br /> \hfill \\<br /> \left. {\underline {\, <br /> \begin{gathered}<br /> m_1 \overrightarrow {v_1 } + m_2 \overrightarrow {v_2 } = m_1 \overrightarrow {v_1 '} + m_2 \overrightarrow {v_2 '} \hfill \\<br /> {\text{(}}m_1 + 1)\overrightarrow {v_1 } + m_2 \overrightarrow {v_2 } = (m_1 + 1)\overrightarrow {v_1 '} + m_2 \overrightarrow {v_2 '} \hfill \\ <br />\end{gathered} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> {\text{El resto es la paja de resolver el sistema}}{\text{, pero seguro lo puedes hacer solo}}{\text{.}} \hfill \\<br /> {\text{Tambien}}{\text{, puedes hacerlo sin los 2 experimentos usando conservaci\'o n de la energia}} \hfill \\<br /> {\text{pero claro}}{\text{, tendrias que hacer otro analisis que seguramente no es para tu nivel}}{\text{.}} \hfill \\ <br />\end{gathered} <br />\]<br />$

Fenanov Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2008, 03:16 PM Publicado: #1902
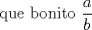
Principiante Matemático Destacado Grupo: Usuario FMAT Mensajes: 19 Registrado: 6-September 07 Miembro Nº: 9.899 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: que bonito $\dfrac{a}{b}$$ -------------------- duffmanboy@Gmail.com

danielomalmsteen Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2008, 03:28 PM Publicado: #1903
Dios Matemático Supremo Grupo: Usuario FMAT Mensajes: 3.413 Registrado: 13-March 08 Desde: Al frente del mundo Magico Miembro Nº: 16.846 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />\[<br />\begin{gathered}<br /> {\text{estoy probando como incorporar texto en el Mathtype}} \hfill \\<br /> \log x = 100 \hfill \\<br /> \hfill \\<br /> \boxed{\left( {a + b} \right)^2 = a^2 + 2ab + b^2 } \hfill \\<br /> \hfill \\<br /> {\text{Me funciono}} \hfill \\<br /> \hfill \\<br /> {\text{xD}} \hfill \\ <br />\end{gathered} <br />\]<br />$ --------------------

liam_gallagher Ver Perfil del Miembro Ver los mensajes de este miembro	May 21 2008, 06:13 PM Publicado: #1904
Dios Matemático Grupo: Usuario FMAT Mensajes: 201 Registrado: 10-September 07 Desde: Las Palmeras Miembro Nº: 10.045 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: <br />$ $TEX: <br />$ Mensaje modificado por liam_gallagher el May 21 2008, 06:18 PM -------------------- Estudiante de tercer año de licenciatura en ciencias con mención en matemáticas - Universidad de Chile

Seguel Ver Perfil del Miembro Ver los mensajes de este miembro	May 22 2008, 11:04 PM Publicado: #1905
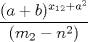Principiante Matemático Grupo: Usuario FMAT Mensajes: 4 Registrado: 2-May 08 Miembro Nº: 21.946 Nacionalidad: Universidad: Sexo:	$TEX: $\displaystyle \frac{(a+b)^{x_{12}+a^2}}{(m_2-n^2)}$$ $TEX: {$\sqrt{1+\sqrt[3]{2+\sqrt[4]{3+\sqrt[5]{4}}}}$$ $TEX: $\displaystyle \lim_{x\rightarrow \infty}\sqrt[n]{3}=1$$ Mensaje modificado por Seguel el May 22 2008, 11:29 PM

Zero c00l Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2008, 12:07 AM Publicado: #1906
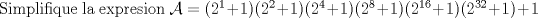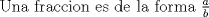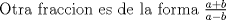
Maestro Matemático Grupo: Usuario FMAT Mensajes: 73 Registrado: 18-May 08 Miembro Nº: 23.529 Nacionalidad: Universidad: Sexo:	$TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$ $TEX: Una fraccion es de la forma $\frac{a}{b}$$ $TEX: Otra fraccion es de la forma $\frac{a+b}{a-b}$$ Mensaje modificado por Zero c00l el May 23 2008, 12:43 PM

josedebajodelmat... josedebajodelmate Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2008, 12:15 AM Publicado: #1907
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 23-October 07 Miembro Nº: 11.675 Nacionalidad: Sexo:	$TEX: \displaystyle \sum_{j=1}^{n}\displaystyle \sum_{i=1}^{j} \displaystyle \sum_{k=0}^{j} \dbinom{i}{k}\displaystyle\ frac{8^{k+1}}{3^î}$$

josedebajodelmat... josedebajodelmate Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2008, 12:15 AM Publicado: #1908
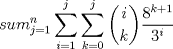
Principiante Matemático Grupo: Usuario FMAT Mensajes: 10 Registrado: 23-October 07 Miembro Nº: 11.675 Nacionalidad: Sexo:	$TEX: $ \displaystyle sum_{j=1}^{n} \sum_{i=1}^{j} \sum_{k=0}^{j} \dbinom{i}{k} \frac {8^{k+1}}{3^i} $$ Mensaje modificado por josedebajodelmate el May 23 2008, 12:33 AM

Xalos Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2008, 05:51 PM Publicado: #1909
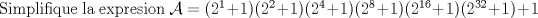Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 7-May 08 Miembro Nº: 22.445 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \noindent Simplifique la expresion $\mathcal{A}=(2^1+1)(2^2+1)(2^4+1)(2^8+1)(2^{16}+1)(2^{32}+1)+1$$

Amaru_Jam Ver Perfil del Miembro Ver los mensajes de este miembro	May 23 2008, 10:23 PM Publicado: #1910
Principiante Matemático Grupo: Usuario FMAT Mensajes: 3 Registrado: 29-March 08 Miembro Nº: 18.379 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \[<br />\begin{gathered}<br /> Sol: \hfill \\<br /> Los{\text{ }}Puntos{\text{ }}son{\text{ }}A( - 3, - 5){\text{ }}y{\text{ }}B(4,16),{\text{ }}entonces{\text{ }}podemos{\text{ }}calcular{\text{ }}su{\text{ }}pendiente \hfill \\<br /> la{\text{ }}cual{\text{ }}es{\text{ }}m{\text{ }} = {\text{ }}\frac{{y_2 - y_1 }}<br />{{x_2 - x_1 }},{\text{ }} \Rightarrow {\text{ }}m{\text{ }} = {\text{ }}\frac{{21}}<br />{7} \Leftrightarrow {\text{ }}m{\text{ }} = {\text{ }}3. \hfill \\<br /> Por{\text{ }}otra{\text{ }}parte{\text{ }}esta{\text{ }}la{\text{ }}ecuacion{\text{ }}de{\text{ }}la{\text{ }}parabola,{\text{ }}la{\text{ }}cual{\text{ }}es{\text{ }}:{\text{ }}y{\text{ }} = {\text{ }}\frac{{x^2 + 4x - 8}}<br />{4} \hfill \\<br /> Y{\text{ }}nos{\text{ }}piden{\text{ }}que{\text{ }}calculemos{\text{ }}la{\text{ }}ecuacaion{\text{ }}de{\text{ }}la{\text{ }}recta{\text{ }}L,{\text{ }}si{\text{ }}esta{\text{ }}es{\text{ }}perdendicular{\text{ }}a{\text{ }}la{\text{ }}recta{\text{ }}\overrightarrow {AB} {\text{ }}y{\text{ }}que{\text{ }}pase{\text{ }}por{\text{ }}el{\text{ }}vertice{\text{ }}de{\text{ }}la{\text{ }}parabola. \hfill \\<br /> Desarrollemoslo: \hfill \\<br /> Como{\text{ }}son{\text{ }}perpendiculares,{\text{ }}entonces{\text{ }}m_1 \bullet m_{2{\text{ }}} = {\text{ }} - 1{\text{ }} \Rightarrow {\text{ }}3 \bullet m_{2{\text{ }}} = {\text{ }} - 1,{\text{ }}\therefore m_{2{\text{ }}} = {\text{ }}\frac{{ - 1}}<br />{3}{\text{ }} \hfill \\<br /> Despues{\text{ }}tenemos{\text{ }}que{\text{ }}calcular{\text{ }}el{\text{ }}vertice{\text{ }}de{\text{ }}la{\text{ }}parabola,{\text{ }}la{\text{ }}cual{\text{ }}es: \hfill \\<br /> V{\text{ }} = {\text{ }}\left( {\frac{{ - b}}<br />{{2a}},\frac{{4ac - b^2 }}<br />{{4a}}} \right){\text{ }},{\text{ }}reemplazamos{\text{ }}y{\text{ }}tenemos{\text{ }}que{\text{ }}V{\text{ }} = {\text{ }}\left( { - 2, - 3} \right) \hfill \\<br /> Ahora{\text{ }}recordemos{\text{ }}se{\text{ }}puede{\text{ }}escribir{\text{ }}la{\text{ }}ecuacion{\text{ }}de{\text{ }}una{\text{ }}recta{\text{ }}si{\text{ }}conocemos{\text{ }}su{\text{ }}pendiente{\text{ }}y{\text{ }}2{\text{ }}de{\text{ }}sus{\text{ }}puntos. \hfill \\<br /> La{\text{ }}ecuacion{\text{ }}general{\text{ }}de{\text{ }}una{\text{ }}recta{\text{ }}es{\text{ }}:{\text{ }}y{\text{ }} - y_{1{\text{ }}} = {\text{ }}m\left( {x - x_1 } \right),{\text{ }}entonces{\text{ }}tenemos{\text{ }}que: \hfill \\<br /> y{\text{ }} + {\text{ }}3{\text{ }} = {\text{ }}\frac{{ - 1}}<br />{3}\left( {x{\text{ }} + 2} \right),{\text{ }}\therefore {\text{ }}esta{\text{ }}es{\text{ }}la{\text{ }}ecuacion{\text{ }}de{\text{ }}la{\text{ }}recta{\text{ }}pedida. \hfill \\<br /> \hfill \\ <br />\end{gathered} <br />\]<br />$

« Posterior · Sector Manuales · Anterior »

437 Páginas:

« < 189 190 191 192 193 > »

Closed Topic

Start new topic

2 usuario(s) está(n) leyendo esta discusión (2 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Suscribirse · Enviar por correo · Imprimir · Suscribirse a este foro

Versión Lo-Fi

Fecha y Hora actual: 21st April 2025 - 05:41 AM

Powered By IP.Board 2.2.1 © 2007 IPS, Inc.