Probando LaTeX - Foro fmat.cl

437 Páginas:

« < 182 183 184 185 186 > »

Probando LaTeX

Opciones

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 01:31 PM Publicado: #1831
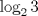
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: $$<br />\log _2 3<br />$$$

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 01:34 PM Publicado: #1832
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: $\root 3 \of {72 - 32\sqrt 5 } = x - \sqrt y ...............(1)$<br />$\root 3 \of {72 + 32\sqrt 5 } = x + \sqrt y ...............(2)$<br />Multiplicamos (1)(2) y tenemos <br /><br />$\root 3 \of {(72 - 32\sqrt 5 )(72 + 32\sqrt 5 )} = (x - \sqrt y )(x + \sqrt y )$<br />$\Leftrightarrow \root 3 \of {5184 - 10245} = x^2 - y$<br />$\Leftrightarrow \root 3 \of {5184 - 5120} = x^2 - y$<br />$\Leftrightarrow \root 3 \of {64} = x^2 - y$<br />$\Leftrightarrow 4 = x^2 - y$<br />$\Leftrightarrow y = x^2 - 4.........................(3)$<br /><br /><br /><br />por otra parte<br /><br />$\root 3 \of {72 - 32\sqrt 5 } = x - \sqrt y /()^3$<br />$\Leftrightarrow 72 - 32\sqrt 5 = x^3 - 3x^2 \sqrt y + 3xy - y\sqrt y$<br /><br /><br />Igualemos las cantidades racionales<br /><br />$72 = x^3 + 3xy........................(4)$<br />Ahora bien reemplacemos (3) en (4)<br /><br />$72 = x^3 + 3x(x^2 - 4)$<br />Simplificando y reduciendo tenemos <br /><br />$x^3 - 3x = 18$<br /><br />Por tanteos hallamos que $x = 3$<br />Al reemplazar x en (3)<br />tenemos que y=5<br /><br /><br />Y como la expresión tiene la forma de $x-\sqrt{y}$<br />la raíz cúbica de la expresión será<br />$3-\sqrt{5}$$ Mensaje modificado por vivanco el May 3 2008, 02:20 PM

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 02:44 PM Publicado: #1833
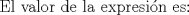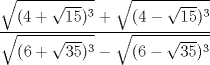
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: El valor de la expresión es:$ $TEX: $$\frac{{\sqrt {(4 + \sqrt {15} )^3 } ^{} + \sqrt {(4 - \sqrt {15} )^3 } }}<br />{{\sqrt {(6 + \sqrt {35} )^3 } - \sqrt {(6 - \sqrt {35} )^3 } }}$$$ Mensaje modificado por vivanco el May 3 2008, 02:51 PM

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 02:54 PM Publicado: #1834
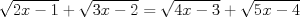
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: $$<br />\sqrt {2x - 1} + \sqrt {3x - 2} = \sqrt {4x - 3} + \sqrt {5x - 4} <br />$$$

gerardo 18 Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 04:50 PM Publicado: #1835
Matemático Grupo: Usuario FMAT Mensajes: 69 Registrado: 13-March 08 Miembro Nº: 16.848 Nacionalidad: Colegio/Liceo: Sexo:	$TEX: \[<br />\frac{{ - b \pm \sqrt {b^2 - 4ac} }}<br />{{2a}}<br />\]<br />$ probando :B

angelita Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 07:55 PM Publicado: #1836
Dios Matemático Grupo: Usuario FMAT Mensajes: 363 Registrado: 12-October 06 Miembro Nº: 2.478 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> 5) \hfill \\<br /> \hfill \\<br /> \vartriangle CAB \cong \vartriangle DAB \to \overline {CA} \cong \overline {DA} \hfill \\<br /> {\text{ }}\overline {CB} \cong \overline {DB} \hfill \\<br /> \hfill \\<br /> \overline {DA} = 3 \hfill \\<br /> \overline {CA} = x + 2 = 3\therefore \left. {\underline {\, <br /> {x = 1} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> \overline {DB} \cong {\text{ }}\overline {CB} \to x + 1 = y - 4 \hfill \\<br /> {\text{ }}1 + 1 = y - 4 \to \left. {\underline {\, <br /> {y = 6} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> \therefore y - x = 5 \hfill \\<br /> \hfill \\<br /> {\text{Alternativa B}} \hfill \\ <br />\end{gathered} <br />\]<br />$

angelita Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 07:56 PM Publicado: #1837
Dios Matemático Grupo: Usuario FMAT Mensajes: 363 Registrado: 12-October 06 Miembro Nº: 2.478 Nacionalidad: Colegio/Liceo: Universidad: Sexo:	$TEX: \[<br />\begin{gathered}<br /> 5) \hfill \\<br /> \hfill \\<br /> \vartriangle CAB \cong \vartriangle DAB \to \overline {CA} \cong \overline {DA} \hfill \\<br /> {\text{ }}\overline {CB} \cong \overline {DB} \hfill \\<br /> \hfill \\<br /> \overline {DA} = 3 \hfill \\<br /> \overline {CA} = x + 2 = 3\therefore \left. {\underline {\, <br /> {x = 1} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> \overline {DB} \cong {\text{ }}\overline {CB} \to x + 1 = y - 4 \hfill \\<br /> {\text{ }}1 + 1 = y - 4 \to \left. {\underline {\, <br /> {y = 6} \,}}\! \right\| \hfill \\<br /> \hfill \\<br /> \therefore y - x = 5 \hfill \\<br /> \hfill \\<br /> {\text{Alternativa B}} \hfill \\ <br />\end{gathered} <br />\]<br />$ Archivo(s) Adjunto(s) problema5.JPG ( 8.7k ) Número de descargas: 1 problema5.JPG ( 8.7k ) Número de descargas: 0

Phi Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 08:12 PM Publicado: #1838
Doctor en Matemáticas Grupo: Usuario FMAT Mensajes: 161 Registrado: 11-October 07 Miembro Nº: 11.187 Nacionalidad: Sexo:	$TEX: <br />F^2<br />$ Mensaje modificado por Phi el May 3 2008, 08:22 PM --------------------

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 3 2008, 11:55 PM Publicado: #1839
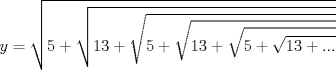
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: $$<br />y = \sqrt {5 + \sqrt {13 + \sqrt {5 + \sqrt {13 + \sqrt {5 + \sqrt {13 + ...} } } } } } <br />$$$

xdanielx Ver Perfil del Miembro Ver los mensajes de este miembro	May 4 2008, 12:45 AM Publicado: #1840
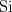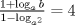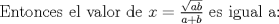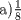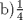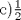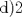
Dios Matemático Supremo Grupo: Baneado Mensajes: 3.360 Registrado: 11-March 08 Miembro Nº: 16.617	$TEX: Si$ $TEX: $\frac{{1 + \log _a b}}{{1 - \log _{a^2 } }} = 4$$ $TEX: Entonces el valor de<br />$x = \frac{{\sqrt {ab} }}{{a + b}}$ es igual a:$ $TEX: a)$\frac{1}{8}$$ $TEX: b)$\frac{1}{4}$$ $TEX: c)$\frac{1}{2}$$ $TEX: d)2$ $TEX: e)1$

437 Páginas:

« < 182 183 184 185 186 > »

1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))

0 miembro(s):

Modo de Ver: Estándar · Cambiar a: Lineal+ · Cambiar a: Outline

Fecha y Hora actual: 21st April 2025 - 03:44 PM