|
|
|
|
|
|
|
  |
 Sep 7 2007, 08:22 PM Sep 7 2007, 08:22 PM
Publicado:
#1
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
Acá dejo el certamen del año pasado, bastante facil en realidad. Ojalá nos toque uno asi este lunes
P1 Resuelva los siguienes ejercicios, fundamentando su respuesta ( 0,5 ptos cada uno): a) Dada la funcion de ecuacion 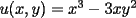 , determine la funcion armonica conjugada de , determine la funcion armonica conjugada de  b) Sea 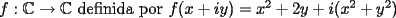 . Determine los puntos del plano complejo . Determine los puntos del plano complejo 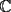 donde donde 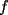 es derivable. es derivable.c) Dada la funcion : 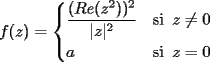 Determine, si existe, el valor de  de manera que de manera que 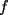 sea continua en sea continua en 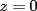 **** P2 Haga ver que (0,5 ptos cada uno): a) 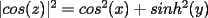 , donde , donde 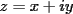 b) 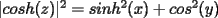 , donde , donde 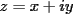 c) Si 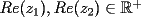 entonces entonces 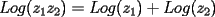 **** P3 (1,5 ptos) Suponga que 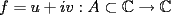 es una funcion analitica en su dominio. Muestre que si es una funcion analitica en su dominio. Muestre que si 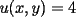 , , 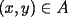 , entonces , entonces 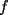 es constante. es constante.**** P4 (1,5 ptos) Suponga que 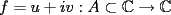 es una funcion analitica en su dominio y que sus funciones componentes sn de clase es una funcion analitica en su dominio y que sus funciones componentes sn de clase 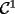 en en 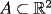 . Se define . Se define 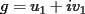 donde donde 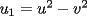 y y 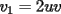 . Se afirma que . Se afirma que 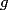 es analitica en es analitica en 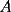 ¿Es verdadera la informacion?, justifique su respuesta. |
|
|
|
 Sep 8 2007, 12:29 AM Sep 8 2007, 12:29 AM
Publicado:
#2
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
P1
a) Sea  la función a buscar. la función a buscar. saludos |
|
|
|
 Sep 8 2007, 12:39 AM Sep 8 2007, 12:39 AM
Publicado:
#3
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
P1
b) 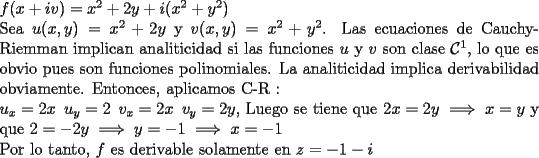 salu2! |
|
|
|
 Sep 8 2007, 12:53 AM Sep 8 2007, 12:53 AM
Publicado:
#4
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
P1
c) 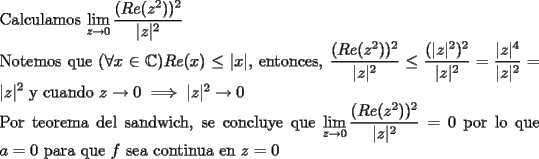 salu2 |
|
|
|
 Sep 8 2007, 01:00 AM Sep 8 2007, 01:00 AM
Publicado:
#5
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
|
|
|
|
 Sep 9 2007, 03:12 PM Sep 9 2007, 03:12 PM
Publicado:
#6
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
|
|
|
|
 Sep 9 2007, 04:13 PM Sep 9 2007, 04:13 PM
Publicado:
#7
|
|
|
Dios Matemático Supremo Grupo: Baneado Mensajes: 2.588 Registrado: 7-November 06 Miembro Nº: 2.747 |
|
|
|
|
 Jan 29 2009, 11:08 AM Jan 29 2009, 11:08 AM
Publicado:
#8
|
|
 Dios Matemático Supremo Grupo: Super Moderador Mensajes: 1.912 Registrado: 10-January 08 Desde: Un Sobolev Miembro Nº: 14.530 Nacionalidad:  Sexo:  |
-------------------- |
|
|
|
  |
1 usuario(s) está(n) leyendo esta discusión (1 invitado(s) y 0 usuario(s) anónimo(s))
0 miembro(s):
| Versión Lo-Fi | Fecha y Hora actual: 25th April 2025 - 11:52 PM |












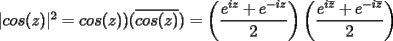

![TEX: \noindent Sean $z_1=x_1+iy_1$, $z_2=x_2+iy_2$, con $x_1,x_2>0$, lo que implica que $\Theta=\mathrm{Arg}\,z_1\in\,\left]-\dfrac{\pi}{2},\dfrac{\pi}{2}\right[$ y que $\Phi=\mathrm{Arg}\,z_2\in\,\left]-\dfrac{\pi}{2},\dfrac{\pi}{2}\right[$. (*)\\<br />Además, si $r_1$ y $r_2$ respresentan los módulos de $z_1$ y $z_2$, respectivamente, se tiene:<br />$$\log(z_1z_2)=\log(r_1r_2\exp(\Theta +\Phi))=\ln(r_1r_2)+i(\Theta + \Phi)$$<br /><br />\noindent Por (*), se tiene que el ángulo $\Gamma=(\Theta +\Phi)\in\,]-\pi,\pi[$, por lo que estamos frente al valor principal del logartimo y así, podemos escribir:<br />$$\mathrm{Log}\,(z_1z_2)=\ln(r_1r_2)+i\Gamma,\textrm{ con $-\pi<\Gamma<\pi$}$$<br /><br />\noindent Ahora bien:<br />\begin{align}<br />\mathrm{Log}\,(z_1)=\ln r_1+i\Theta,\quad-\dfrac{\pi}{2}<\Theta<\dfrac{\pi}{2}\\<br />\mathrm{Log}\,(z_2)=\ln r_2+i\Phi,\quad-\dfrac{\pi}{2}<\Phi<\dfrac{\pi}{2}<br />\end{align}<br />\noindent Luego, usando las propiedades del logartimo real:<br />\begin{align*}<br />\mathrm{Log}\,(z_1)+\mathrm{Log}\,(z_2)&=\ln r_1+i\Theta + \ln r_2+i\Phi\\<br />&=\ln(r_1r_2)+i(\Theta +\Phi)\\<br />&=\ln(r_1r_2)+i\Gamma,\textrm{ con $-\pi<\Gamma<\pi$} <br />\end{align*}<br />de donde se concluye lo pedido.<br />](./tex/7deeb1c77c461f2afababd9946c7ba17.png)
